Lab 2a: Tuning Support Vector Machines

Support Vector Machines are powerful methods, but they also require careful tuning. We’ll explore SVM kernels and hyperparameters on an artificial dataset. We’ll especially look at model underfitting and overfitting.

# Auto-setup when running on Google Colab
if 'google.colab' in str(get_ipython()):
    !pip install openml

# General imports
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import openml as oml
from matplotlib import cm

# Hide convergence warning for now
import warnings
from sklearn.exceptions import ConvergenceWarning
warnings.filterwarnings("ignore", category=ConvergenceWarning)

# Hiding all warnings. Not recommended, just for compilation.
if not sys.warnoptions:
    warnings.simplefilter("ignore")
    os.environ["PYTHONWARNINGS"] = "ignore"

Getting the data

We fetch the Banana data from OpenML: https://www.openml.org/d/1460

bananas = oml.datasets.get_dataset(1460) # Banana data has OpenML ID 1460
X, y, _, _ = bananas.get_data(target=bananas.default_target_attribute, dataset_format='array');

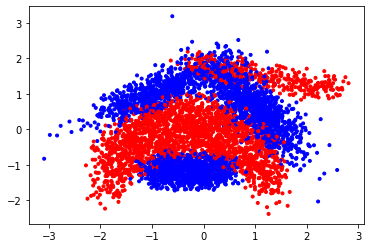
Quick look at the data:

plt.scatter(X[:,0], X[:,1], c=y,cmap=plt.cm.bwr, marker='.');

# Plotting helpers. Based loosely on https://github.com/amueller/mglearn
def plot_svm_kernel(X, y, title, support_vectors, decision_function, dual_coef=None, show=True):
    """
    Visualizes the SVM model given the various outputs. It plots:
    * All the data point, color coded by class: blue or red
    * The support vectors, indicated by circling the points with a black border. 
      If the dual coefficients are known (only for kernel SVMs) if paints support vectors with high coefficients darker
    * The decision function as a blue-to-red gradient. It is white where the decision function is near 0.
    * The decision boundary as a full line, and the SVM margins (-1 and +1 values) as a dashed line
    
    Attributes:
    X -- The training data
    y -- The correct labels
    title -- The plot title
    support_vectors -- the list of the coordinates of the support vectores
    decision_function - The decision function returned by the SVM
    dual_coef -- The dual coefficients of all the support vectors (not relevant for LinearSVM)
    show -- whether to plot the figure already or not
    """
    # plot the line, the points, and the nearest vectors to the plane
    #plt.figure(fignum, figsize=(5, 5))
    plt.title(title)
    plt.scatter(X[:, 0], X[:, 1], c=y, zorder=10, cmap=plt.cm.bwr, marker='.')
    if dual_coef is not None:
        plt.scatter(support_vectors[:, 0], support_vectors[:, 1], c=dual_coef[0, :],
                    s=70, edgecolors='k', zorder=10, marker='.', cmap=plt.cm.bwr)
    else:
        plt.scatter(support_vectors[:, 0], support_vectors[:, 1], facecolors='none',
                    s=70, edgecolors='k', zorder=10, marker='.', cmap=plt.cm.bwr)
    plt.axis('tight')
    x_min, x_max = -3.5, 3.5
    y_min, y_max = -3.5, 3.5

    XX, YY = np.mgrid[x_min:x_max:300j, y_min:y_max:300j]
    Z = decision_function(np.c_[XX.ravel(), YY.ravel()])

    # Put the result into a color plot
    Z = Z.reshape(XX.shape)
    plt.contour(XX, YY, Z, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'],
                levels=[-1, 0, 1])
    plt.pcolormesh(XX, YY, Z, vmin=-1, vmax=1, cmap=plt.cm.bwr, alpha=0.1)

    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)
    
    plt.xticks(())
    plt.yticks(())

    if show:
        plt.show()
    
def heatmap(values, xlabel, ylabel, xticklabels, yticklabels, cmap=None,
            vmin=None, vmax=None, ax=None, fmt="%0.2f"):
    """
    Visualizes the results of a grid search with two hyperparameters as a heatmap.
    Attributes:
    values -- The test scores
    xlabel -- The name of hyperparameter 1
    ylabel -- The name of hyperparameter 2
    xticklabels -- The values of hyperparameter 1
    yticklabels -- The values of hyperparameter 2
    cmap -- The matplotlib color map
    vmin -- the minimum value
    vmax -- the maximum value
    ax -- The figure axes to plot on
    fmt -- formatting of the score values
    """
    if ax is None:
        ax = plt.gca()
    # plot the mean cross-validation scores
    img = ax.pcolor(values, cmap=cmap, vmin=None, vmax=None)
    img.update_scalarmappable()
    ax.set_xlabel(xlabel, fontsize=10)
    ax.set_ylabel(ylabel, fontsize=10)
    ax.set_xticks(np.arange(len(xticklabels)) + .5)
    ax.set_yticks(np.arange(len(yticklabels)) + .5)
    ax.set_xticklabels(xticklabels)
    ax.set_yticklabels(yticklabels)
    ax.set_aspect(1)
    
    ax.tick_params(axis='y', labelsize=12)
    ax.tick_params(axis='x', labelsize=12, labelrotation=90)

    for p, color, value in zip(img.get_paths(), img.get_facecolors(), img.get_array()):
        x, y = p.vertices[:-2, :].mean(0)
        if np.mean(color[:3]) > 0.5:
            c = 'k'
        else:
            c = 'w'
        ax.text(x, y, fmt % value, color=c, ha="center", va="center", size=10)
    return img

Exercise 1: Linear SVMs

First, we’ll look at linear SVMs and the different outputs they produce. Check the documentation of LinearSVC

The most important inputs are:

• C – The C hyperparameter controls the misclassification cost and therefore the amount of regularization. Lower values correspond to more regularization

• loss - The loss function, typically ‘hinge’ or ‘squared_hinge’. Squared hinge is the default. Normal hinge is less strict.

• dual – Whether to solve the primal optimization problem or the dual (default). The primal is recommended if you have many more data points than features (although our datasets is very small, so it won’t matter much).

The most important outputs are:

• decision_function - The function used to classify any point. In this case on linear SVMs, this corresponds to the learned hyperplane, or \(y = \mathbf{wX} + b\). It can be evaluated at every point, if the result is positive the point is classified as the positive class and vice versa.

• coef_ - The model coefficients, i.e. the weights \(\mathbf{w}\)

• intercept_ - the bias \(b\)

From the decision function we can find which points are support vectors and which are not: the support vectors are all the points that fall inside the margin, i.e. have a decision value between -1 and 1, or that are misclassified. Also see the lecture slides.

Exercise 1.1: Linear SVMs

Train a LinearSVC with C=0.001 and hinge loss. Then, use the plotting function plot_svm_kernel to plot the results. For this you need to extract the support vectors from the decision function. There is a hint below should you get stuck. Interpret the plot as detailed as you can. Afterwards you can also try some different settings. You can also try using the primal instead of the dual optimization problem (in that case, use squared hinge loss).

# Hint: how to compute the support vectors from the decision function (ignore if you want to solve this yourself)
# support_vector_indices = np.where((2 * y - 1) * clf.decision_function(X) <= 1)[0]
# support_vectors = X[support_vector_indices]

# Note that we can also calculate the decision function manually with the formula y = w*X
# decision_function = np.dot(X, clf.coef_[0]) + clf.intercept_[0]

Solution

plt.rcParams['figure.dpi'] = 200 # Make figures a bit bigger

from sklearn.svm import LinearSVC
clf1_1 = LinearSVC(C=0.001, loss='hinge')
clf1_1.fit(X, y)

support_vector_indices = np.where((2 * y - 1) * clf1_1.decision_function(X) <= 1)[0]
support_vectors = X[support_vector_indices]

plot_svm_kernel(X, y, "Linear SVM",support_vectors,clf1_1.decision_function)

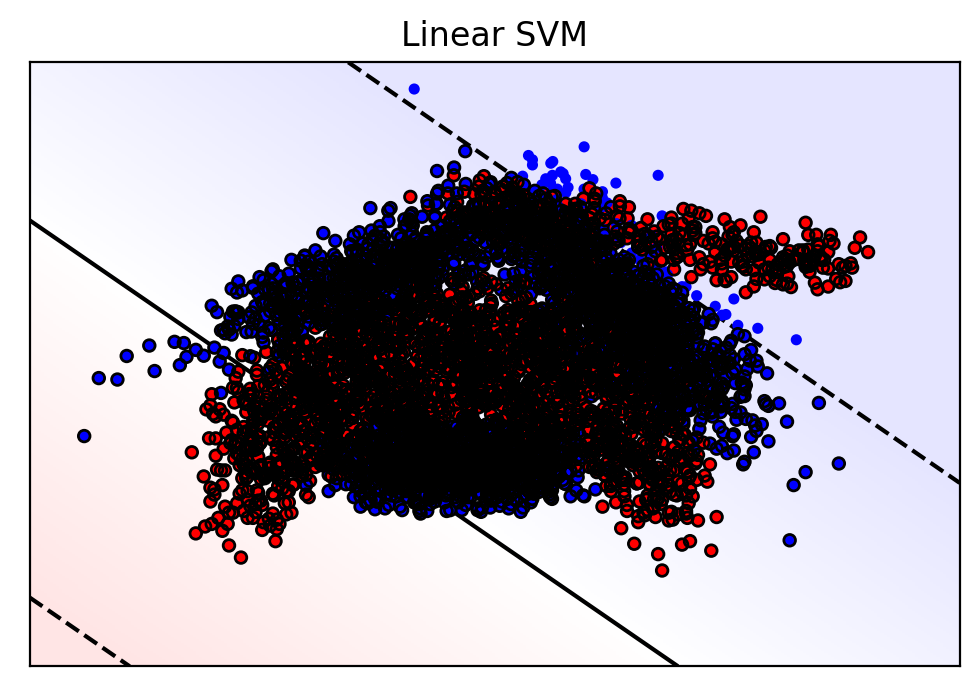
Interpretation: As expected, the data cannot be fitted well with a linear SVM. Almost all points fall within the margin. Almost all points are support vectors, except for a few blue points on the top right. The accuracy is only 57%.

Exercise 2: Kernelized SVMs

Check the documentation of SVC

It has a few more inputs. The most important:

• kernel - It must be either ‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, or your custom defined kernel.

• gamma - The kernel width of the rbf (Gaussian) kernel. Smaller values mean wider kernels. Only relevant when selecting the rbf kernel.

• degree - The degree of the polynomial kernel. Only relevant when selecting the poly kernel.

There also also more outputs that make our lifes easier:

• support_vectors_ - The array of support vectors

• n_support_ - The number of support vectors per class

• dual_coef_ - The coefficients of the support vectors (the dual coefficients)

Exercise 2.1

Evaluate different kernels, with their default hyperparameter settings. Outputs should be the 5-fold cross validated accuracy scores for the linear kernel (lin_scores), polynomial kernel (poly_scores) and RBF kernel (rbf_scores). Print the mean and variance of the scores and give an initial interpretation of the performance of each kernel.

Solution

#Imports
from sklearn import svm
from sklearn.model_selection import cross_val_score

# Linear kernel
clf = svm.SVC(kernel='linear')
lin_scores = cross_val_score(clf, X, y)

# Polynomial kernel
clf = svm.SVC(kernel='poly')
poly_scores = cross_val_score(clf, X, y)

# RBF kernel
clf = svm.SVC(kernel='rbf')
rbf_scores = cross_val_score(clf, X, y)

print("AUC Linear Kernel: {:.2f} +- {:.4f}".format(lin_scores.mean(), np.var(lin_scores)))
print("AUC Polynomial Kernel: {:.2f} +- {:.4f}".format(poly_scores.mean(), np.var(poly_scores)))
print("AUC RBF Kernel: {:.2f} +- {:.5f}".format(rbf_scores.mean(), np.var(rbf_scores)))

AUC Linear Kernel: 0.55 +- 0.0000
AUC Polynomial Kernel: 0.64 +- 0.0000
AUC RBF Kernel: 0.90 +- 0.00005

The linear kernel has a very low score, and is likely underfitting severely. The polynomial kernel does a lot better. The RBF kernel works particularly well, even without any tuning. The models are very stable, there is hardly any variance in the scores.

Exercise 2: Visualizing the fit

To better understand what the different kernels are doing, let’s visualize their predictions.

Exercise 2.1

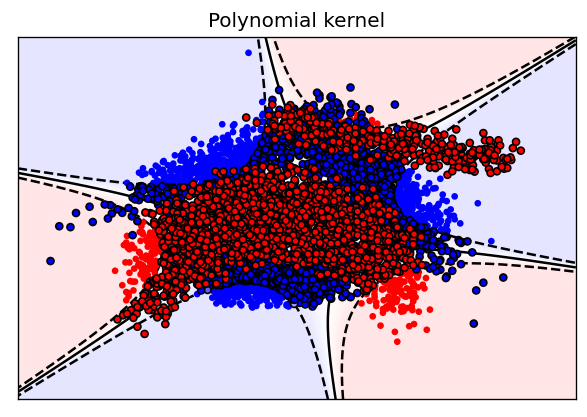
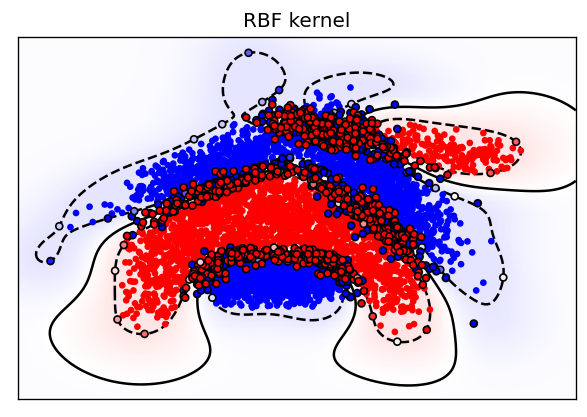
Call and fit SVM with linear, polynomial and RBF kernels with default parameter values. For RBF kernel, use kernel coefficient value (gamma) of 2.0. Plot the results for each kernel with “plot_svm_kernel” function. The plots show the predictions made for the different kernels. The background color shows the prediction (blue or red). The full line shows the decision boundary, and the dashed line the margin. The encircled points are the support vectors.

Solution

plt.rcParams['figure.dpi'] = 120 # Make figures a bit bigger

#Linear
clf1 = svm.SVC(kernel='linear', C=1.0, tol=1e-3)  #default values for parameters
clf1.fit(X, y)
plot_svm_kernel(X,y,"Linear kernel", 
                clf1.support_vectors_, 
                clf1.decision_function, clf1.dual_coef_)

#Polynomial
clf2 = svm.SVC(kernel='poly', C=1.0)
clf2.fit(X, y)
plot_svm_kernel(X,y,"Polynomial kernel", 
                clf2.support_vectors_, 
                clf2.decision_function, clf2.dual_coef_)

#RBF
clf3 = svm.SVC(kernel='rbf', gamma=2, C=1.0)
clf3.fit(X,y)
plot_svm_kernel(X,y,"RBF kernel", 
                clf3.support_vectors_, 
                clf3.decision_function, clf3.dual_coef_)

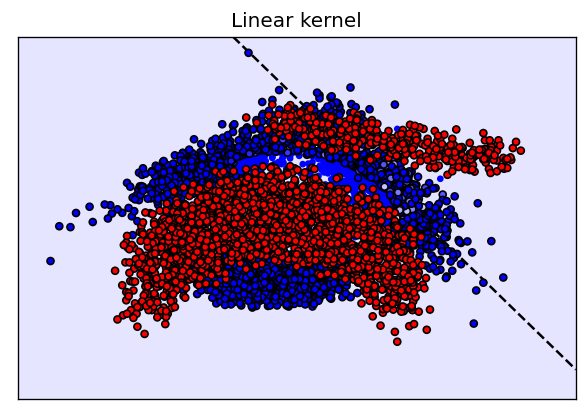
Exercise 2.2

Interpret the plots for each kernel. Think of ways to improve the results.

Solution

Linear: It’s clear that this data is not linearly separable. The linear SVM is badly underfitting. There also appear to be some optimization issues, as the decision boundary lies way outside of the image, and there is a group of non-support vectors that should be support vectors. Forcing more optimization (by decreasing tolerance of the stopping criterion tol) yields slightly better results, but will also slow down the optimization (try it of you like).

Polynomial: A slightly better fit, but clearly polynomials aren’t the best fit either. They divide the space in subspaces that don’t capture the banana shapes at all.

RBF: Works very nicely, and the default settings seem to actually hit the sweet spot. We should still try to tune C and gamma.

Exercise 3: Visualizing the RBF models and hyperparameter space

Select the RBF kernel and optimize the two most important hyperparameters (the 𝐶 parameter and the kernel width 𝛾 ).

Hint: values for C and \(\gamma\) are typically in [\(2^{-15}..2^{15}\)] on a log scale.

Exercise 3.1

First try 3 very different values for \(C\) and \(\gamma\) (for instance [1e-3,1,1e3]). For each of the 9 combinations, create the same RBF plot as before to understand what the model is doing. Also create a standard train-test split and report the train and test score. Explain the performance results. When are you over/underfitting? Can you see this in the predictions?

Solution

from sklearn.model_selection import train_test_split

# For convenience we'll plot the results in a 3x3 grid
plt.figure(figsize=(15, 10))
fig_num = 0

# build a standard stratified train-test split
X_train, X_test, y_train, y_test = train_test_split(X,y, stratify=y, random_state=0)

for c in [0.001, 1, 1000]:
    for gamma in [0.001, 1, 1000]:
        fig_num += 1
        plt.subplot(3, 3, fig_num) # plot in a 3x3 grid
        clf4 = svm.SVC(kernel='rbf',C=float(c),gamma=float(gamma)) # setup and fit the model
        clf4.fit(X_train, y_train)
        plot_svm_kernel(X_train,y_train,"C={}, g={}, trainACC {:.2f}, testACC {:.2f}".format(c,gamma,clf4.score(X_train,y_train), clf4.score(X_test,y_test)), 
                clf4.support_vectors_, clf4.decision_function, clf4.dual_coef_, show=False)
        
plt.show();

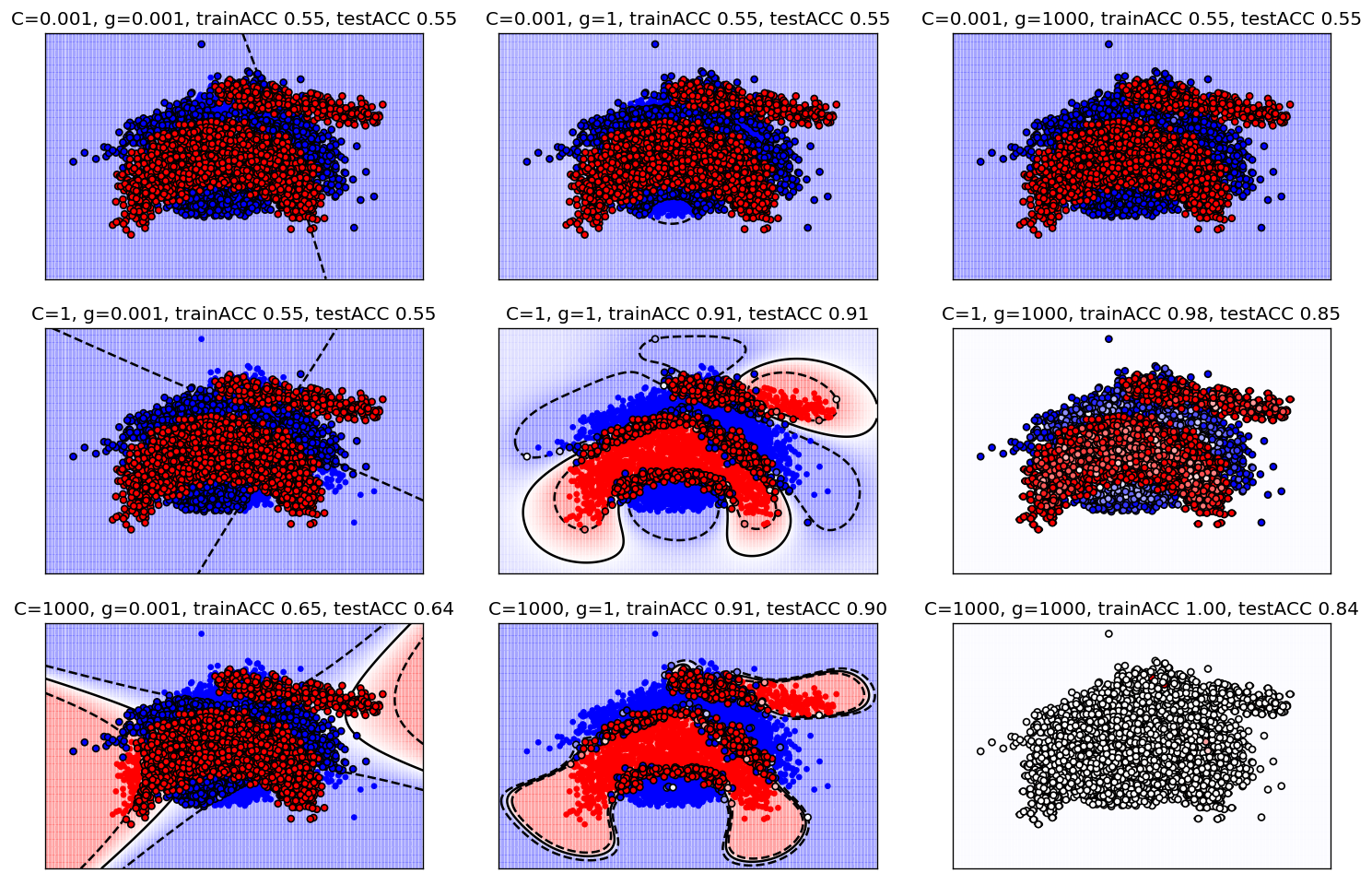
• For C = 0.001 (top row), the SVM is always underfitting. The boundaries look very different but all are underfitting because they are over-regularized.

• For gamma = 1000 (narrow Gaussians, right column), almost all datapoints are support vectors, For higher values of C, they are clearly overfitting: the decision boundaries are islands around each point, the model predicts 0 everywhere else.

• The best results are found for medium C, medium gamma. This also yields the fewest support vectors. The decision boundaries show that it captures the banana shapes well.

• Large C values (bottom row) tend to cause more overfitting unless gamma is very small. These two types of regularization clearly interact with each other.

• For gamma=1, you can also see that the margins for C=1000 are much more narrow than those for C=1. Although not visible in the scores, it is clear that the center model (with the larger margins) will generalize better.

Exercise 3.2

Optimize the hyperparameters using a grid search, trying every possible combination of C and gamma. Show a heatmap of the results and report the optimal hyperparameter values. Use at least 10 values for \(C\) and \(\gamma\) in [\(2^{-15}..2^{15}\)] on a log scale. Report accuracy under 3-fold CV. We recommend to use sklearn’s GridSearchCV and the heatmap function defined above. Check their documentation.

Solution

from sklearn.model_selection import GridSearchCV

# Define and fit a grid search with 3-fold cross validation for SVM - RBF kernel. 
# Quite a detailed grid search. May take a while.
svc = svm.SVC(kernel='rbf')
resolution = 25
param_grid = {'C': np.logspace(-12,12,resolution,base=2),
              'gamma': np.logspace(-12,12,resolution,base=2)}
grid_search = GridSearchCV(svc, param_grid, cv=3, n_jobs=-1, scoring='accuracy');
grid_search.fit(X, y);

#Plot with heatmap
results = pd.DataFrame(grid_search.cv_results_)
scores = np.array(results.mean_test_score).reshape(resolution, resolution)
plt.rcParams.update({'font.size': 18})
fig, axes = plt.subplots(1, 1, figsize=(13, 13))
heatmap(scores, xlabel='gamma', xticklabels=np.around(param_grid['gamma'],4),
                      ylabel='C', yticklabels=np.around(param_grid['C'],4), cmap="viridis", fmt="%.2f", ax=axes);

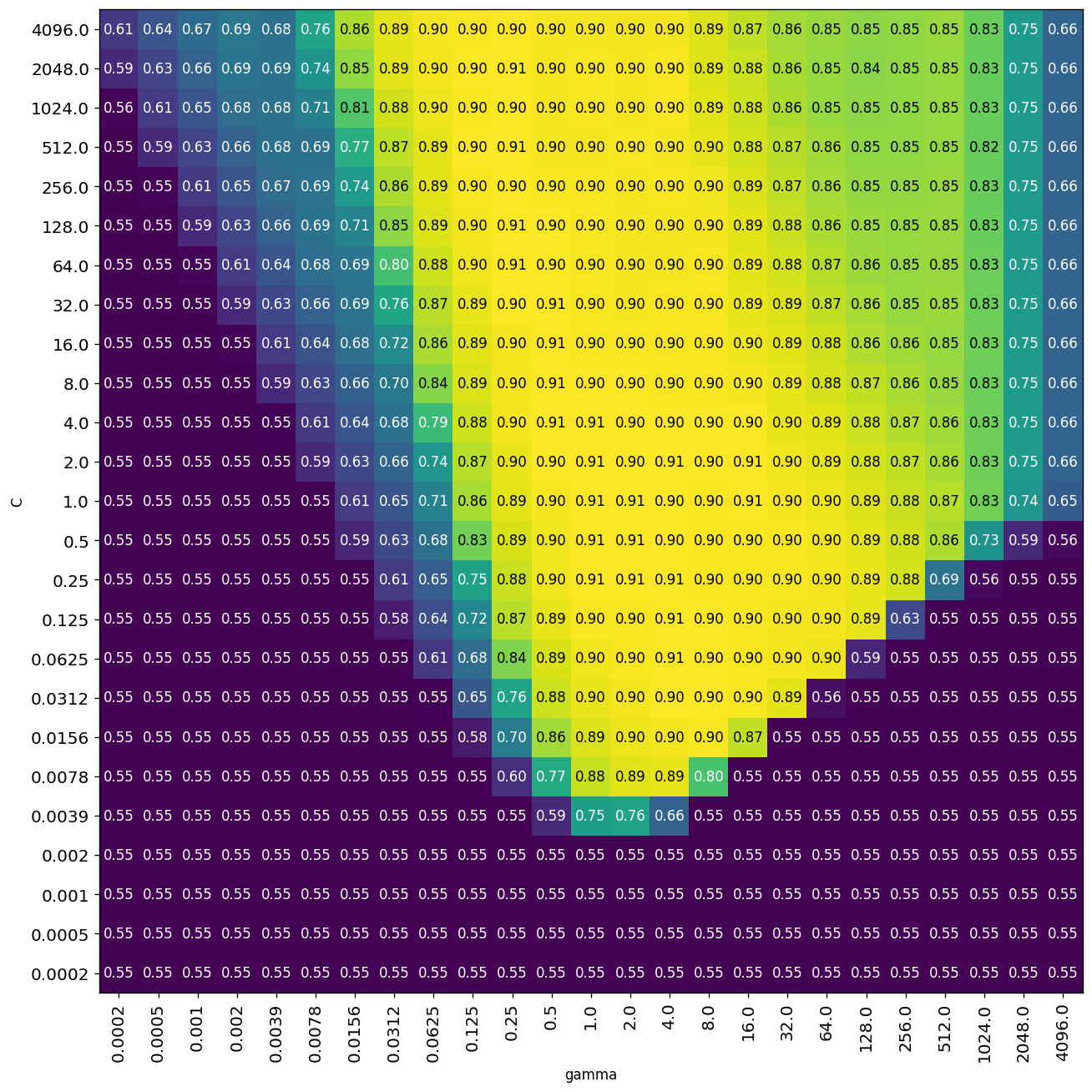
We can see that there isn’t really an simple optimal peak in the C-gamma space, but rather a ‘ridge’ of optimal performance. For instance, (gamma=0.25, C=4096) has top performance, but so does (gamma=2.0, C=0.25).