Lecture 8. Neural Networks

Lecture 8. Neural Networks#

How to train your neurons

Joaquin Vanschoren

Overview#

Neural architectures
Training neural nets
- Forward pass: Tensor operations
- Backward pass: Backpropagation
Neural network design:
- Activation functions
- Weight initialization
- Optimizers
Neural networks in practice
Model selection
- Early stopping
- Memorization capacity and information bottleneck
- L1/L2 regularization
- Dropout
- Batch normalization

Architecture#

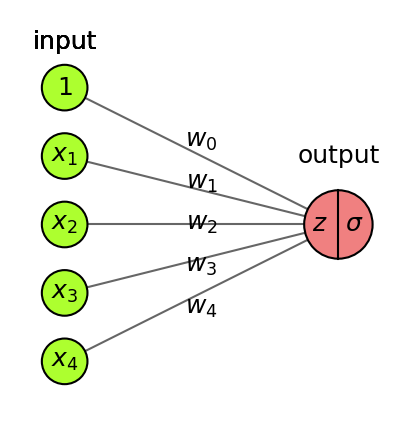
Logistic regression, drawn in a different, neuro-inspired, way
- Linear model: inner product ($z$) of input vector $\mathbf{x}$ and weight vector $\mathbf{w}$, plus bias $w_0$
- Logistic (or sigmoid) function maps the output to a probability in [0,1]
- Uses log loss (cross-entropy) and gradient descent to learn the weights

\[\hat{y}(\mathbf{x}) = \text{sigmoid}(z) = \text{sigmoid}(w_0 + \mathbf{w}\mathbf{x}) = \text{sigmoid}(w_0 + w_1 * x_1 + w_2 * x_2 +... + w_p * x_p)\]

../_images/a2278a179abd1ac3e43803acea26e35120ab1c85bb6592dd1fab8c979099427d.png

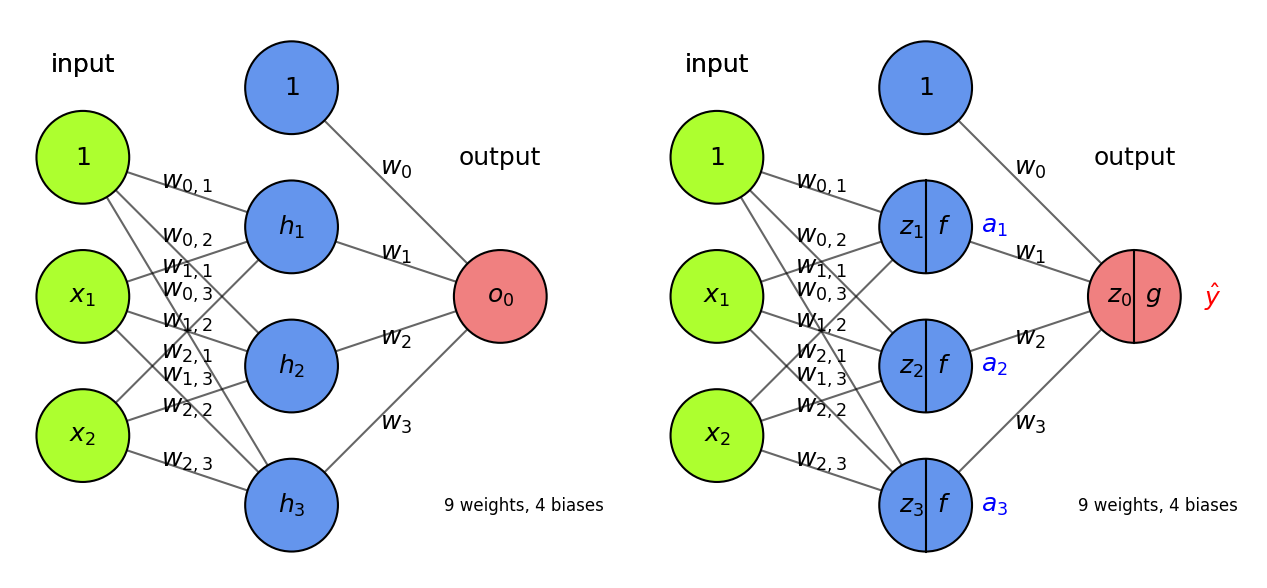
Basic Architecture#

Add one (or more) hidden layers $h$ with $k$ nodes (or units, cells, neurons)
- Every ‘neuron’ is a tiny function, the network is an arbitrarily complex function
- Weights $w_{i,j}$ between node $i$ and node $j$ form a weight matrix $\mathbf{W}^{(l)}$ per layer $l$
Every neuron weights the inputs $\mathbf{x}$ and passes it through a non-linear activation function
- Activation functions ($f,g$) can be different per layer, output $\mathbf{a}$ is called activation $$\color{blue}{h(\mathbf{x})} = \color{blue}{\mathbf{a}} = f(\mathbf{z}) = f(\mathbf{W}^{(1)} \color{green}{\mathbf{x}}+\mathbf{w}^{(1)}_0) \quad \quad \color{red}{o(\mathbf{x})} = g(\mathbf{W}^{(2)} \color{blue}{\mathbf{a}}+\mathbf{w}^{(2)}_0)$$

../_images/f93a3001a9718adebe751babf6e9756747c486a96d60d9ed50919075f6318e8f.png

More layers#

Add more layers, and more nodes per layer, to make the model more complex
- For simplicity, we don’t draw the biases (but remember that they are there)
In dense (fully-connected) layers, every previous layer node is connected to all nodes
The output layer can also have multiple nodes (e.g. 1 per class in multi-class classification)

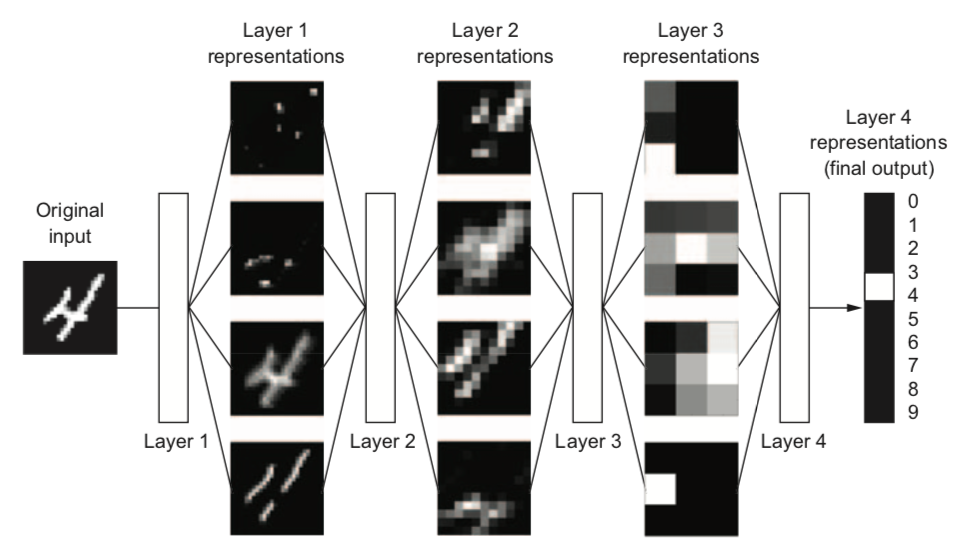
Why layers?#

Each layer acts as a filter and learns a new representation of the data
- Subsequent layers can learn iterative refinements
- Easier that learning a complex relationship in one go
Example: for image input, each layer yields new (filtered) images
- Can learn multiple mappings at once: weight tensor $\mathit{W}$ yields activation tensor $\mathit{A}$
- From low-level patterns (edges, end-points, …) to combinations thereof
- Each neuron ‘lights up’ if certain patterns occur in the input

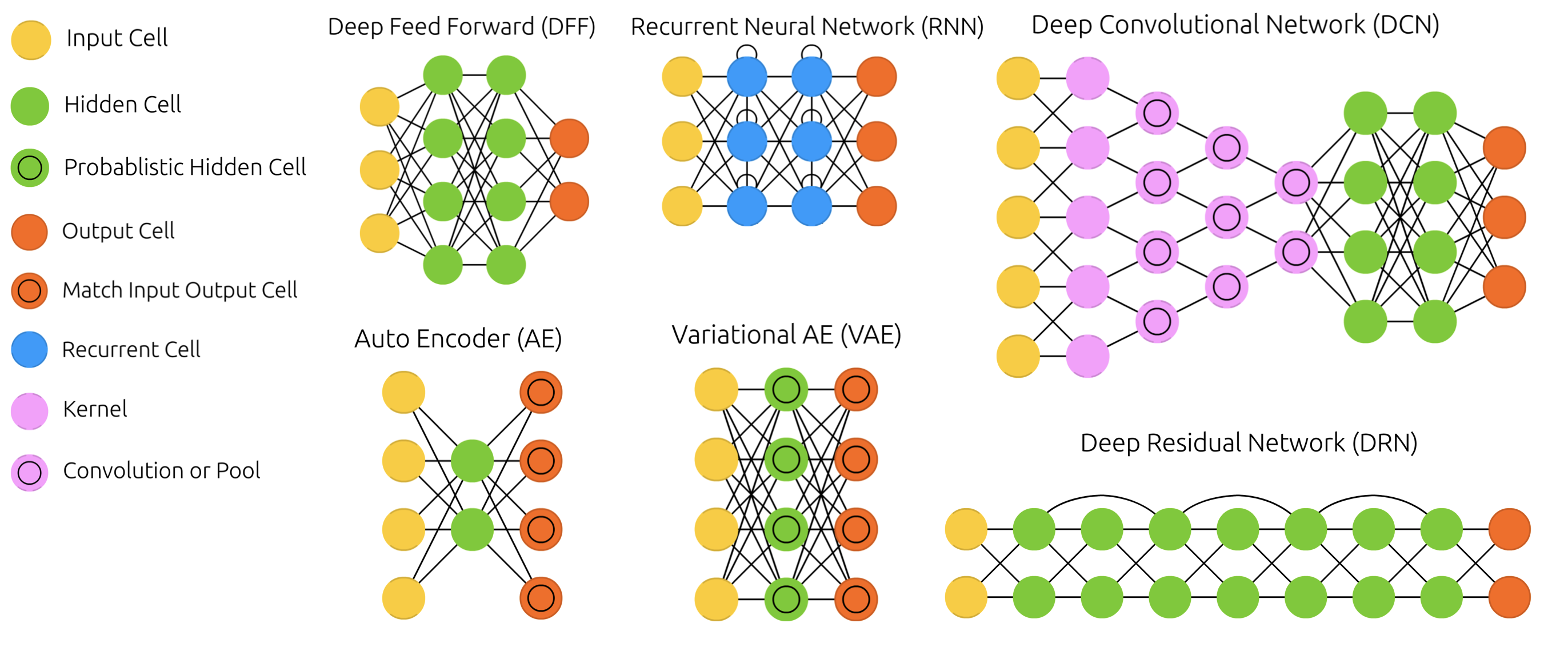
Other architectures#

There exist MANY types of networks for many different tasks
Convolutional nets for image data, Recurrent nets for sequential data,…
Also used to learn representations (embeddings), generate new images, text,…

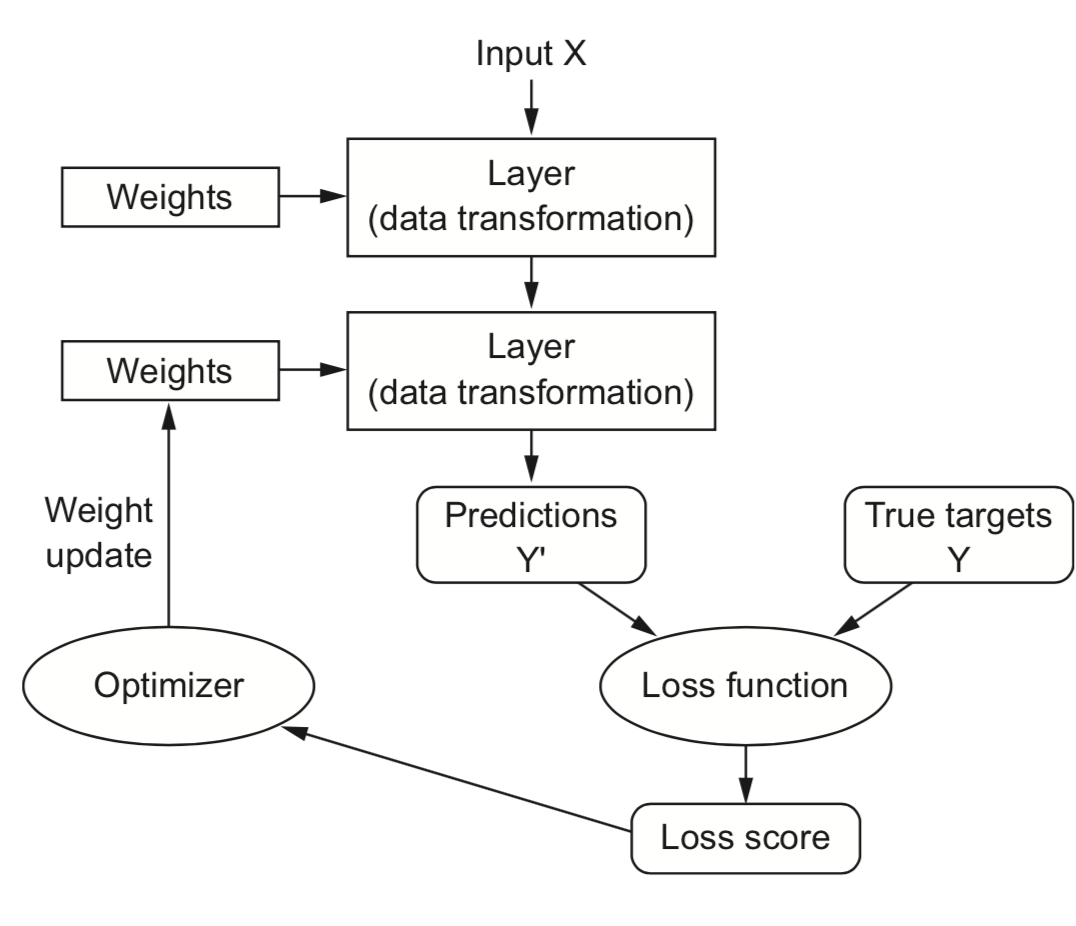
Training Neural Nets#

Design the architecture, choose activation functions (e.g. sigmoids)
Choose a way to initialize the weights (e.g. random initialization)
Choose a loss function (e.g. log loss) to measure how well the model fits training data
Choose an optimizer (typically an SGD variant) to update the weights

Mini-batch Stochastic Gradient Descent (recap)#

Draw a batch of batch_size training data $\mathbf{X}$ and $\mathbf{y}$
Forward pass : pass $\mathbf{X}$ though the network to yield predictions $\mathbf{\hat{y}}$
Compute the loss $\mathcal{L}$ (mismatch between $\mathbf{\hat{y}}$ and $\mathbf{y}$)
Backward pass : Compute the gradient of the loss with regard to every weight
- Backpropagate the gradients through all the layers
Update $W$: $W_{(i+1)} = W_{(i)} - \frac{\partial L(x, W_{(i)})}{\partial W} * \eta$

Repeat until n passes (epochs) are made through the entire training set

Forward pass#

We can naturally represent the data as tensors
- Numerical n-dimensional array (with n axes)
- 2D tensor: matrix (samples, features)
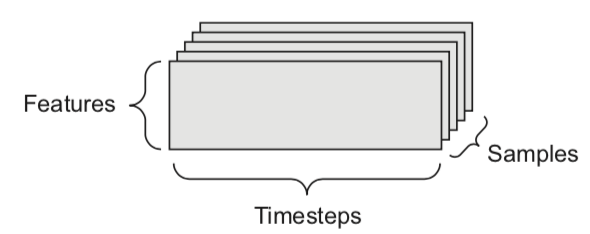
- 3D tensor: time series (samples, timesteps, features)
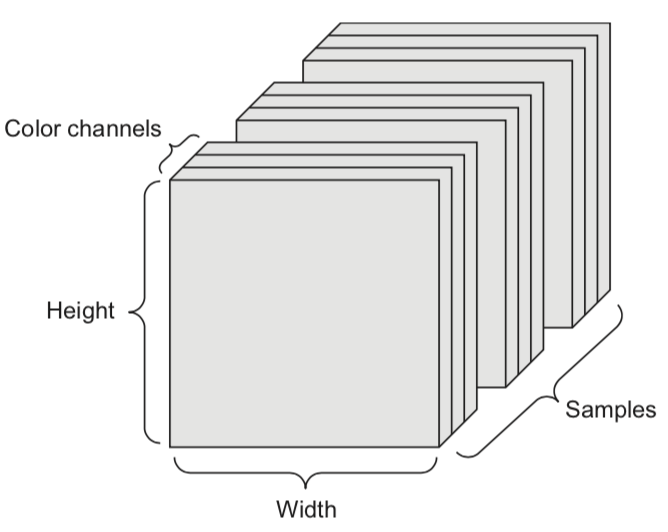
- 4D tensor: color images (samples, height, width, channels)
- 5D tensor: video (samples, frames, height, width, channels)

Tensor operations#

The operations that the network performs on the data can be reduced to a series of tensor operations
- These are also much easier to run on GPUs
A dense layer with sigmoid activation, input tensor $\mathbf{X}$, weight tensor $\mathbf{W}$, bias $\mathbf{b}$:

y = sigmoid(np.dot(X, W) + b)

Tensor dot product for 2D inputs ($a$ samples, $b$ features, $c$ hidden nodes)

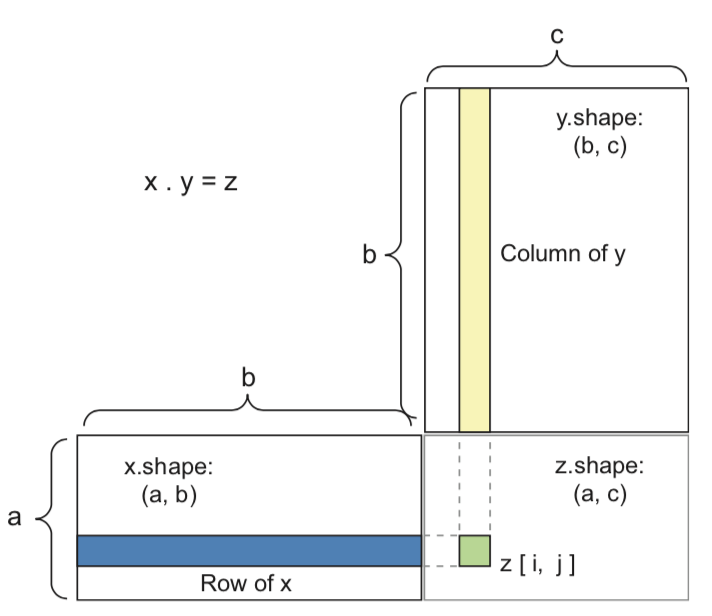
Element-wise operations#

Activation functions and addition are element-wise operations:

def sigmoid(x):
  return 1/(1 + np.exp(-x)) 

def add(x, y):
  return x + y

Note: if y has a lower dimension than x, it will be broadcasted: axes are added to match the dimensionality, and y is repeated along the new axes

>>> np.array([[1,2],[3,4]]) + np.array([10,20])
array([[11, 22],
       [13, 24]])

Backward pass (backpropagation)#

For last layer, compute gradient of the loss function $\mathcal{L}$ w.r.t all weights of layer $l$

\[\begin{split}\nabla \mathcal{L} = \frac{\partial \mathcal{L}}{\partial W^{(l)}} = \begin{bmatrix} \frac{\partial \mathcal{L}}{\partial w_{0,0}} & \ldots & \frac{\partial \mathcal{L}}{\partial w_{0,l}} \\ \vdots & \ddots & \vdots \\ \frac{\partial \mathcal{L}}{\partial w_{k,0}} & \ldots & \frac{\partial \mathcal{L}}{\partial w_{k,l}} \end{bmatrix}\end{split}\]

Sum up the gradients for all $\mathbf{x}_j$ in minibatch: $\sum_{j} \frac{\partial \mathcal{L}(\mathbf{x}_j,y_j)}{\partial W^{(l)}}$
Update all weights in a layer at once (with learning rate $\eta$): $W_{(i+1)}^{(l)} = W_{(i)}^{(l)} - \eta \sum_{j} \frac{\partial \mathcal{L}(\mathbf{x}_j,y_j)}{\partial W_{(i)}^{(l)}}$
Repeat for next layer, iterating backwards (most efficient, avoids redundant calculations)

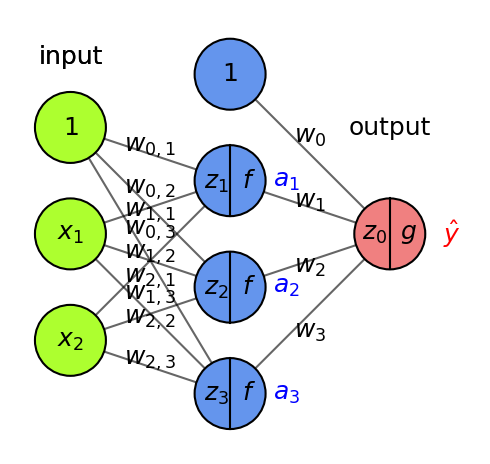
Example#

Imagine feeding a single data point, output is $\hat{y} = g(z) = g(w_0 + w_1 * a_1 + w_2 * a_2 +... + w_p * a_p)$
Decrease loss by updating weights:
- Update the weights of last layer to maximize improvement: $w_{i,(new)} = w_{i} - \frac{\partial \mathcal{L}}{\partial w_i} * \eta$
- To compute gradient $\frac{\partial \mathcal{L}}{\partial w_i}$ we need the chain rule: $f(g(x)) = f'(g(x)) * g'(x)$ $$\frac{\partial \mathcal{L}}{\partial w_i} = \color{red}{\frac{\partial \mathcal{L}}{\partial g}} \color{blue}{\frac{\partial \mathcal{g}}{\partial z_0}} \color{green}{\frac{\partial \mathcal{z_0}}{\partial w_i}}$$
E.g., with $\mathcal{L} = \frac{1}{2}(y-\hat{y})^2$ and sigmoid $\sigma$: $\frac{\partial \mathcal{L}}{\partial w_i} = \color{red}{(y - \hat{y})} * \color{blue}{\sigma'(z_0)} * \color{green}{a_i}$

../_images/65598d257efce5151b7c6d48db2a00ec4557b536c69bb2472a87540d5022b949.png

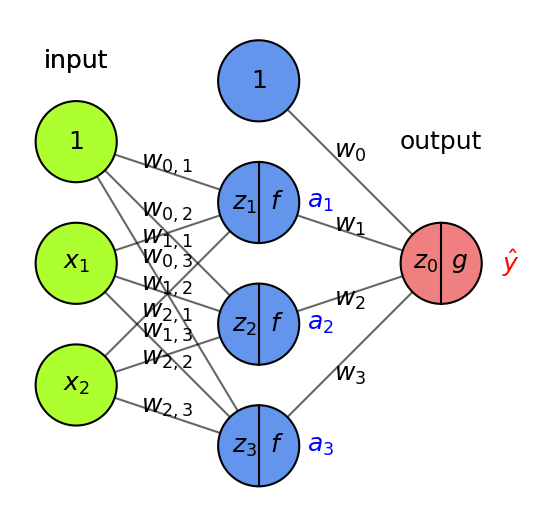
Backpropagation (2)#

Another way to decrease the loss $\mathcal{L}$ is to update the activations $a_i$
- To update $a_i = f(z_i)$, we need to update the weights of the previous layer
- We want to nudge $a_i$ in the right direction by updating $w_{i,j}$: $$\frac{\partial \mathcal{L}}{\partial w_{i,j}} = \frac{\partial \mathcal{L}}{\partial a_i} \frac{\partial a_i}{\partial z_i} \frac{\partial \mathcal{z_i}}{\partial w_{i,j}} = \left( \frac{\partial \mathcal{L}}{\partial g} \frac{\partial \mathcal{g}}{\partial z_0} \frac{\partial \mathcal{z_0}}{\partial a_i} \right) \frac{\partial a_i}{\partial z_i} \frac{\partial \mathcal{z_i}}{\partial w_{i,j}}$$
- We know $\frac{\partial \mathcal{L}}{\partial g}$ and $\frac{\partial \mathcal{g}}{\partial z_0}$ from the previous step, $\frac{\partial \mathcal{z_0}}{\partial a_i} = w_i$, $\frac{\partial a_i}{\partial z_i} = f'$ and $\frac{\partial \mathcal{z_i}}{\partial w_{i,j}} = x_j$

../_images/f4e22b491ee99795a0c5802ec99c3640336fd249557088a3927cf65b6d280241.png

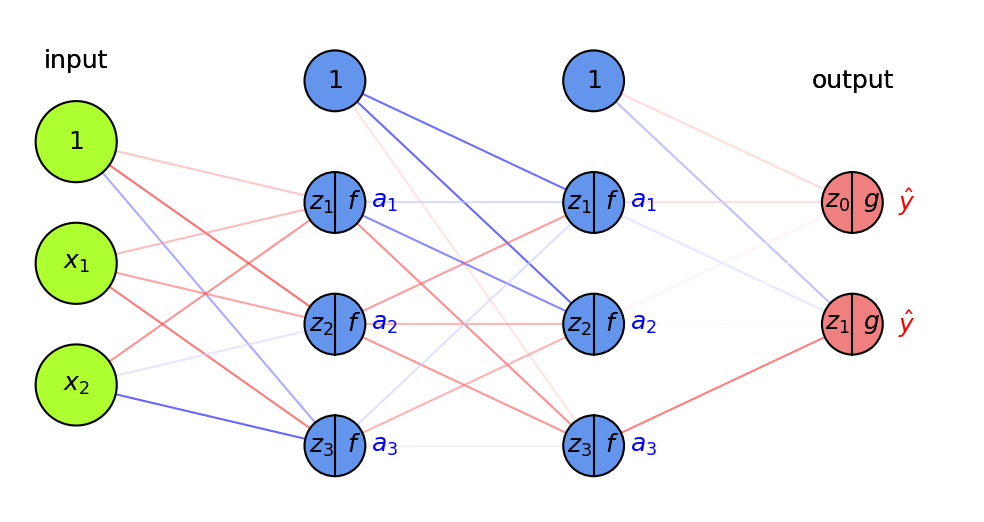
Backpropagation (3)#

With multiple output nodes, $\mathcal{L}$ is the sum of all per-output (per-class) losses
- $\frac{\partial \mathcal{L}}{\partial a_i}$ is sum of the gradients for every output
Per layer, sum up gradients for every point $\mathbf{x}$ in the batch: $\sum_{j} \frac{\partial \mathcal{L}(\mathbf{x}_j,y_j)}{\partial W}$
Update all weights of every layer $l$
- $W_{(i+1)}^{(l)} = W_{(i)}^{(l)} - \eta \sum_{j} \frac{\partial \mathcal{L}(\mathbf{x}_j,y_j)}{\partial W_{(i)}^{(l)}}$
Repeat with a new batch of data until loss converges
Nice animation of the entire process

../_images/3bada53e8069df4dced0e85f623d2ee2cdacb6053aab2cc2d7fc782083596722.png

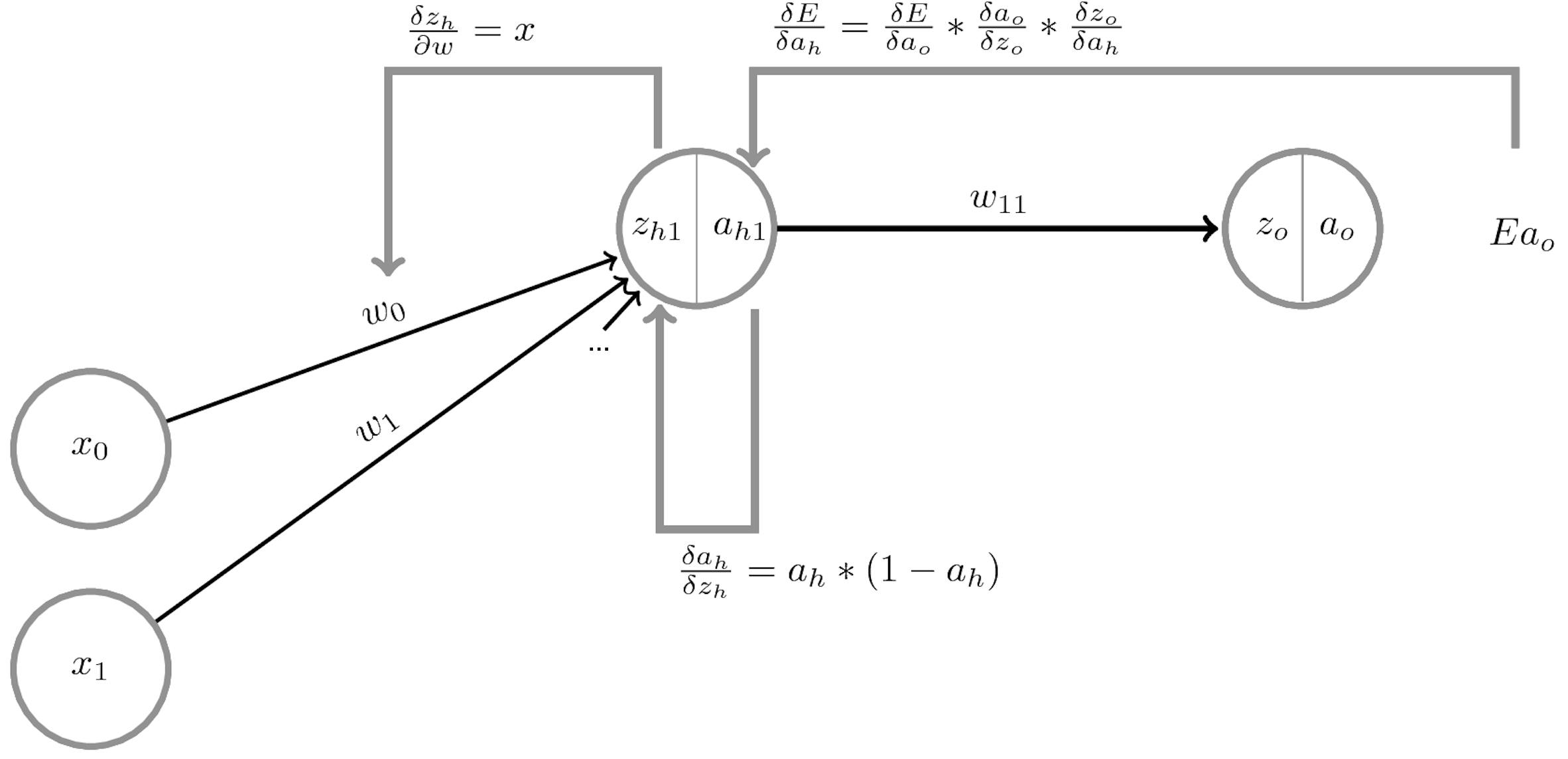
Summary#

The network output $a_o$ is defined by the weights $W^{(o)}$ and biases $\mathbf{b}^{(o)}$ of the output layer, and
The activations of a hidden layer $h_1$ with activation function $a_{h_1}$, weights $W^{(1)}$ and biases $\mathbf{b^{(1)}}$:

\[\color{red}{a_o(\mathbf{x})} = \color{red}{a_o(\mathbf{z_0})} = \color{red}{a_o(W^{(o)}} \color{blue}{a_{h_1}(z_{h_1})} \color{red}{+ \mathbf{b}^{(o)})} = \color{red}{a_o(W^{(o)}} \color{blue}{a_{h_1}(W^{(1)} \color{green}{\mathbf{x}} + \mathbf{b}^{(1)})} \color{red}{+ \mathbf{b}^{(o)})} \]

Minimize the loss by SGD. For layer $l$, compute $\frac{\partial \mathcal{L}(a_o(x))}{\partial W_l}$ and $\frac{\partial \mathcal{L}(a_o(x))}{\partial b_{l,i}}$ using the chain rule
Decomposes into gradient of layer above, gradient of activation function, gradient of layer input:

\[\frac{\partial \mathcal{L}(a_o)}{\partial W^{(1)}} = \color{red}{\frac{\partial \mathcal{L}(a_o)}{\partial a_{h_1}}} \color{blue}{\frac{\partial a_{h_1}}{\partial z_{h_1}}} \color{green}{\frac{\partial z_{h_1}}{\partial W^{(1)}}} = \left( \color{red}{\frac{\partial \mathcal{L}(a_o)}{\partial a_o}} \color{blue}{\frac{\partial a_o}{\partial z_o}} \color{green}{\frac{\partial z_o}{\partial a_{h_1}}}\right) \color{blue}{\frac{\partial a_{h_1}}{\partial z_{h_1}}} \color{green}{\frac{\partial z_{h_1}}{\partial W^{(1)}}} \]

Activation functions for hidden layers#

Sigmoid: $f(z) = \frac{1}{1+e^{-z}}$
Tanh: $f(z) = \frac{2}{1+e^{-2z}} - 1$
- Activations around 0 are better for gradient descent convergence
Rectified Linear (ReLU): $f(z) = max(0,z)$
- Less smooth, but much faster (note: not differentiable at 0)
Leaky ReLU: $f(z) = \begin{cases} 0.01z & z<0 \\ z & otherwise \end{cases}$

Effect of activation functions on the gradient#

During gradient descent, the gradient depends on the activation function $a_{h}$: $\frac{\partial \mathcal{L}(a_o)}{\partial W^{(l)}} = \color{red}{\frac{\partial \mathcal{L}(a_o)}{\partial a_{h_l}}} \color{blue}{\frac{\partial a_{h_l}}{\partial z_{h_l}}} \color{green}{\frac{\partial z_{h_l}}{\partial W^{(l)}}}$
If derivative of the activation function $\color{blue}{\frac{\partial a_{h_l}}{\partial z_{h_l}}}$ is 0, the weights $w_i$ are not updated
- Moreover, the gradients of previous layers will be reduced (vanishing gradient)
sigmoid, tanh: gradient is very small for large inputs: slow updates
With ReLU, $\color{blue}{\frac{\partial a_{h_l}}{\partial z_{h_l}}} = 1$ if $z>0$, hence better against vanishing gradients
- Problem: for very negative inputs, the gradient is 0 and may never recover (dying ReLU)
- Leaky ReLU has a small (0.01) gradient there to allow recovery

ReLU vs Tanh#

What is the effect of using non-smooth activation functions?
- ReLU produces piecewise-linear boundaries, but allows deeper networks
- Tanh produces smoother decision boundaries, but is slower

Activation functions for output layer#

sigmoid converts output to probability in [0,1]
- For binary classification
softmax converts all outputs (aka ‘logits’) to probabilities that sum up to 1
- For multi-class classification ($k$ classes)
- Can cause over-confident models. If so, smooth the labels: $y_{smooth} = (1-\alpha)y + \frac{\alpha}{k}$ $$\text{softmax}(\mathbf{x},i) = \frac{e^{x_i}}{\sum_{j=1}^k e^{x_j}}$$
For regression, don’t use any activation function, let the model learn the exact target

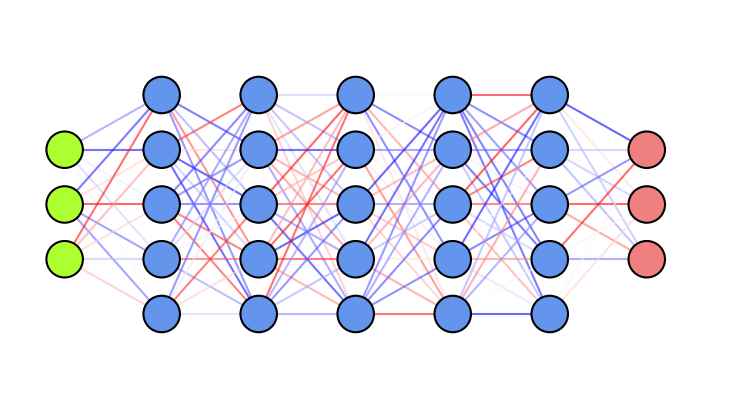
Weight initialization#

Initializing weights to 0 is bad: all gradients in layer will be identical (symmetry)
Too small random weights shrink activations to 0 along the layers (vanishing gradient)
Too large random weights multiply along layers (exploding gradient, zig-zagging)
Ideal: small random weights + variance of input and output gradients remains the same
- Glorot/Xavier initialization (for tanh): randomly sample from $N(0,\sigma), \sigma = \sqrt{\frac{2}{\text{fan_in + fan_out}}}$
  - fan_in: number of input units, fan_out: number of output units
- He initialization (for ReLU): randomly sample from $N(0,\sigma), \sigma = \sqrt{\frac{2}{\text{fan_in}}}$
- Uniform sampling (instead of $N(0,\sigma)$) for deeper networks (w.r.t. vanishing gradients)

../_images/29cf0f5ca7cae28623384cc0aa544eb6f7ee1fc66facc2c2832bf4efb7500225.png

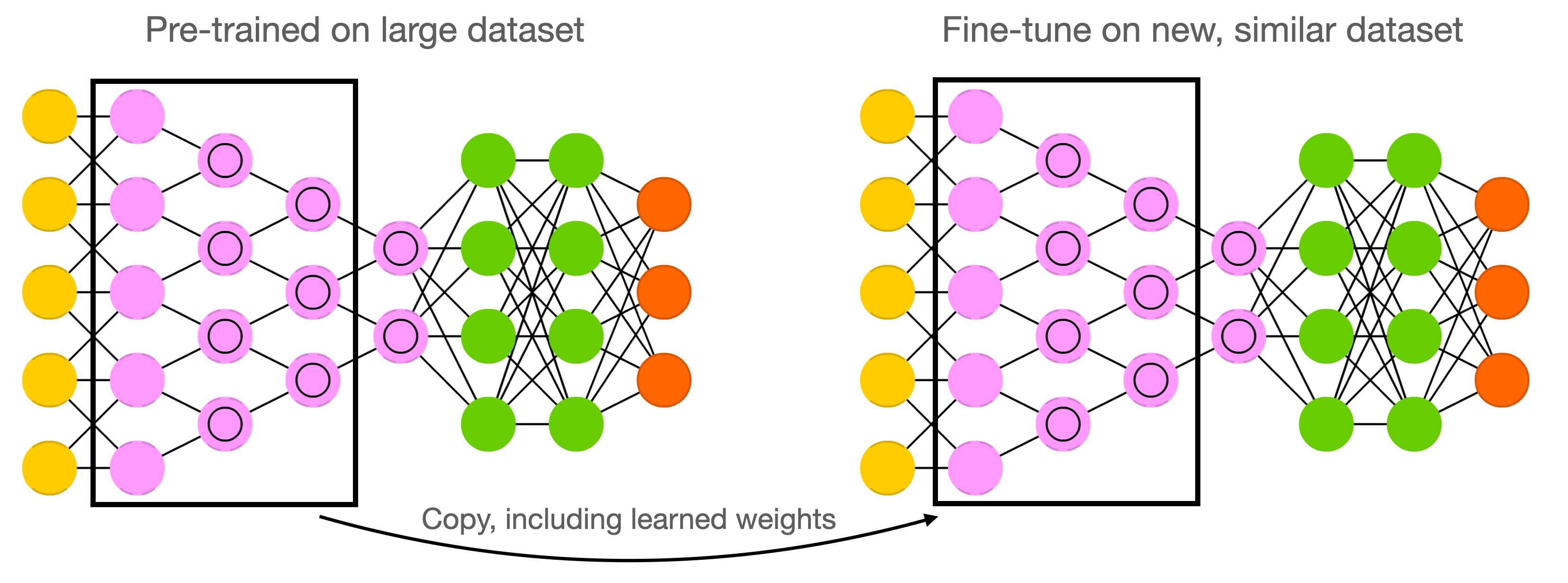
Weight initialization: transfer learning#

Instead of starting from scratch, start from weights previously learned from similar tasks
- This is, to a big extent, how humans learn so fast
Transfer learning: learn weights on task T, transfer them to new network
- Weights can be frozen, or finetuned to the new data
Only works if the previous task is ‘similar’ enough
- Generally, weights learned on very diverse data (e.g. ImageNet) transfer better
- Meta-learning: learn a good initialization across many related tasks

import tensorflow as tf
import tensorflow_addons as tfa

# Toy surface
def f(x, y):
    return (1.5 - x + x*y)**2 + (2.25 - x + x*y**2)**2 + (2.625 - x + x*y**3)**2

# Tensorflow optimizers
sgd = tf.optimizers.SGD(0.01)
lr_schedule = tf.optimizers.schedules.ExponentialDecay(0.02,decay_steps=100,decay_rate=0.96)
sgd_decay = tf.optimizers.SGD(learning_rate=lr_schedule)
#sgd_cyclic = tfa.optimizers.CyclicalLearningRate(initial_learning_rate= 0.1, maximal_learning_rate= 0.5, step_size=0.05)
clr_schedule = tfa.optimizers.CyclicalLearningRate(initial_learning_rate=1e-4, maximal_learning_rate= 0.1, 
                                                   step_size=100, scale_fn=lambda x : x)
sgd_cyclic = tf.optimizers.SGD(learning_rate=clr_schedule)
momentum = tf.optimizers.SGD(0.005, momentum=0.9, nesterov=False)
nesterov = tf.optimizers.SGD(0.005, momentum=0.9, nesterov=True)
adagrad = tf.optimizers.Adagrad(0.4)
#adamax = tf.optimizers.Adamax(learning_rate=0.5, beta_1=0.9, beta_2=0.999) # AdaMax is still not supported in tensorflow-metal
#adadelta = tf.optimizers.Adadelta(learning_rate=1.0)
rmsprop = tf.optimizers.RMSprop(learning_rate=0.1)
#rmsprop_momentum = tf.optimizers.RMSprop(learning_rate=0.1, momentum=0.9)
adam = tf.optimizers.Adam(learning_rate=0.2, beta_1=0.9, beta_2=0.999, epsilon=1e-8)

optimizers = [sgd, sgd_decay, momentum, nesterov, adagrad, rmsprop, adam, sgd_cyclic] #, adamax]
opt_names = ['sgd', 'sgd_decay', 'momentum', 'nesterov', 'adagrad', 'rmsprop', 'adam', 'sgd_cyclic'] #,'adamax']
cmap = plt.cm.get_cmap('tab10')
colors = [cmap(x/10) for x in range(10)]

# Training
all_paths = []
for opt, name in zip(optimizers, opt_names):
    x = tf.Variable(0.8)
    y = tf.Variable(1.6)

    x_history = []
    y_history = []
    loss_prev = 0.0
    max_steps = 100
    for step in range(max_steps):
        with tf.GradientTape() as g:
            loss = f(x, y)
            x_history.append(x.numpy())
            y_history.append(y.numpy())
            grads = g.gradient(loss, [x, y])
            opt.apply_gradients(zip(grads, [x, y]))

    if np.abs(loss_prev - loss.numpy()) < 1e-6:
        break
    loss_prev = loss.numpy()
    x_history = np.array(x_history)
    y_history = np.array(y_history)
    path = np.concatenate((np.expand_dims(x_history, 1), np.expand_dims(y_history, 1)), axis=1).T
    all_paths.append(path)

WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
2024-03-17 20:49:38.127852: I metal_plugin/src/device/metal_device.cc:1154] Metal device set to: Apple M1 Pro
2024-03-17 20:49:38.127875: I metal_plugin/src/device/metal_device.cc:296] systemMemory: 16.00 GB
2024-03-17 20:49:38.127880: I metal_plugin/src/device/metal_device.cc:313] maxCacheSize: 5.33 GB
2024-03-17 20:49:38.127930: I tensorflow/core/common_runtime/pluggable_device/pluggable_device_factory.cc:306] Could not identify NUMA node of platform GPU ID 0, defaulting to 0. Your kernel may not have been built with NUMA support.
2024-03-17 20:49:38.127968: I tensorflow/core/common_runtime/pluggable_device/pluggable_device_factory.cc:272] Created TensorFlow device (/job:localhost/replica:0/task:0/device:GPU:0 with 0 MB memory) -> physical PluggableDevice (device: 0, name: METAL, pci bus id: <undefined>)
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.Adagrad` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.Adagrad`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.RMSprop` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.RMSprop`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.Adam` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.Adam`.

# Plotting
number_of_points = 50
margin = 4.5
minima = np.array([3., .5])
minima_ = minima.reshape(-1, 1)
x_min = 0. - 2
x_max = 0. + 3.5
y_min = 0. - 3.5
y_max = 0. + 2
x_points = np.linspace(x_min, x_max, number_of_points) 
y_points = np.linspace(y_min, y_max, number_of_points)
x_mesh, y_mesh = np.meshgrid(x_points, y_points)
z = np.array([f(xps, yps) for xps, yps in zip(x_mesh, y_mesh)])

def plot_optimizers(ax, iterations, optimizers):
    ax.contour(x_mesh, y_mesh, z, levels=np.logspace(-0.5, 5, 25), norm=LogNorm(), cmap=plt.cm.jet, linewidths=fig_scale, zorder=-1)
    ax.plot(*minima, 'r*', markersize=20*fig_scale)
    for name, path, color in zip(opt_names, all_paths, colors):
        if name in optimizers:
            p = path[:,:iterations]
            ax.plot([], [], color=color, label=name, lw=3*fig_scale, linestyle='-')
            ax.quiver(p[0,:-1], p[1,:-1], p[0,1:]-p[0,:-1], p[1,1:]-p[1,:-1], scale_units='xy', angles='xy', scale=1, color=color, lw=4)


    ax.set_xlim((x_min, x_max))
    ax.set_ylim((y_min, y_max))
    ax.legend(loc='lower left', prop={'size': 15*fig_scale}) 
    ax.set_xticks([])
    ax.set_yticks([])
    plt.tight_layout()

from decimal import *
from matplotlib.colors import LogNorm

# Training for momentum
all_lr_paths = []
lr_range = [0.005 * i for i in range(0,10)]
for lr in lr_range:
    opt = tf.optimizers.SGD(lr, nesterov=False)

    x_init = 0.8
    x = tf.compat.v1.get_variable('x', dtype=tf.float32, initializer=tf.constant(x_init))
    y_init = 1.6
    y = tf.compat.v1.get_variable('y', dtype=tf.float32, initializer=tf.constant(y_init))

    x_history = []
    y_history = []
    z_prev = 0.0
    max_steps = 100
    for step in range(max_steps):
        with tf.GradientTape() as g:
            z = f(x, y)
            x_history.append(x.numpy())
            y_history.append(y.numpy())
            dz_dx, dz_dy = g.gradient(z, [x, y])
            opt.apply_gradients(zip([dz_dx, dz_dy], [x, y]))

    if np.abs(z_prev - z.numpy()) < 1e-6:
        break
    z_prev = z.numpy()
    x_history = np.array(x_history)
    y_history = np.array(y_history)
    path = np.concatenate((np.expand_dims(x_history, 1), np.expand_dims(y_history, 1)), axis=1).T
    all_lr_paths.append(path)
    
# Plotting
number_of_points = 50
margin = 4.5
minima = np.array([3., .5])
minima_ = minima.reshape(-1, 1)
x_min = 0. - 2
x_max = 0. + 3.5
y_min = 0. - 3.5
y_max = 0. + 2
x_points = np.linspace(x_min, x_max, number_of_points) 
y_points = np.linspace(y_min, y_max, number_of_points)
x_mesh, y_mesh = np.meshgrid(x_points, y_points)
z = np.array([f(xps, yps) for xps, yps in zip(x_mesh, y_mesh)])

def plot_learning_rate_optimizers(ax, iterations, lr):
    ax.contour(x_mesh, y_mesh, z, levels=np.logspace(-0.5, 5, 25), norm=LogNorm(), cmap=plt.cm.jet, linewidths=fig_scale, zorder=-1)
    ax.plot(*minima, 'r*', markersize=20*fig_scale)
    for path, lrate in zip(all_lr_paths, lr_range):
        if round(lrate,3) == lr:
            p = path[:,:iterations]
            ax.plot([], [], color='b', label="Learning rate {}".format(lr), lw=3*fig_scale, linestyle='-')
            ax.quiver(p[0,:-1], p[1,:-1], p[0,1:]-p[0,:-1], p[1,1:]-p[1,:-1], scale_units='xy', angles='xy', scale=1, color='b', lw=4)


    ax.set_xlim((x_min, x_max))
    ax.set_ylim((y_min, y_max))
    ax.legend(loc='lower left', prop={'size': 15*fig_scale}) 
    ax.set_xticks([])
    ax.set_yticks([])
    plt.tight_layout()

WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.
WARNING:absl:At this time, the v2.11+ optimizer `tf.keras.optimizers.SGD` runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at `tf.keras.optimizers.legacy.SGD`.

Optimizers#

SGD with learning rate schedules#

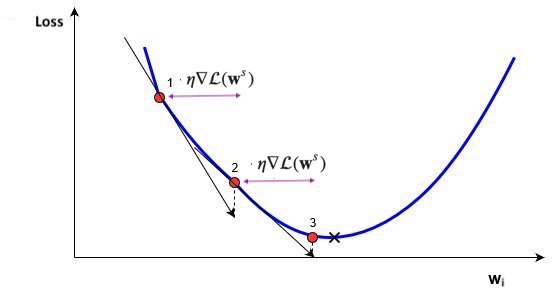
Using a constant learning $\eta$ rate for weight updates $\mathbf{w}_{(s+1)} = \mathbf{w}_s-\eta\nabla \mathcal{L}(\mathbf{w}_s)$ is not ideal
- You would need to ‘magically’ know the right value

import ipywidgets as widgets
from ipywidgets import interact, interact_manual

@interact
def plot_lr(iterations=(1,100,1), learning_rate=(0.005,0.04,0.005)):
    fig, ax = plt.subplots(figsize=(6*fig_scale,4*fig_scale))
    plot_learning_rate_optimizers(ax,iterations,round(learning_rate,3))
    
if not interactive:
    plot_lr(iterations=50, learning_rate=0.02)

SGD with learning rate schedules#

Learning rate decay/annealing with decay rate $k$
- E.g. exponential ($\eta_{s+1} = \eta_{0} e^{-ks}$), inverse-time ($\eta_{s+1} = \frac{\eta_{0}}{1+ks}$),…
Cyclical learning rates
- Change from small to large: hopefully in ‘good’ region long enough before diverging
- Warm restarts: aggressive decay + reset to initial learning rate

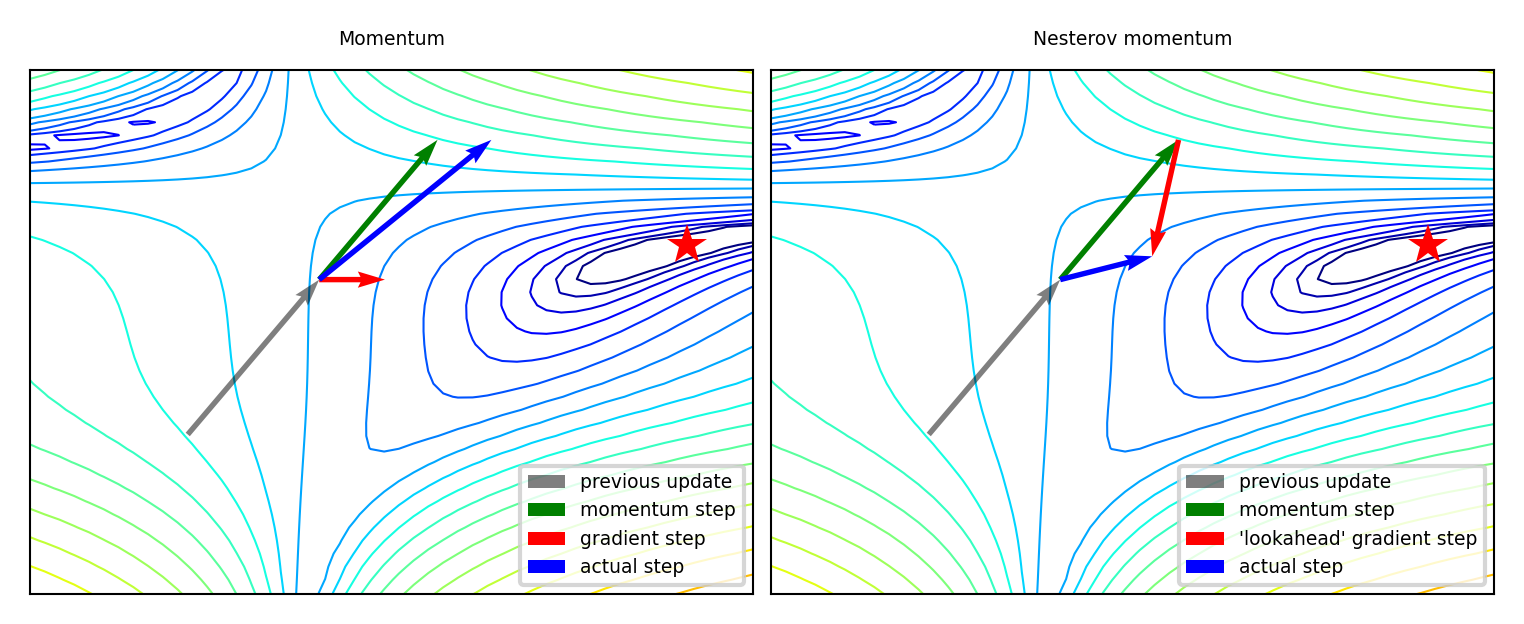
Momentum#

Imagine a ball rolling downhill: accumulates momentum, doesn’t exactly follow steepest descent
- Reduces oscillation, follows larger (consistent) gradient of the loss surface
Adds a velocity vector $\mathbf{v}$ with momentum $\gamma$ (e.g. 0.9, or increase from $\gamma=0.5$ to $\gamma=0.99$) $$\mathbf{w}_{(s+1)} = \mathbf{w}_{(s)} + \mathbf{v}_{(s)} \qquad \text{with} \qquad \color{blue}{\mathbf{v}_{(s)}} = \color{green}{\gamma \mathbf{v}_{(s-1)}} - \color{red}{\eta \nabla \mathcal{L}(\mathbf{w}_{(s)})}$$
Nesterov momentum: Look where momentum step would bring you, compute gradient there
- Responds faster (and reduces momentum) when the gradient changes $$\color{blue}{\mathbf{v}_{(s)}} = \color{green}{\gamma \mathbf{v}_{(s-1)}} - \color{red}{\eta \nabla \mathcal{L}(\mathbf{w}_{(s)} + \gamma \mathbf{v}_{(s-1)})}$$

../_images/43695b436cee2299ed80065ee7d60c4e1bfa6e9c42d6b403e683f8245fb05860.png

Momentum in practice#

Adaptive gradients#

‘Correct’ the learning rate for each $w_i$ based on specific local conditions (layer depth, fan-in,…)
Adagrad: scale $\eta$ according to squared sum of previous gradients $G_{i,(s)} = \sum_{t=1}^s \nabla \mathcal{L}(w_{i,(t)})^2$
- Update rule for $w_i$. Usually $\epsilon=10^{-7}$ (avoids division by 0), $\eta=0.001$. $$w_{i,(s+1)} = w_{i,(s)} - \frac{\eta}{\sqrt{G_{i,(s)}+\epsilon}} \nabla \mathcal{L}(w_{i,(s)})$$
RMSProp: use moving average of squared gradients $m_{i,(s)} = \gamma m_{i,(s-1)} + (1-\gamma) \nabla \mathcal{L}(w_{i,(s)})^2$
- Avoids that gradients dwindle to 0 as $G_{i,(s)}$ grows. Usually $\gamma=0.9, \eta=0.001$ $$w_{i,(s+1)} = w_{i,(s)}- \frac{\eta}{\sqrt{m_{i,(s)}+\epsilon}} \nabla \mathcal{L}(w_{i,(s)})$$

Adam (Adaptive moment estimation)#

Adam: RMSProp + momentum. Adds moving average for gradients as well ($\gamma_2$ = momentum):
- Adds a bias correction to avoid small initial gradients: $\hat{m}_{i,(s)} = \frac{m_{i,(s)}}{1-\gamma}$ and $\hat{g}_{i,(s)} = \frac{g_{i,(s)}}{1-\gamma_2}$ $$g_{i,(s)} = \gamma_2 g_{i,(s-1)} + (1-\gamma_2) \nabla \mathcal{L}(w_{i,(s)})$$w_{i,(s+1)} = w_{i,(s)}- \frac{\eta}{\sqrt{\hat{m}_{i,(s)}+\epsilon}} \hat{g}_{i,(s)}$$
Adamax: Idem, but use max() instead of moving average: $u_{i,(s)} = max(\gamma u_{i,(s-1)}, |\mathcal{L}(w_{i,(s)})|)$ $$w_{i,(s+1)} = w_{i,(s)}- \frac{\eta}{u_{i,(s)}} \hat{g}_{i,(s)}$$

SGD Optimizer Zoo#

RMSProp often works well, but do try alternatives. For even more optimizers, see here.

Neural networks in practice#

There are many practical courses on training neural nets. E.g.:
- With TensorFlow: https://www.tensorflow.org/resources/learn-ml
- With PyTorch: fast.ai course, https://pytorch.org/tutorials/
Here, we’ll use Keras, a general API for building neural networks
- Default API for TensorFlow, also has backends for CNTK, Theano
Focus on key design decisions, evaluation, and regularization
Running example: Fashion-MNIST
- 28x28 pixel images of 10 classes of fashion items

../_images/8e2c6308ea0cf531c830823a8530f07e5433ad87c5aaf279d16a78876504edd7.png

Building the network#

We first build a simple sequential model (no branches)
Input layer (‘input_shape’): a flat vector of 28*28=784 nodes
- We’ll see how to properly deal with images later
Two dense hidden layers: 512 nodes each, ReLU activation
- Glorot weight initialization is applied by default
Output layer: 10 nodes (for 10 classes) and softmax activation

network = models.Sequential()
network.add(layers.Dense(512, activation='relu', kernel_initializer='he_normal', input_shape=(28 * 28,)))
network.add(layers.Dense(512, activation='relu', kernel_initializer='he_normal'))
network.add(layers.Dense(10, activation='softmax'))

Model summary#

Lots of parameters (weights and biases) to learn!
- hidden layer 1 : (28 * 28 + 1) * 512 = 401920
- hidden layer 2 : (512 + 1) * 512 = 262656
- output layer: (512 + 1) * 10 = 5130

network.summary()

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense (Dense)               (None, 512)               401920    
                                                                 
 dense_1 (Dense)             (None, 512)               262656    
                                                                 
 dense_2 (Dense)             (None, 10)                5130      
                                                                 
=================================================================
Total params: 669706 (2.55 MB)
Trainable params: 669706 (2.55 MB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________

Choosing loss, optimizer, metrics#

Loss function
- Cross-entropy (log loss) for multi-class classification ($y_{true}$ is one-hot encoded)
- Use binary crossentropy for binary problems (single output node)
- Use sparse categorical crossentropy if $y_{true}$ is label-encoded (1,2,3,…)
Optimizer
- Any of the optimizers we discussed before. RMSprop usually works well.
Metrics
- To monitor performance during training and testing, e.g. accuracy

# Shorthand
network.compile(loss='categorical_crossentropy', optimizer='rmsprop', metrics=['accuracy'])
# Detailed
network.compile(loss=CategoricalCrossentropy(label_smoothing=0.01),
                optimizer=RMSprop(learning_rate=0.001, momentum=0.0)
                metrics=[Accuracy()])

Preprocessing: Normalization, Reshaping, Encoding#

Always normalize (standardize or min-max) the inputs. Mean should be close to 0.
- Avoid that some inputs overpower others
- Speed up convergence
  - Gradients of activation functions $\frac{\partial a_{h}}{\partial z_{h}}$ are (near) 0 for large inputs
  - If some gradients become much larger than others, SGD will start zig-zagging
Reshape the data to fit the shape of the input layer, e.g. (n, 28*28) or (n, 28,28)
- Tensor with instances in first dimension, rest must match the input layer
In multi-class classification, every class is an output node, so one-hot-encode the labels
- e.g. class ‘4’ becomes [0,0,0,0,1,0,0,0,0,0]

X = X.astype('float32') / 255
X = X.reshape((60000, 28 * 28))
y = to_categorical(y)

Choosing training hyperparameters#

Number of epochs: enough to allow convergence
- Too much: model starts overfitting (or just wastes time)
Batch size: small batches (e.g. 32, 64,… samples) often preferred
- ‘Noisy’ training data makes overfitting less likely
  - Larger batches generalize less well (‘generalization gap’)
- Requires less memory (especially in GPUs)
- Large batches do speed up training, may converge in fewer epochs
Batch size interacts with learning rate
- Instead of shrinking the learning rate you can increase batch size

history = network.fit(X_train, y_train, epochs=3, batch_size=32);

2024-03-17 20:49:51.036237: I tensorflow/core/grappler/optimizers/custom_graph_optimizer_registry.cc:117] Plugin optimizer for device_type GPU is enabled.

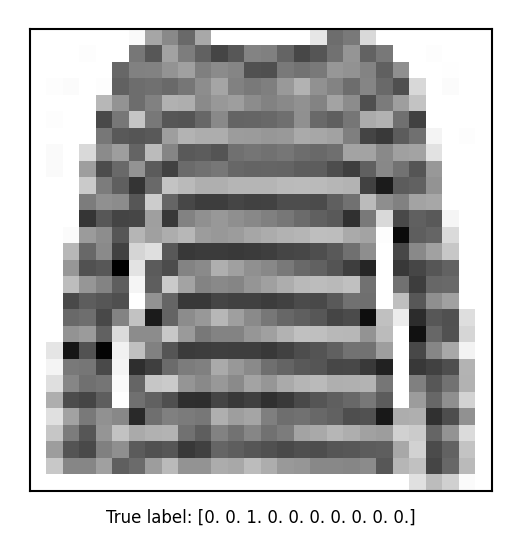
Predictions and evaluations#

We can now call predict to generate predictions, and evaluate the trained model on the entire test set

network.predict(X_test)
test_loss, test_acc = network.evaluate(X_test, y_test)

[0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]

../_images/4e0d14858c38c79c717868a2f53d67a35fb18f9f2e219448e9d86ed9701db27c.png

Test accuracy: 0.7547000050544739

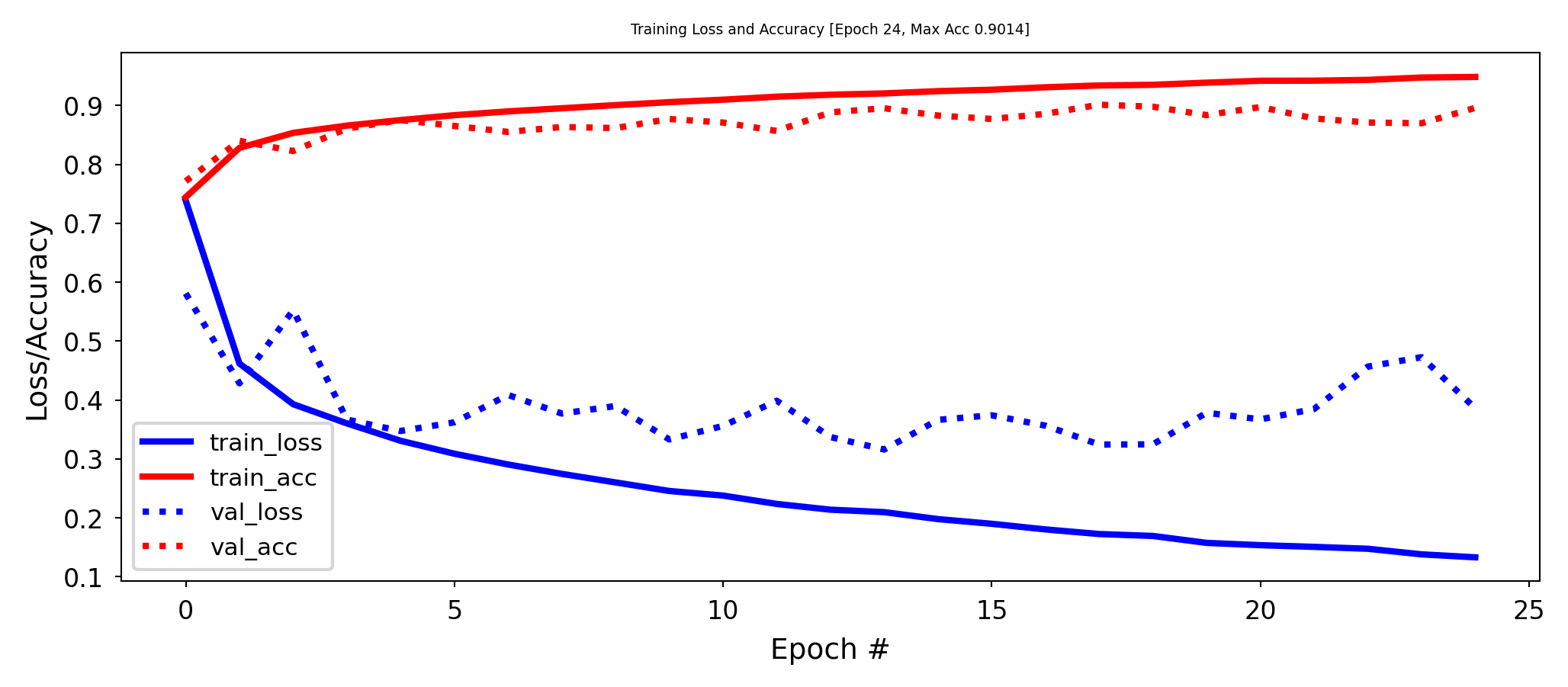
Model selection#

How many epochs do we need for training?
Train the neural net and track the loss after every iteration on a validation set
- You can add a callback to the fit version to get info on every epoch
Best model after a few epochs, then starts overfitting

Show code cell source Hide code cell source

from tensorflow.keras.callbacks import Callback
from IPython.display import clear_output

# For plotting the learning curve in real time
class TrainingPlot(Callback):
    
    # This function is called when the training begins
    def on_train_begin(self, logs={}):
        # Initialize the lists for holding the logs, losses and accuracies
        self.losses = []
        self.acc = []
        self.val_losses = []
        self.val_acc = []
        self.logs = []
        self.max_acc = 0
    
    # This function is called at the end of each epoch
    def on_epoch_end(self, epoch, logs={}):
        
        # Append the logs, losses and accuracies to the lists
        self.logs.append(logs)
        self.losses.append(logs.get('loss'))
        self.acc.append(logs.get('accuracy'))
        self.val_losses.append(logs.get('val_loss'))
        self.val_acc.append(logs.get('val_accuracy'))
        self.max_acc = max(self.max_acc, logs.get('val_accuracy'))
        
        # Before plotting ensure at least 2 epochs have passed
        if len(self.losses) > 1:
            
            # Clear the previous plot
            clear_output(wait=True)
            N = np.arange(0, len(self.losses))
            
            # Plot train loss, train acc, val loss and val acc against epochs passed
            plt.figure(figsize=(8,3))
            plt.plot(N, self.losses, lw=2, c="b", linestyle="-", label = "train_loss")
            plt.plot(N, self.acc, lw=2, c="r", linestyle="-", label = "train_acc")
            plt.plot(N, self.val_losses, lw=2, c="b", linestyle=":", label = "val_loss")
            plt.plot(N, self.val_acc, lw=2, c="r", linestyle=":", label = "val_acc")
            plt.title("Training Loss and Accuracy [Epoch {}, Max Acc {:.4f}]".format(epoch, self.max_acc))
            plt.xlabel("Epoch #", fontsize=18*fig_scale)
            plt.ylabel("Loss/Accuracy", fontsize=18*fig_scale)
            plt.legend(prop={'size': 15*fig_scale})
            plt.tick_params(axis='both', labelsize=16*fig_scale)
            plt.show()

../_images/12b6d032e5803b663d2b3e71c9c9e43338619554f3c9ee9f94a9526aa89401a4.png

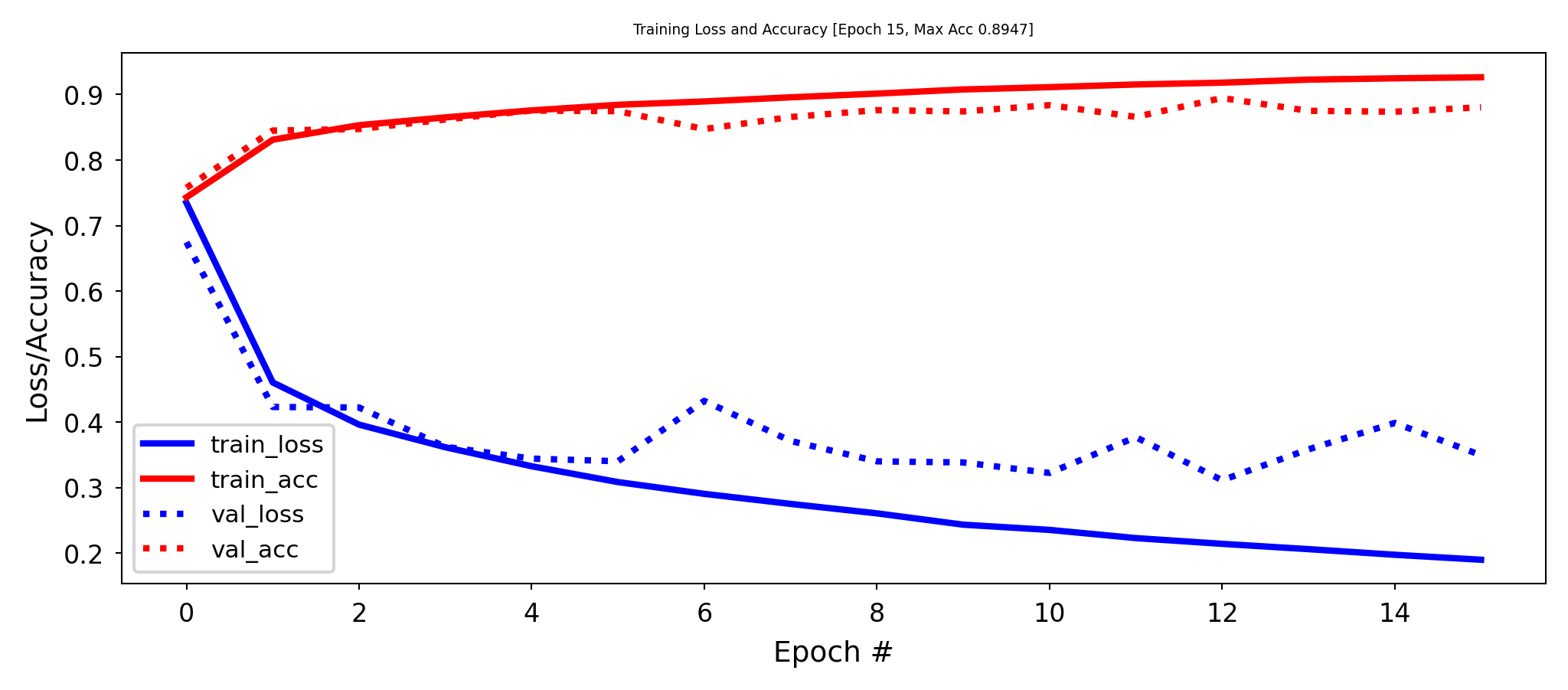
Early stopping#

Stop training when the validation loss (or validation accuracy) no longer improves
Loss can be bumpy: use a moving average or wait for $k$ steps without improvement

earlystop = callbacks.EarlyStopping(monitor='val_loss', patience=3)
model.fit(x_train, y_train, epochs=25, batch_size=512, callbacks=[earlystop])

../_images/beac6c0b01a03042b29c067e29e1967de494d977d5fc543eb3394877217d6faa.png

Regularization and memorization capacity#

The number of learnable parameters is called the model capacity
A model with more parameters has a higher memorization capacity
- Too high capacity causes overfitting, too low causes underfitting
- In the extreme, the training set can be ‘memorized’ in the weights
Smaller models are forced it to learn a compressed representation that generalizes better
- Find the sweet spot: e.g. start with few parameters, increase until overfitting stars.
Example: 256 nodes in first layer, 32 nodes in second layer, similar performance

../_images/40708cfcd5990467a487484a95c818c3c264dd9e95475c817ae065f684704b40.png

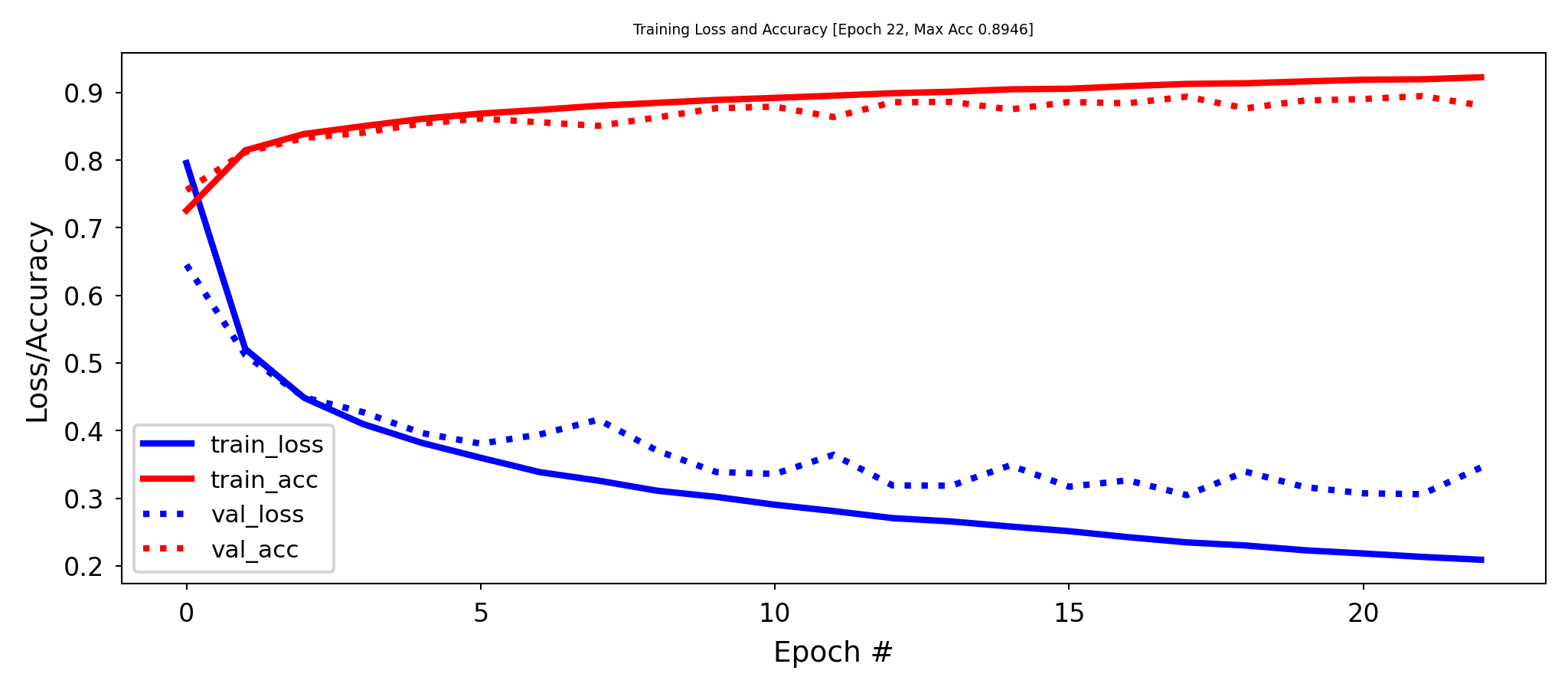
Information bottleneck#

If a layer is too narrow, it will lose information that can never be recovered by subsequent layers
Information bottleneck theory defines a bound on the capacity of the network
Imagine that you need to learn 10 outputs (e.g. classes) and your hidden layer has 2 nodes
- This is like trying to learn 10 hyperplanes from a 2-dimensional representation
Example: bottleneck of 2 nodes, no overfitting, much higher training loss

../_images/ac8e8e7d630544e849c21d898eee86ea2dcb4d6b58964c9fca971cb0092bac91.png

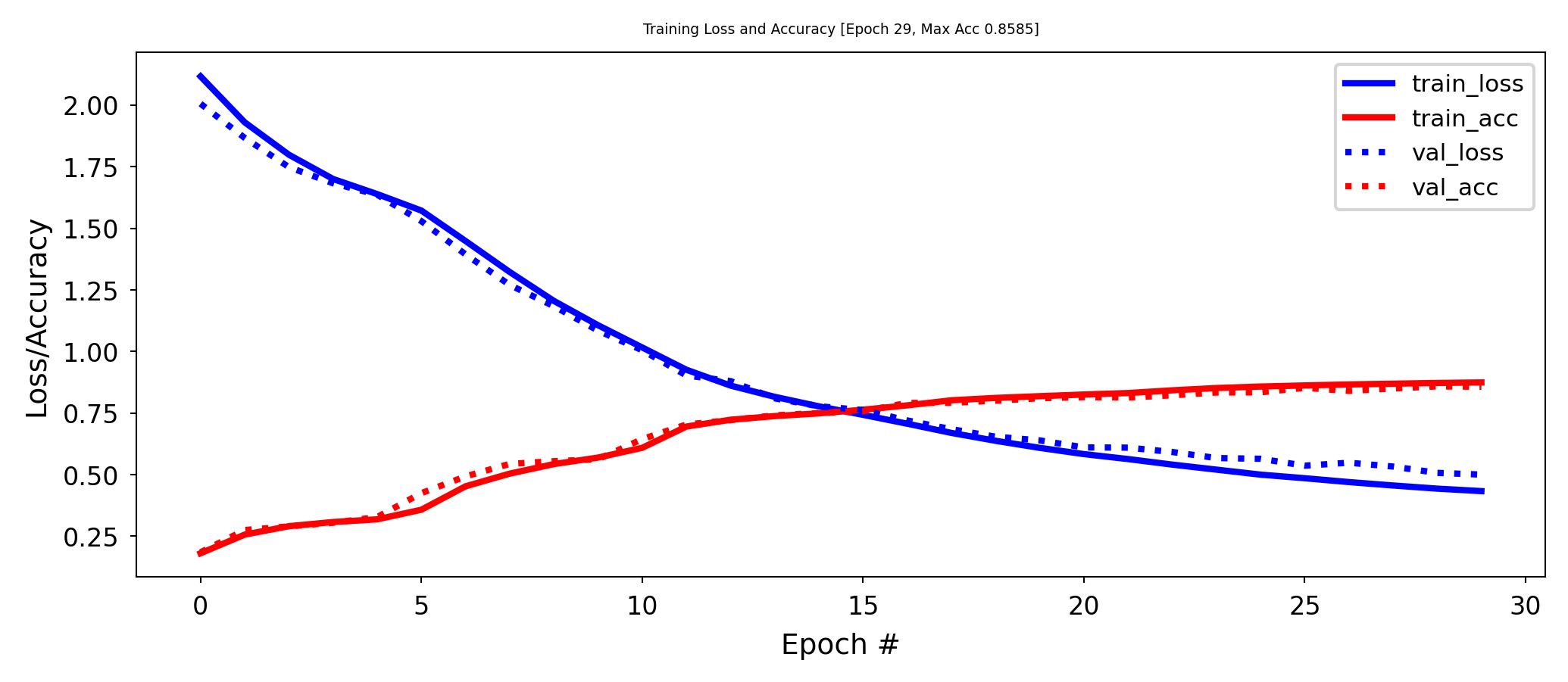
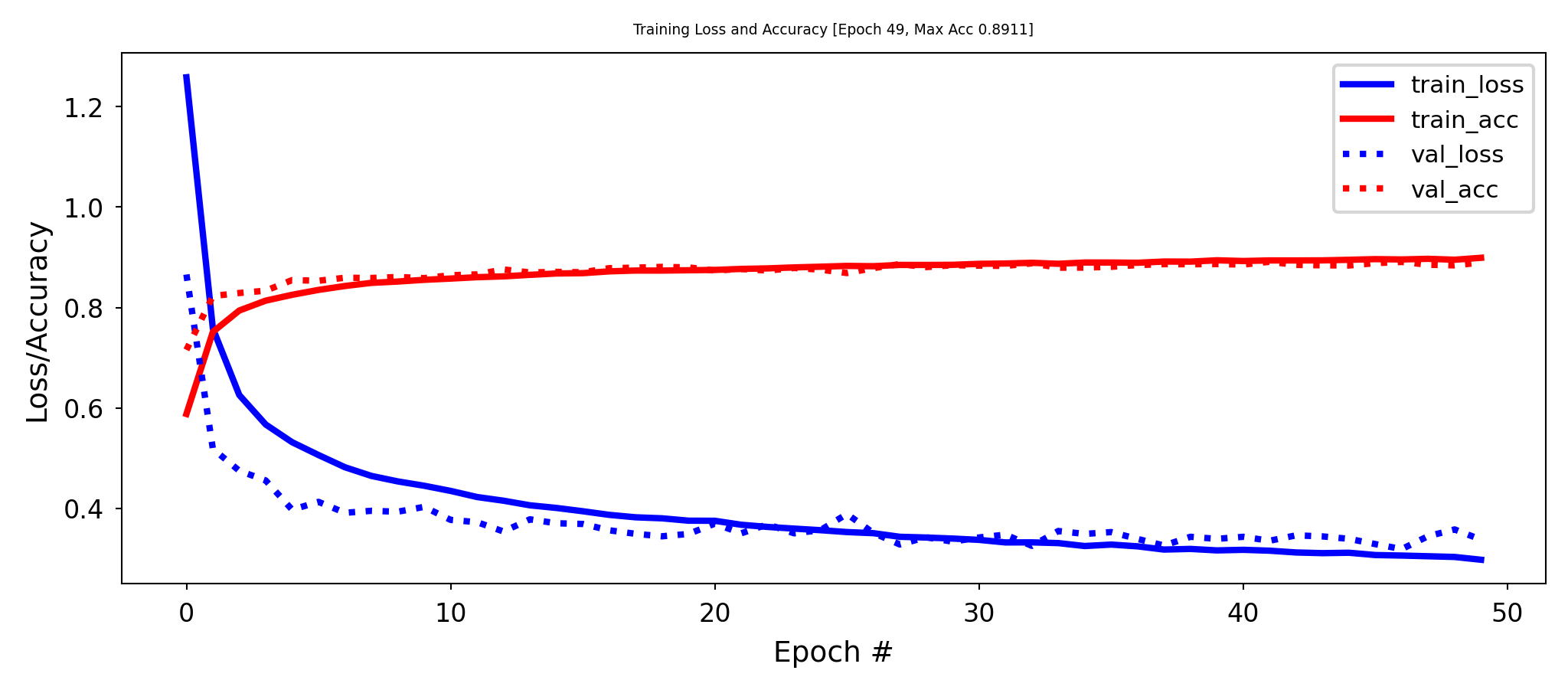
Weight regularization (weight decay)#

As we did many times before, we can also add weight regularization to our loss function

L1 regularization: leads to sparse networks with many weights that are 0
L2 regularization: leads to many very small weights

network = models.Sequential()
network.add(layers.Dense(256, activation='relu', kernel_regularizer=regularizers.l2(0.001), input_shape=(28 * 28,)))
network.add(layers.Dense(128, activation='relu', kernel_regularizer=regularizers.l2(0.001)))

../_images/6688bbea655519aa01ce3d28d088451ab3c8d875830a2b05ff43ceb53eb761c9.png

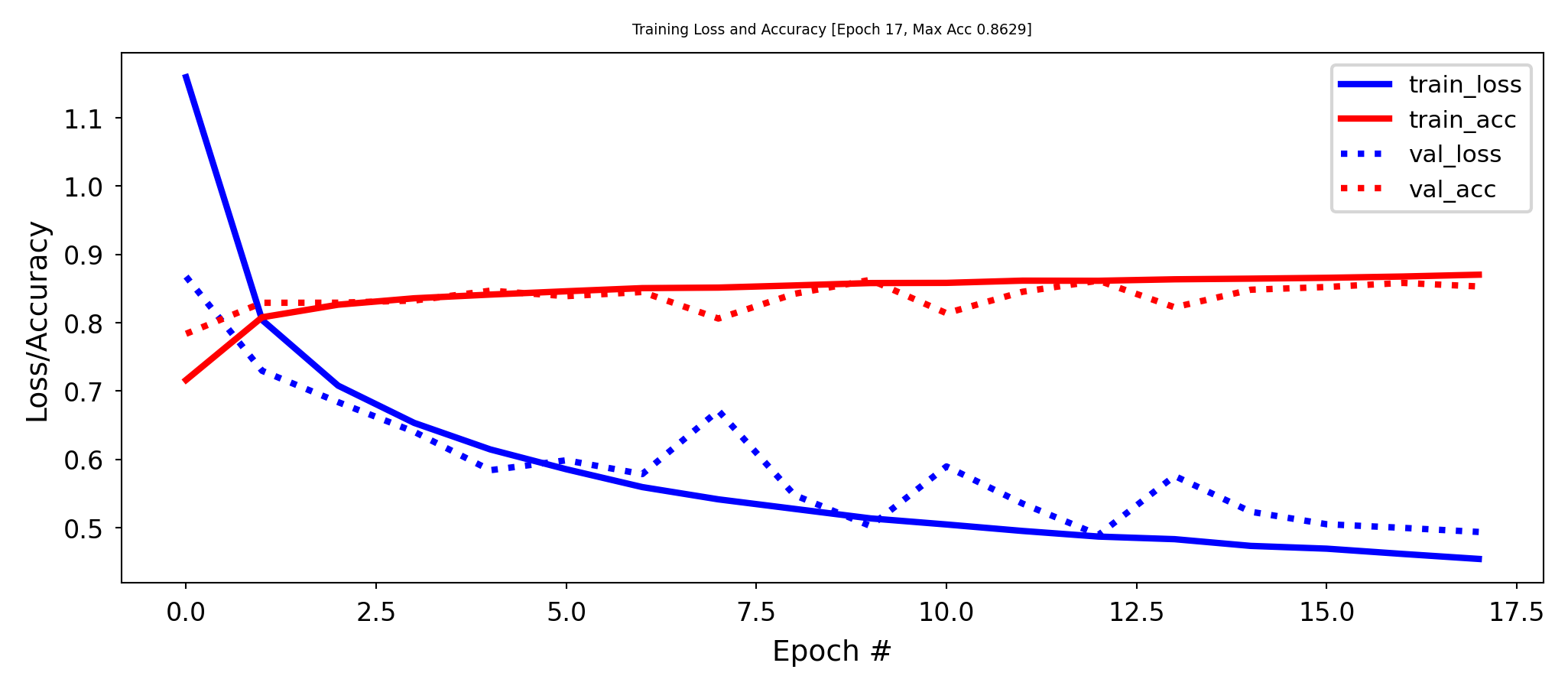
Dropout#

Every iteration, randomly set a number of activations $a_i$ to 0
Dropout rate : fraction of the outputs that are zeroed-out (e.g. 0.1 - 0.5)
Idea: break up accidental non-significant learned patterns
At test time, nothing is dropped out, but the output values are scaled down by the dropout rate
- Balances out that more units are active than during training

Dropout layers#

Dropout is usually implemented as a special layer

network = models.Sequential()
network.add(layers.Dense(256, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dropout(0.5))
network.add(layers.Dense(32, activation='relu'))
network.add(layers.Dropout(0.5))
network.add(layers.Dense(10, activation='softmax'))

../_images/ad42b274cd95f9a45824cef9d2acee0a622191d79399984981344084eb6c47e6.png

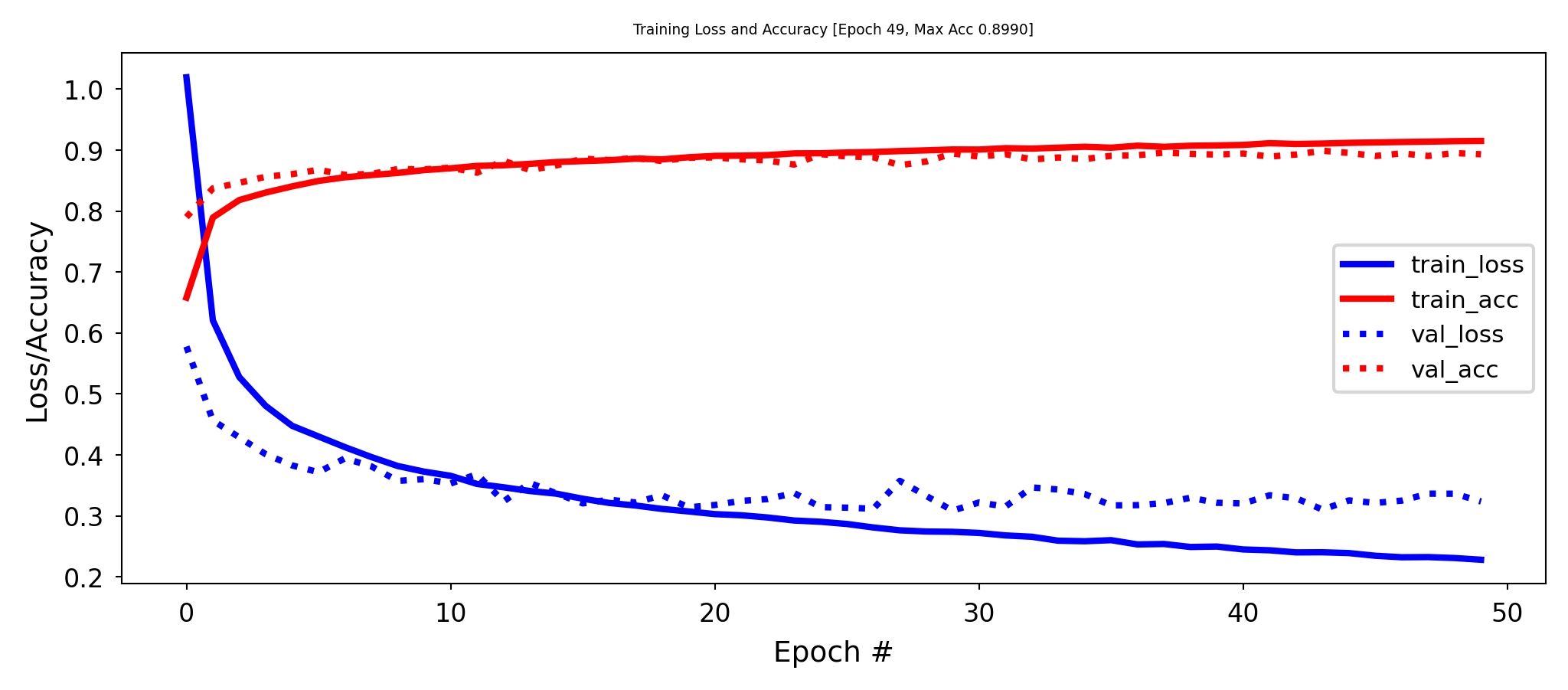
Batch Normalization#

We’ve seen that scaling the input is important, but what if layer activations become very large?
- Same problems, starting deeper in the network
Batch normalization: normalize the activations of the previous layer within each batch
- Within a batch, set the mean activation close to 0 and the standard deviation close to 1
  - Across badges, use exponential moving average of batch-wise mean and variance
- Allows deeper networks less prone to vanishing or exploding gradients

network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.BatchNormalization())
network.add(layers.Dropout(0.5))
network.add(layers.Dense(256, activation='relu'))
network.add(layers.BatchNormalization())
network.add(layers.Dropout(0.5))
network.add(layers.Dense(64, activation='relu'))
network.add(layers.BatchNormalization())
network.add(layers.Dropout(0.5))
network.add(layers.Dense(32, activation='relu'))
network.add(layers.BatchNormalization())
network.add(layers.Dropout(0.5))

../_images/1c5bbd4788e44ac05a8153bf4d86f975b154aa0c4729c746c9141b7c7a0080d7.png

Tuning multiple hyperparameters#

You can wrap Keras models as scikit-learn models and use any tuning technique
Keras also has built-in RandomSearch (and HyperBand and BayesianOptimization - see later)

def make_model(hp):
    m.add(Dense(units=hp.Int('units', min_value=32, max_value=512, step=32)))
    m.compile(optimizer=Adam(hp.Choice('learning rate', [1e-2, 1e-3, 1e-4])))
    return model

from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
clf = KerasClassifier(make_model)
grid = GridSearchCV(clf, param_grid=param_grid, cv=3)

from kerastuner.tuners import RandomSearch
tuner = keras.RandomSearch(build_model, max_trials=5)

Summary#

Neural architectures
Training neural nets
- Forward pass: Tensor operations
- Backward pass: Backpropagation
Neural network design:
- Activation functions
- Weight initialization
- Optimizers
Neural networks in practice
Model selection
- Early stopping
- Memorization capacity and information bottleneck
- L1/L2 regularization
- Dropout
- Batch normalization

Lecture 8. Neural Networks

Contents

Lecture 8. Neural Networks#

Overview#

Architecture#

Basic Architecture#

More layers#

Why layers?#

Other architectures#

Training Neural Nets#

Mini-batch Stochastic Gradient Descent (recap)#

Forward pass#

Tensor operations#

Element-wise operations#

Backward pass (backpropagation)#

Example#

Backpropagation (2)#

Backpropagation (3)#

Summary#

Activation functions for hidden layers#

Effect of activation functions on the gradient#

ReLU vs Tanh#

Activation functions for output layer#

Weight initialization#

Weight initialization: transfer learning#

Optimizers#

SGD with learning rate schedules#

SGD with learning rate schedules#

Momentum#

Momentum in practice#

Adaptive gradients#

Adam (Adaptive moment estimation)#

SGD Optimizer Zoo#

Neural networks in practice#

Building the network#

Model summary#

Choosing loss, optimizer, metrics#

Preprocessing: Normalization, Reshaping, Encoding#

Choosing training hyperparameters#

Predictions and evaluations#

Model selection#

Early stopping#

Regularization and memorization capacity#

Information bottleneck#

Weight regularization (weight decay)#

Dropout#

Dropout layers#

Batch Normalization#

Tuning multiple hyperparameters#

Summary#