Lecture 6. Data preprocessing#
Real-world machine learning pipelines
Joaquin Vanschoren
Show code cell source
# Auto-setup when running on Google Colab
import os
if 'google.colab' in str(get_ipython()) and not os.path.exists('/content/master'):
!git clone -q https://github.com/ML-course/master.git /content/master
!pip --quiet install -r /content/master/requirements_colab.txt
%cd master/notebooks
# Global imports and settings
%matplotlib inline
from preamble import *
interactive = True # Set to True for interactive plots
if interactive:
fig_scale = 0.9
plt.rcParams.update(print_config)
else: # For printing
fig_scale = 0.35
plt.rcParams.update(print_config)
Data transformations#
Machine learning models make a lot of assumptions about the data
In reality, these assumptions are often violated
We build pipelines that transform the data before feeding it to the learners
Scaling (or other numeric transformations)
Encoding (convert categorical features into numerical ones)
Automatic feature selection
Feature engineering (e.g. binning, polynomial features,…)
Handling missing data
Handling imbalanced data
Dimensionality reduction (e.g. PCA)
Learned embeddings (e.g. for text)
Seek the best combinations of transformations and learning methods
Often done empirically, using cross-validation
Make sure that there is no data leakage during this process!
Scaling#
Use when different numeric features have different scales (different range of values)
Features with much higher values may overpower the others
Goal: bring them all within the same range
Different methods exist
Show code cell source
from sklearn.datasets import fetch_openml
from sklearn.preprocessing import LabelEncoder, MinMaxScaler, StandardScaler, RobustScaler, Normalizer, MaxAbsScaler
import ipywidgets as widgets
from ipywidgets import interact, interact_manual
# Iris dataset with some added noise
def noisy_iris():
iris = fetch_openml("iris", return_X_y=True, as_frame=False)
X, y = iris
np.random.seed(0)
noise = np.random.normal(0, 0.1, 150)
for i in range(4):
X[:, i] = X[:, i] + noise
X[:, 0] = X[:, 0] + 3 # add more skew
label_encoder = LabelEncoder().fit(y)
y = label_encoder.transform(y)
return X, y
scalers = [StandardScaler(), RobustScaler(), MinMaxScaler(), Normalizer(norm='l1'), MaxAbsScaler()]
@interact
def plot_scaling(scaler=scalers):
X, y = noisy_iris()
X = X[:,:2] # Use only first 2 features
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(8*fig_scale, 3*fig_scale))
axes[0].scatter(X[:, 0], X[:, 1], c=y, s=1*fig_scale, cmap="brg")
axes[0].set_xlim(-15, 15)
axes[0].set_ylim(-5, 5)
axes[0].set_title("Original Data")
axes[0].spines['left'].set_position('zero')
axes[0].spines['bottom'].set_position('zero')
X_ = scaler.fit_transform(X)
axes[1].scatter(X_[:, 0], X_[:, 1], c=y, s=1*fig_scale, cmap="brg")
axes[1].set_xlim(-2, 2)
axes[1].set_ylim(-2, 2)
axes[1].set_title(type(scaler).__name__)
axes[1].set_xticks([-1,1])
axes[1].set_yticks([-1,1])
axes[1].spines['left'].set_position('center')
axes[1].spines['bottom'].set_position('center')
for ax in axes:
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
Show code cell source
if not interactive:
plot_scaling(scalers[0])
Why do we need scaling?#
KNN: Distances depend mainly on feature with larger values
SVMs: (kernelized) dot products are also based on distances
Linear model: Feature scale affects regularization
Weights have similar scales, more interpretable
Show code cell source
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.base import clone
# Example by Andreas Mueller, with some tweaks
def plot_2d_classification(classifier, X, fill=False, ax=None, eps=None, alpha=1):
# multiclass
if eps is None:
eps = X.std(axis=0) / 2.
else:
eps = np.array([eps, eps])
if ax is None:
ax = plt.gca()
x_min, x_max = X[:, 0].min() - eps[0], X[:, 0].max() + eps[0]
y_min, y_max = X[:, 1].min() - eps[1], X[:, 1].max() + eps[1]
# these should be 1000 but knn predict is unnecessarily slow
xx = np.linspace(x_min, x_max, 100)
yy = np.linspace(y_min, y_max, 100)
X1, X2 = np.meshgrid(xx, yy)
X_grid = np.c_[X1.ravel(), X2.ravel()]
decision_values = classifier.predict(X_grid)
ax.imshow(decision_values.reshape(X1.shape), extent=(x_min, x_max,
y_min, y_max),
aspect='auto', origin='lower', alpha=alpha, cmap=plt.cm.bwr)
clfs = [KNeighborsClassifier(), SVC(), LinearSVC(), LogisticRegression(C=10)]
@interact
def plot_scaling_effect(classifier=clfs, show_test=[False,True]):
X, y = make_blobs(centers=2, random_state=4, n_samples=50)
X = X * np.array([1000, 1])
y[7], y[27] = 0, 0
X_train, X_test, y_train, y_test = train_test_split(X,y, stratify=y, random_state=1)
clf2 = clone(classifier)
clf_unscaled = classifier.fit(X_train, y_train)
fig, axes = plt.subplots(1, 2, figsize=(7*fig_scale, 3*fig_scale))
axes[0].scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap='bwr', label="train")
axes[0].set_title("Without scaling. Accuracy:{:.2f}".format(clf_unscaled.score(X_test,y_test)))
if show_test: # Hide test data for simplicity
axes[0].scatter(X_test[:, 0], X_test[:, 1], c=y_test, marker='^', cmap='bwr', label="test")
axes[0].legend()
scaler = StandardScaler().fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
clf_scaled = clf2.fit(X_train_scaled, y_train)
axes[1].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1], c=y_train, cmap='bwr', label="train")
axes[1].set_title("With scaling. Accuracy:{:.2f}".format(clf_scaled.score(X_test_scaled,y_test)))
if show_test: # Hide test data for simplicity
axes[1].scatter(X_test_scaled[:, 0], X_test_scaled[:, 1], c=y_test, marker='^', cmap='bwr', label="test")
axes[1].legend()
plot_2d_classification(clf_unscaled, X, ax=axes[0], alpha=.2)
plot_2d_classification(clf_scaled, scaler.transform(X), ax=axes[1], alpha=.3)
Show code cell source
if not interactive:
plot_scaling_effect(classifier=clfs[0], show_test=False)
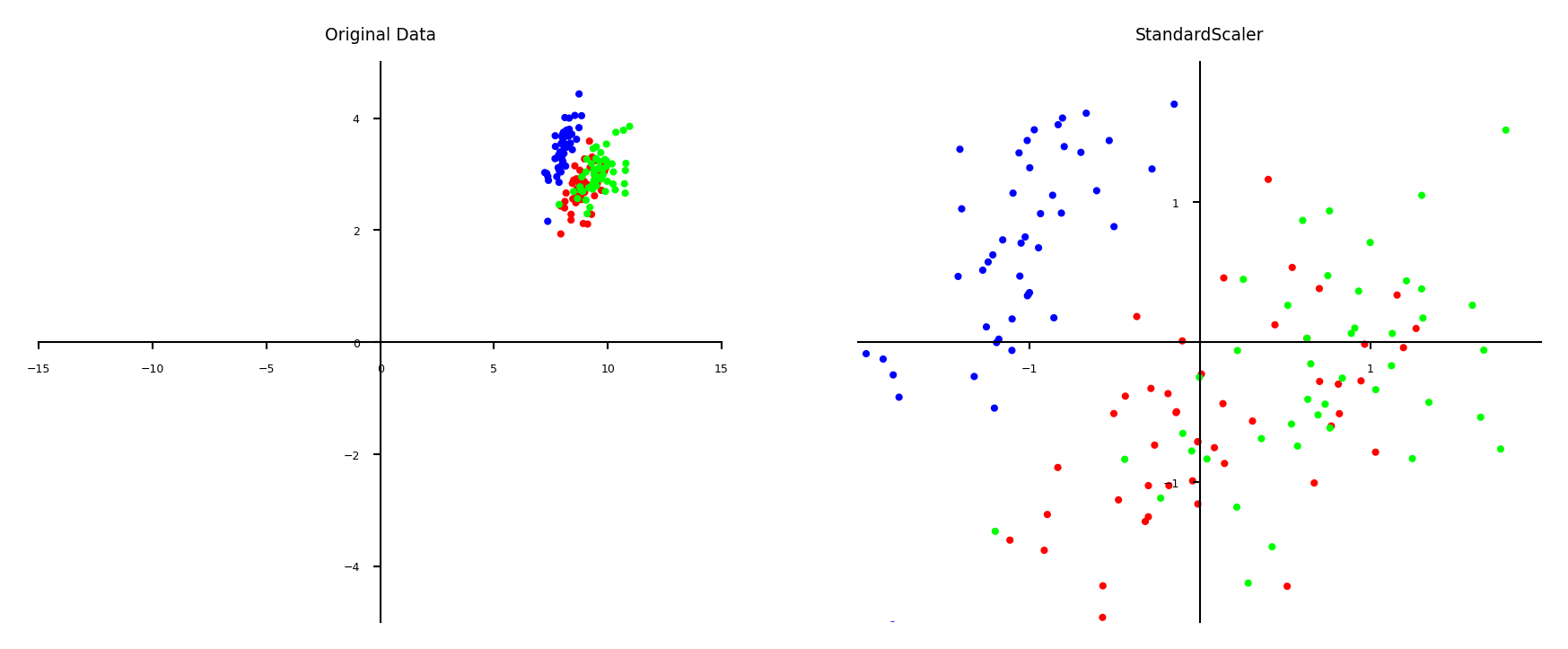
Standard scaling (standardization)#
Generally most useful, assumes data is more or less normally distributed
Per feature, subtract the mean value \(\mu\), scale by standard deviation \(\sigma\)
New feature has \(\mu=0\) and \(\sigma=1\), values can still be arbitrarily large $\(\mathbf{x}_{new} = \frac{\mathbf{x} - \mu}{\sigma}\)$
Show code cell source
plot_scaling(scaler=StandardScaler())
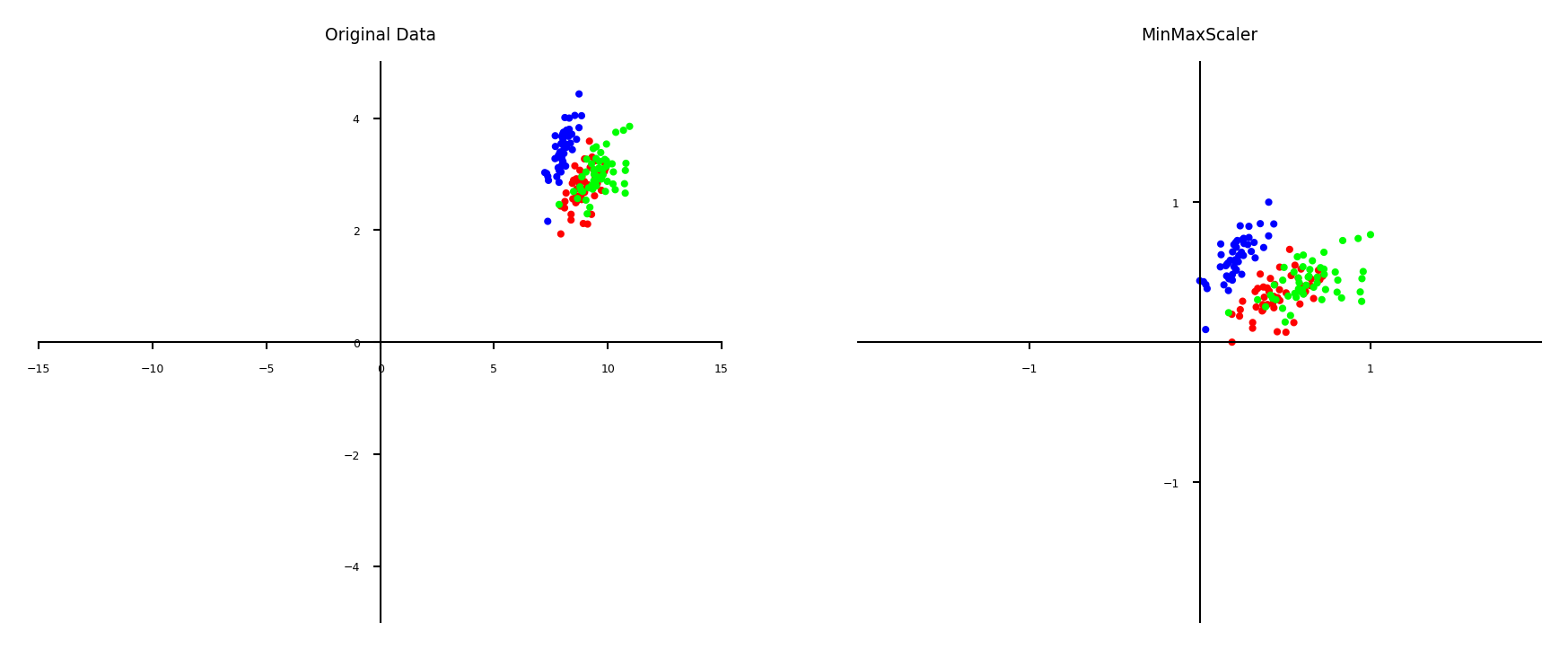
Min-max scaling#
Scales all features between a given \(min\) and \(max\) value (e.g. 0 and 1)
Makes sense if min/max values have meaning in your data
Sensitive to outliers
Show code cell source
plot_scaling(scaler=MinMaxScaler(feature_range=(0, 1)))
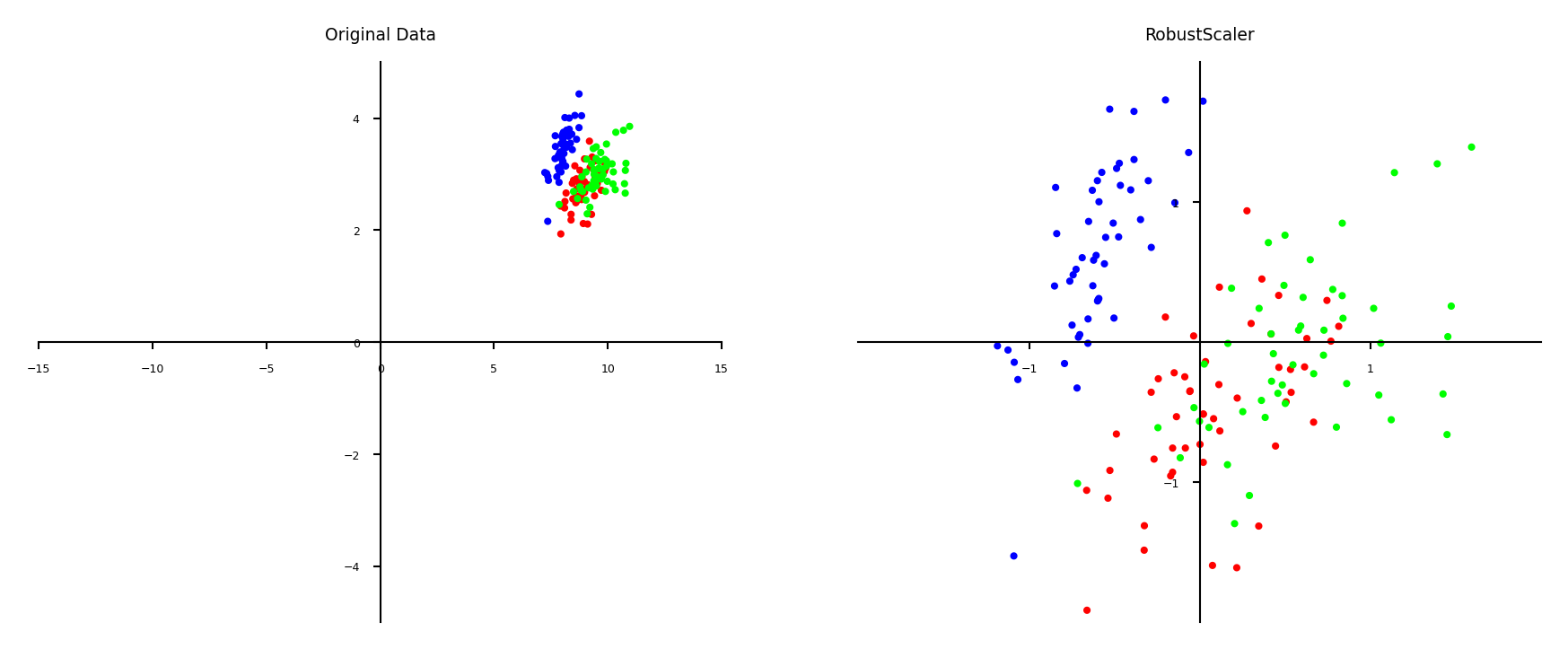
Robust scaling#
Subtracts the median, scales between quantiles \(q_{25}\) and \(q_{75}\)
New feature has median 0, \(q_{25}=-1\) and \(q_{75}=1\)
Similar to standard scaler, but ignores outliers
Show code cell source
plot_scaling(scaler=RobustScaler())
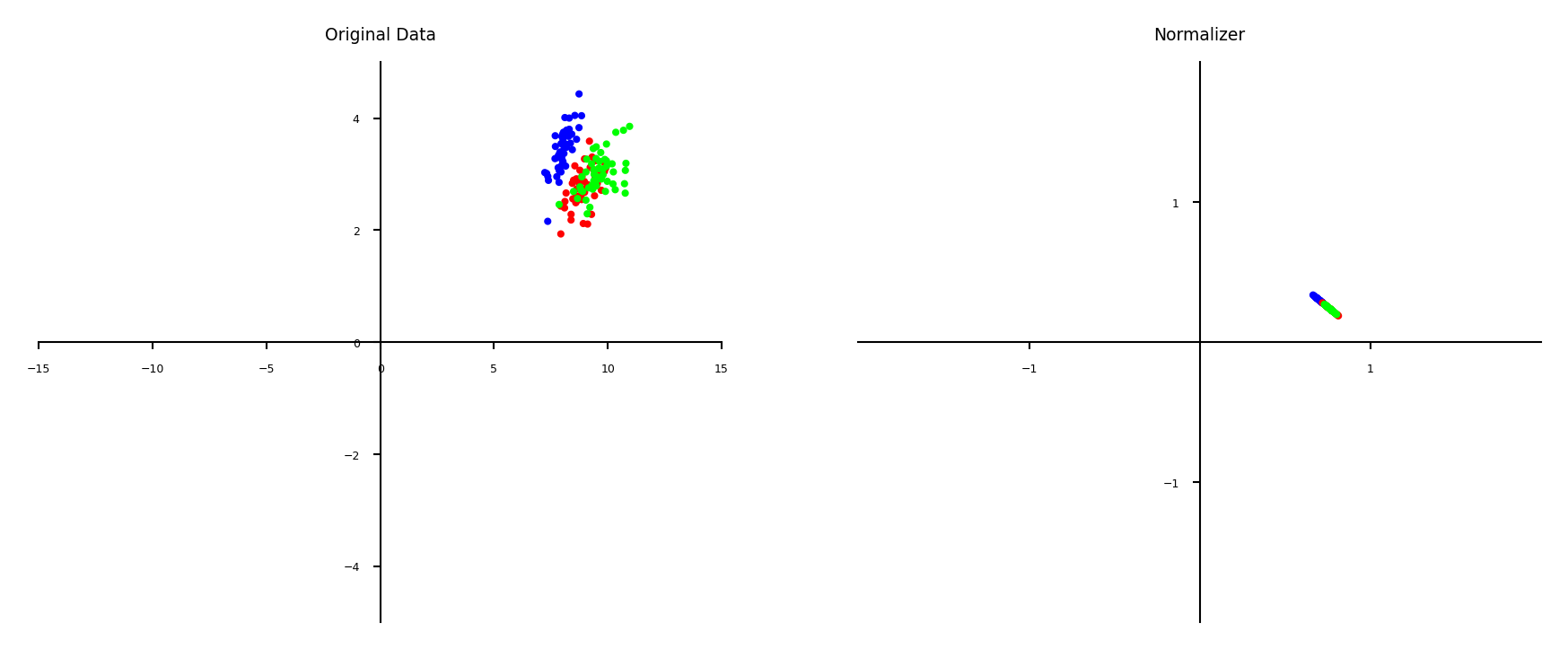
Normalization#
Makes sure that feature values of each point (each row) sum up to 1 (L1 norm)
Useful for count data (e.g. word counts in documents)
Can also be used with L2 norm (sum of squares is 1)
Useful when computing distances in high dimensions
Normalized Euclidean distance is equivalent to cosine similarity
Show code cell source
plot_scaling(scaler=Normalizer(norm='l1'))
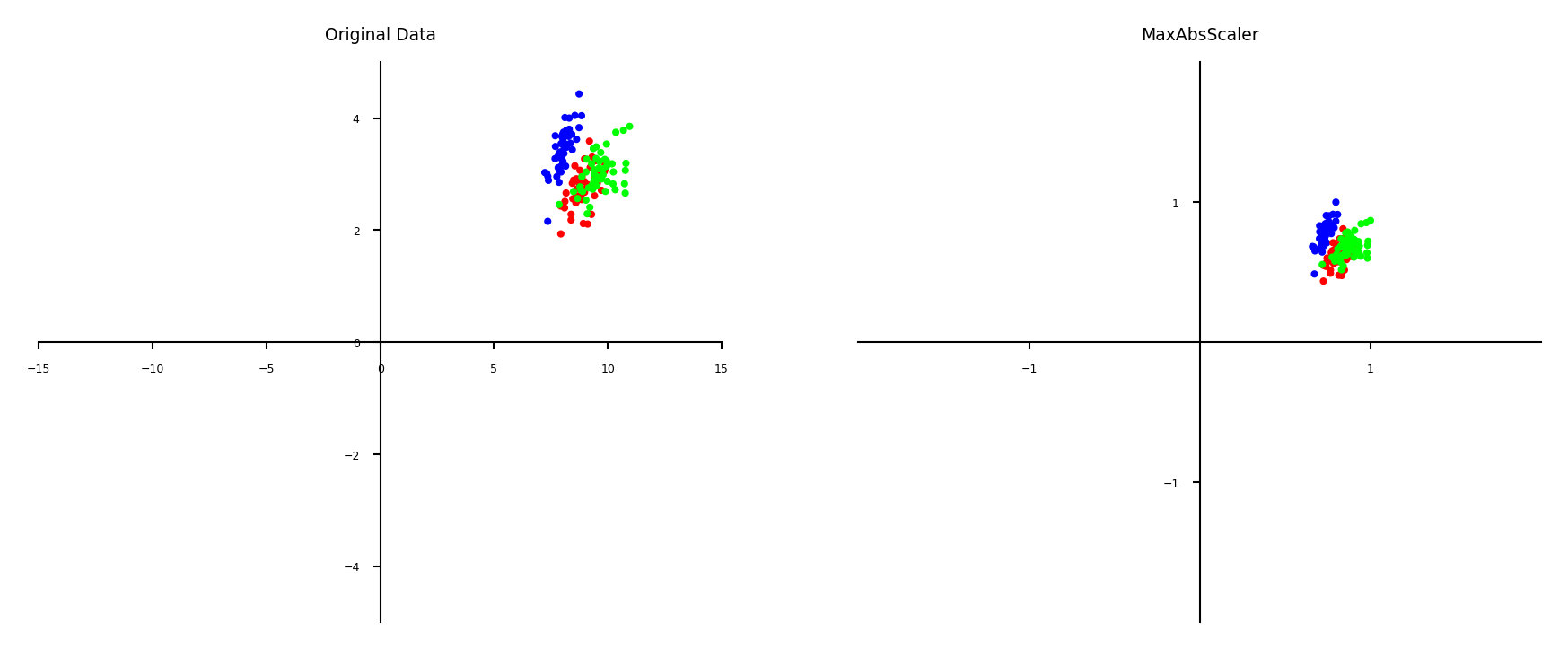
Maximum Absolute scaler#
For sparse data (many features, but few are non-zero)
Maintain sparseness (efficient storage)
Scales all values so that maximum absolute value is 1
Similar to Min-Max scaling without changing 0 values
Show code cell source
plot_scaling(scaler=MaxAbsScaler())
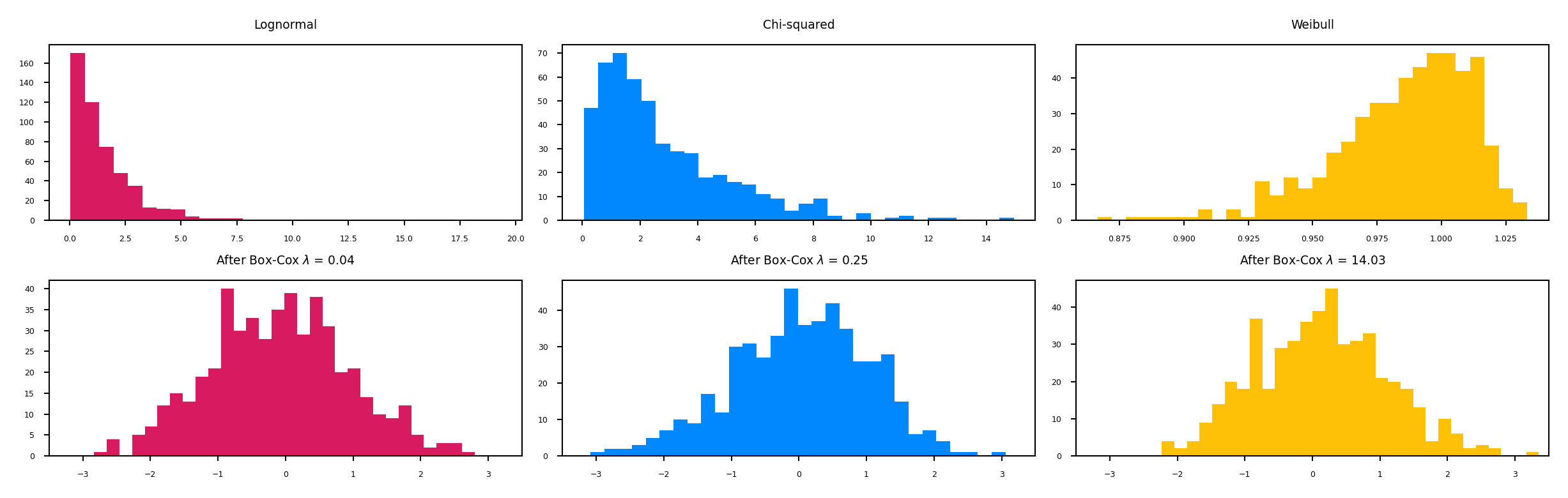
Power transformations#
Some features follow certain distributions
E.g. number of twitter followers is log-normal distributed
Box-Cox transformations transform these to normal distributions (\(\lambda\) is fitted)
Only works for positive values, use Yeo-Johnson otherwise $\(bc_{\lambda}(x) = \begin{cases} log(x) & \lambda = 0\\ \frac{x^{\lambda}-1}{\lambda} & \lambda \neq 0 \\ \end{cases}\)$
Show code cell source
# Adapted from an example by Eric Chang and Nicolas Hug
from sklearn.preprocessing import PowerTransformer
# Power transformer with Box-Cox
bc = PowerTransformer(method='box-cox')
# Generate data
rng = np.random.RandomState(304) # Random number generator
size = (1000, 1)
X_lognormal = rng.lognormal(size=size) # lognormal distribution
X_chisq = rng.chisquare(df=3, size=size) # chi-squared distribution
X_weibull = rng.weibull(a=50, size=size) # weibull distribution
# create plots
distributions = [
('Lognormal', X_lognormal),
('Chi-squared', X_chisq),
('Weibull', X_weibull)
]
colors = ['#D81B60', '#0188FF', '#FFC107']
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(9*fig_scale,2.8*fig_scale))
axes = axes.flatten()
axes_idxs = [(0, 3), (1, 4), (2, 5)]
axes_list = [(axes[i], axes[j]) for (i, j) in axes_idxs]
for distribution, color, axes in zip(distributions, colors, axes_list):
name, X = distribution
X_train, X_test = train_test_split(X, test_size=.5)
# perform power transforms and quantile transform
X_trans_bc = bc.fit(X_train).transform(X_test)
lmbda_bc = round(bc.lambdas_[0], 2)
ax_original, ax_bc = axes
ax_original.hist(X_train, color=color, bins=30)
ax_original.set_title(name)
ax_original.tick_params(axis='both', which='major')
ax_bc.hist(X_trans_bc, color=color, bins=30)
title = 'After {}'.format('Box-Cox')
if lmbda_bc is not None:
title += r' $\lambda$ = {}'.format(lmbda_bc)
ax_bc.set_title(title)
ax_bc.tick_params(axis='both', which='major')
ax_bc.set_xlim([-3.5, 3.5])
plt.tight_layout()
plt.show()
Categorical feature encoding#
Many algorithms can only handle numeric features, so we need to encode the categorical ones
Show code cell source
table_font_size = 20
heading_properties = [('font-size', table_font_size)]
cell_properties = [('font-size', table_font_size)]
dfstyle = [dict(selector="th", props=heading_properties),\
dict(selector="td", props=cell_properties)]
%%HTML
<style>
td {font-size: 10px}
th {font-size: 10px}
.rendered_html table, .rendered_html td, .rendered_html th {
font-size: 20px;
}
</style>
Show code cell source
import pandas as pd
X = pd.DataFrame({'boro': ['Manhattan', 'Queens', 'Manhattan', 'Brooklyn', 'Brooklyn', 'Bronx'],
'salary': [103, 89, 142, 54, 63, 219]})
y = pd.DataFrame({'vegan': [0, 0, 0, 1, 1, 0]})
df = X.copy()
df['vegan'] = y
df.style.set_table_styles(dfstyle)
| boro | salary | vegan | |
|---|---|---|---|
| 0 | Manhattan | 103 | 0 |
| 1 | Queens | 89 | 0 |
| 2 | Manhattan | 142 | 0 |
| 3 | Brooklyn | 54 | 1 |
| 4 | Brooklyn | 63 | 1 |
| 5 | Bronx | 219 | 0 |
Ordinal encoding#
Simply assigns an integer value to each category in the order they are encountered
Only really useful if there exist a natural order in categories
Model will consider one category to be ‘higher’ or ‘closer’ to another
Show code cell source
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OrdinalEncoder
encoder = OrdinalEncoder(dtype=int)
# Encode first feature, rest passthrough
preprocessor = ColumnTransformer(transformers=[('cat', encoder, [0])], remainder='passthrough')
X_ordinal = preprocessor.fit_transform(X,y)
# Convert to pandas for nicer output
df = pd.DataFrame(data=X_ordinal, columns=["boro_ordinal","salary"])
df = pd.concat([X['boro'], df], axis=1)
df.style.set_table_styles(dfstyle)
| boro | boro_ordinal | salary | |
|---|---|---|---|
| 0 | Manhattan | 2 | 103 |
| 1 | Queens | 3 | 89 |
| 2 | Manhattan | 2 | 142 |
| 3 | Brooklyn | 1 | 54 |
| 4 | Brooklyn | 1 | 63 |
| 5 | Bronx | 0 | 219 |
One-hot encoding (dummy encoding)#
Simply adds a new 0/1 feature for every category, having 1 (hot) if the sample has that category
Can explode if a feature has lots of values, causing issues with high dimensionality
What if test set contains a new category not seen in training data?
Either ignore it (just use all 0’s in row), or handle manually (e.g. resample)
Show code cell source
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder(dtype=int)
# Encode first feature, rest passthrough
preprocessor = ColumnTransformer(transformers=[('cat', encoder, [0])], remainder='passthrough')
X_ordinal = preprocessor.fit_transform(X,y)
# Convert to pandas for nicer output
df = pd.DataFrame(data=X_ordinal, columns=["boro_Bronx","boro_Brooklyn","boro_Manhattan","boro_Queens","salary"])
df = pd.concat([X['boro'], df], axis=1)
df.style.set_table_styles(dfstyle)
| boro | boro_Bronx | boro_Brooklyn | boro_Manhattan | boro_Queens | salary | |
|---|---|---|---|---|---|---|
| 0 | Manhattan | 0 | 0 | 1 | 0 | 103 |
| 1 | Queens | 0 | 0 | 0 | 1 | 89 |
| 2 | Manhattan | 0 | 0 | 1 | 0 | 142 |
| 3 | Brooklyn | 0 | 1 | 0 | 0 | 54 |
| 4 | Brooklyn | 0 | 1 | 0 | 0 | 63 |
| 5 | Bronx | 1 | 0 | 0 | 0 | 219 |
Target encoding#
Value close to 1 if category correlates with class 1, close to 0 if correlates with class 0
Preferred when you have lots of category values. It only creates one new feature per class
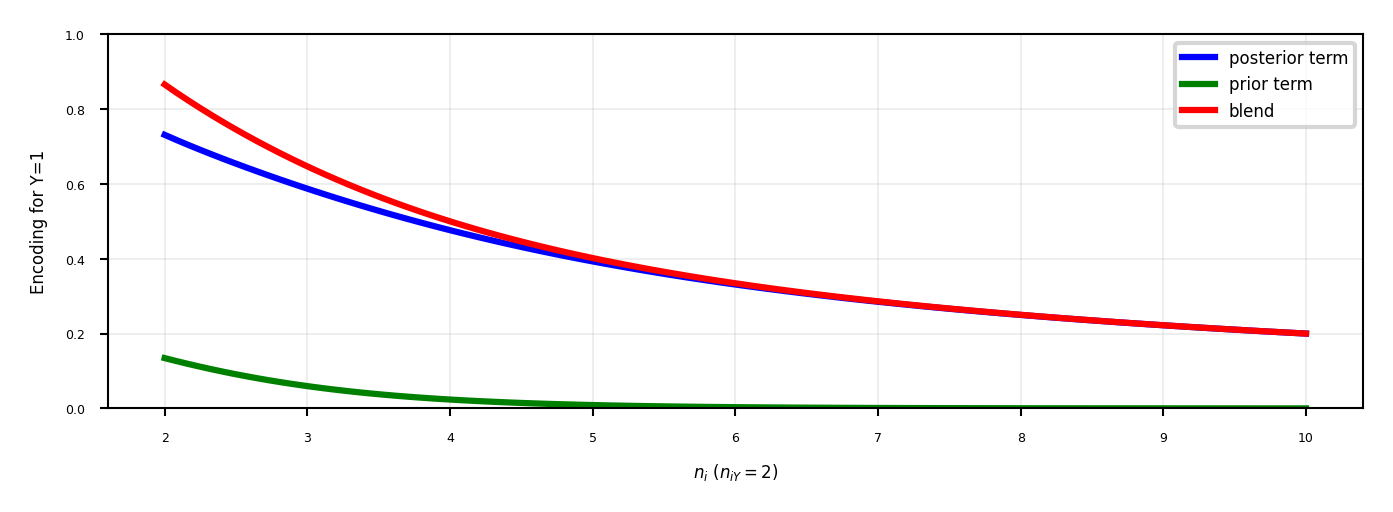
Blends posterior probability of the target \(\frac{n_{iY}}{n_i}\) and prior probability \(\frac{n_Y}{n}\).
\(n_{iY}\): nr of samples with category i and class Y=1, \(n_{i}\): nr of samples with category i
Blending: gradually decrease as you get more examples of category i and class Y=0 $\(Enc(i) = \color{blue}{\frac{1}{1+e^{-(n_{i}-1)}} \frac{n_{iY}}{n_i}} + \color{green}{(1-\frac{1}{1+e^{-(n_{i}-1)}}) \frac{n_Y}{n}}\)$
Same for regression, using \(\frac{n_{iY}}{n_i}\): average target value with category i, \(\frac{n_{Y}}{n}\): overall mean
Show code cell source
# smoothed sigmoid
def sigmoid(x, smoothing=1):
return 1 / (1 + np.exp(-(x-1)/smoothing))
def plot_blend():
n = 20 # 20 points
ny = 10 # 10 points of class Yes
niy = 2 # number of points of category i and class Yes
ni = np.linspace(niy,10,100) # 10 points of category i
fig, ax = plt.subplots(figsize=(6*fig_scale,1.8*fig_scale))
ax.plot(ni,sigmoid(ni)*(niy/ni),lw=1.5,c='b',label='posterior term', linestyle='-')
ax.plot(ni,(1-sigmoid(ni))*(ny/n),lw=1.5,c='g',label='prior term', linestyle='-')
ax.plot(ni,sigmoid(ni)*(niy/ni) + (1-sigmoid(ni))*(ny/n),lw=1.5,c='r',label='blend', linestyle='-')
ax.set_xlabel(r"$n_{i}$ ($n_{iY} = 2$)")
ax.set_ylabel("Encoding for Y=1")
ax.set_ylim(0,1)
plt.grid()
plt.legend();
plot_blend()
Example (category_encoders)#
For Brooklyn, \(n_{iY}=2, n_{i}=2, n_{Y}=2, n=6\)
Would be closer to 1 if there were more examples, all with label 1 $\(Enc(Brooklyn) = \frac{1}{1+e^{-1}} \frac{2}{2} + (1-\frac{1}{1+e^{-1}}) \frac{2}{6} = 0,82\)$
Note: the implementation used here sets \(Enc(i)=\frac{n_Y}{n}\) when \(n_{iY}=1\)
Show code cell source
# Not in sklearn yet, use package category_encoders
from category_encoders import TargetEncoder
encoder = TargetEncoder(return_df=True, smoothing=1, min_samples_leaf=1)
encoder.fit(X, y)
pd_te = encoder.fit_transform(X,y)
# Convert to pandas for nicer output
df = pd.DataFrame(data=pd_te, columns=["boro","salary"]).rename(columns={'boro': 'boro_encoded'})
df = pd.concat([X['boro'], df, y], axis=1)
df.style.set_table_styles(dfstyle)
| boro | boro_encoded | salary | vegan | |
|---|---|---|---|---|
| 0 | Manhattan | 0.089647 | 103 | 0 |
| 1 | Queens | 0.166667 | 89 | 0 |
| 2 | Manhattan | 0.089647 | 142 | 0 |
| 3 | Brooklyn | 0.820706 | 54 | 1 |
| 4 | Brooklyn | 0.820706 | 63 | 1 |
| 5 | Bronx | 0.166667 | 219 | 0 |
In practice (scikit-learn)#
Ordinal encoding, one-hot encoding, target encoding are implemented in scikit-learn
dtype defines that the output should be an integer
ordinal_encoder = OrdinalEncoder(dtype=int)
one_hot_encoder = OneHotEncoder(dtype=int)
target_encoder = TargetEncoder(smooth=0.25)
Target encoding is available in
category_encodersscikit-learn compatible
Also includes other, very specific encoders
target_encoder = TargetEncoder(return_df=True)
All encoders (and scalers) follow the
fit-transformparadigmfitprepares the encoder,transformactually encodes the featuresWe’ll discuss this next
encoder.fit(X, y)
X_encoded = encoder.transform(X,y)
Applying data transformations#
Data transformations should always follow a fit-predict paradigm
Fit the transformer on the training data only
E.g. for a standard scaler: record the mean and standard deviation
Transform (e.g. scale) the training data, then train the learning model
Transform (e.g. scale) the test data, then evaluate the model
Only scale the input features (X), not the targets (y)
If you fit and transform the whole dataset before splitting, you get data leakage
You have looked at the test data before training the model
Model evaluations will be misleading
If you fit and transform the training and test data separately, you distort the data
E.g. training and test points are scaled differently
In practice (scikit-learn)#
# choose scaling method and fit on training data
scaler = StandardScaler()
scaler.fit(X_train)
# transform training and test data
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# calling fit and transform in sequence
X_train_scaled = scaler.fit(X_train).transform(X_train)
# same result, but more efficient computation
X_train_scaled = scaler.fit_transform(X_train)
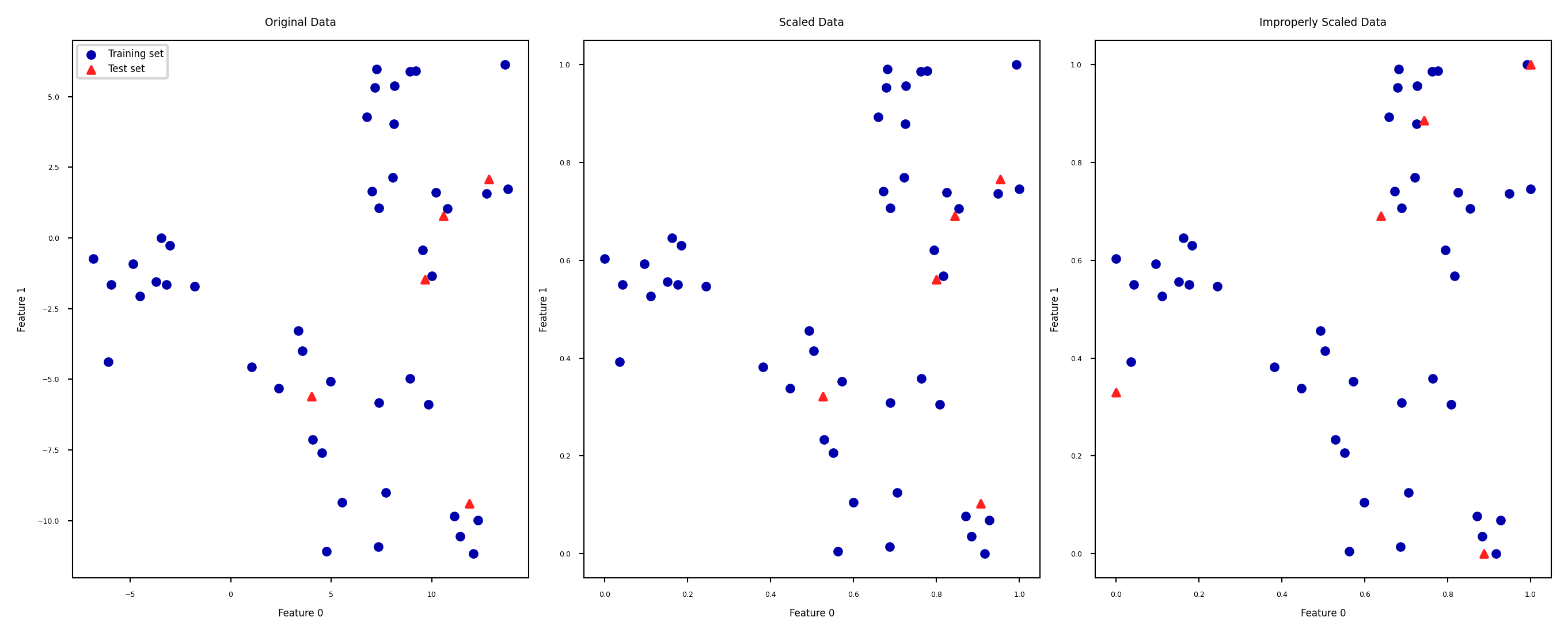
Test set distortion#
Properly scaled:
fiton training set,transformon training and test setImproperly scaled:
fitandtransformon the training and test data separatelyTest data points nowhere near same training data points
Show code cell source
from matplotlib.axes._axes import _log as matplotlib_axes_logger
matplotlib_axes_logger.setLevel('ERROR')
from sklearn.datasets import make_blobs
# make synthetic data
X, _ = make_blobs(n_samples=50, centers=5, random_state=4, cluster_std=2)
# split it into training and test set
X_train, X_test = train_test_split(X, random_state=5, test_size=.1)
# plot the training and test set
fig, axes = plt.subplots(1, 3, figsize=(10*fig_scale, 4*fig_scale))
axes[0].scatter(X_train[:, 0], X_train[:, 1],
c=mglearn.cm2(0), label="Training set", s=10*fig_scale)
axes[0].scatter(X_test[:, 0], X_test[:, 1], marker='^',
c=mglearn.cm2(1), label="Test set", s=10*fig_scale)
axes[0].legend(loc='upper left')
axes[0].set_title("Original Data")
# scale the data using MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# visualize the properly scaled data
axes[1].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
c=mglearn.cm2(0), label="Training set", s=10*fig_scale)
axes[1].scatter(X_test_scaled[:, 0], X_test_scaled[:, 1], marker='^',
c=mglearn.cm2(1), label="Test set", s=10*fig_scale)
axes[1].set_title("Scaled Data")
# rescale the test set separately
# so that test set min is 0 and test set max is 1
# DO NOT DO THIS! For illustration purposes only
test_scaler = MinMaxScaler()
test_scaler.fit(X_test)
X_test_scaled_badly = test_scaler.transform(X_test)
# visualize wrongly scaled data
axes[2].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
c=mglearn.cm2(0), label="training set", s=10*fig_scale)
axes[2].scatter(X_test_scaled_badly[:, 0], X_test_scaled_badly[:, 1],
marker='^', c=mglearn.cm2(1), label="test set", s=10*fig_scale)
axes[2].set_title("Improperly Scaled Data")
for ax in axes:
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
fig.tight_layout()
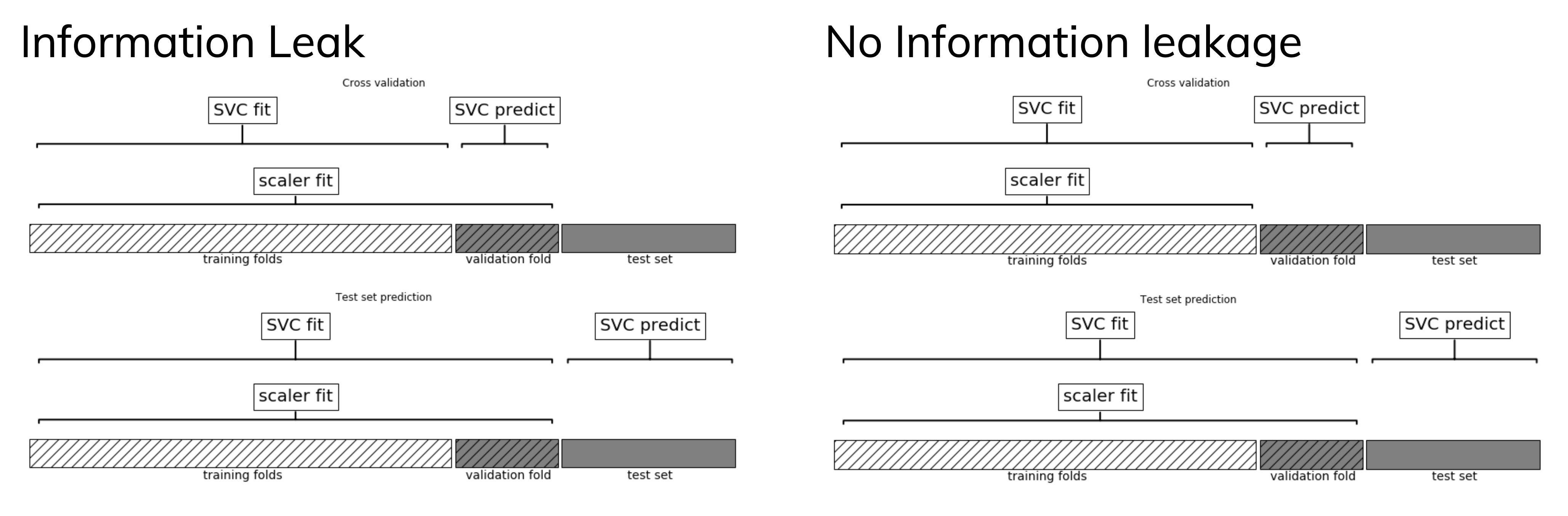
Data leakage#
Cross-validation: training set is split into training and validation sets for model selection
Incorrect: Scaler is fit on whole training set before doing cross-validation
Data leaks from validation folds into training folds, selected model may be optimistic
Right: Scaler is fit on training folds only
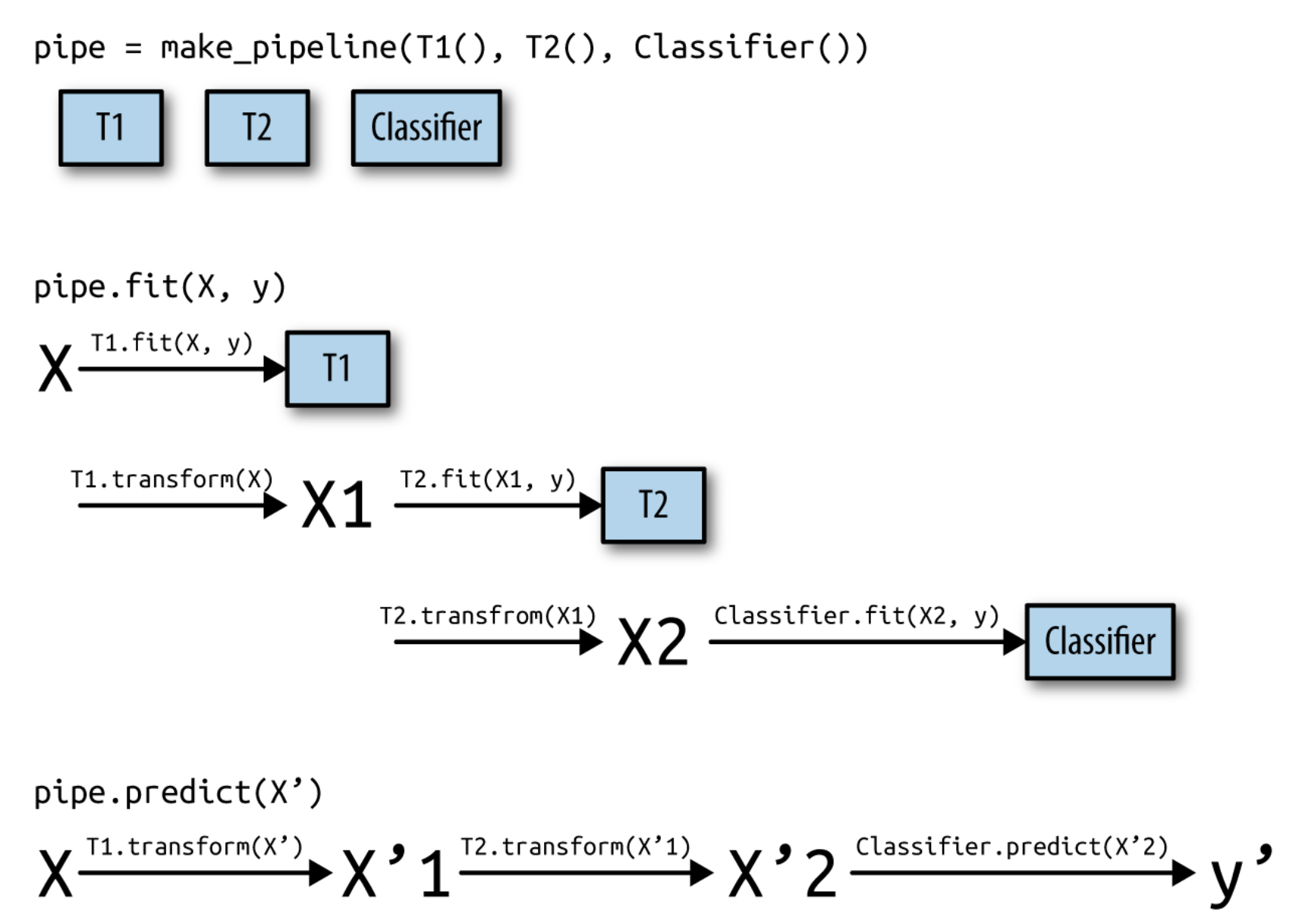
Pipelines#
A pipeline is a combination of data transformation and learning algorithms
It has a
fit,predict, andscoremethod, just like any other learning algorithmEnsures that data transformations are applied correctly
In practice (scikit-learn)#
A
pipelinecombines multiple processing steps in a single estimatorAll but the last step should be data transformer (have a
transformmethod)
# Make pipeline, step names will be 'minmaxscaler' and 'linearsvc'
pipe = make_pipeline(MinMaxScaler(), LinearSVC())
# Build pipeline with named steps
pipe = Pipeline([("scaler", MinMaxScaler()), ("svm", LinearSVC())])
# Correct fit and score
score = pipe.fit(X_train, y_train).score(X_test, y_test)
# Retrieve trained model by name
svm = pipe.named_steps["svm"]
# Correct cross-validation
scores = cross_val_score(pipe, X, y)
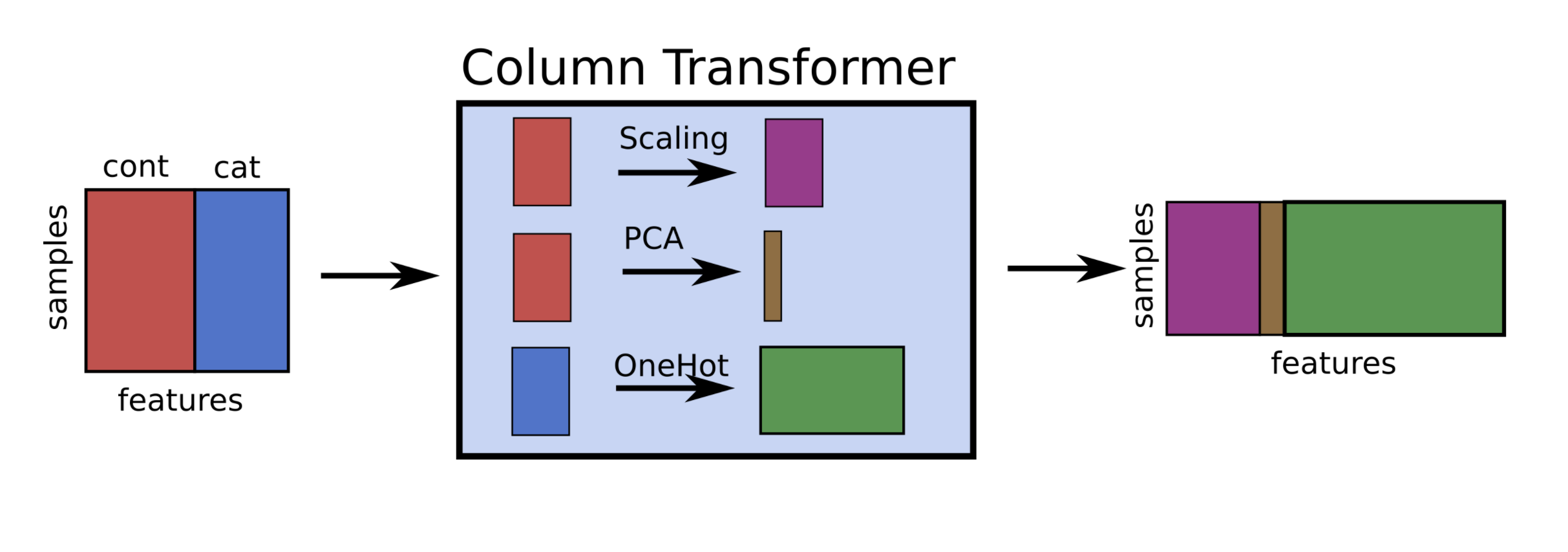
If you want to apply different preprocessors to different columns, use
ColumnTransformerIf you want to merge pipelines, you can use
FeatureUnionto concatenate columns
# 2 sub-pipelines, one for numeric features, other for categorical ones
numeric_pipe = make_pipeline(SimpleImputer(),StandardScaler())
categorical_pipe = make_pipeline(SimpleImputer(),OneHotEncoder())
# Using categorical pipe for features A,B,C, numeric pipe otherwise
preprocessor = make_column_transformer((categorical_pipe,
["A","B","C"]),
remainder=numeric_pipe)
# Combine with learning algorithm in another pipeline
``` python
pipe = make_pipeline(preprocessor, LinearSVC())
# Feature union of PCA features and selected features
union = FeatureUnion([("pca", PCA()), ("selected", SelectKBest())])
pipe = make_pipeline(union, LinearSVC())
ColumnTransformerconcatenates features in order
pipe = make_column_transformer((StandardScaler(),numeric_features),
(PCA(),numeric_features),
(OneHotEncoder(),categorical_features))
Pipeline selection#
We can safely use pipelines in model selection (e.g. grid search)
Use
'__'to refer to the hyperparameters of a step, e.g.svm__C
# Correct grid search (can have hyperparameters of any step)
param_grid = {'svm__C': [0.001, 0.01],
'svm__gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
grid = GridSearchCV(pipe, param_grid=param_grid).fit(X,y)
# Best estimator is now the best pipeline
best_pipe = grid.best_estimator_
# Tune pipeline and evaluate on held-out test set
grid = GridSearchCV(pipe, param_grid=param_grid).fit(X_train,y_train)
grid.score(X_test,y_test)
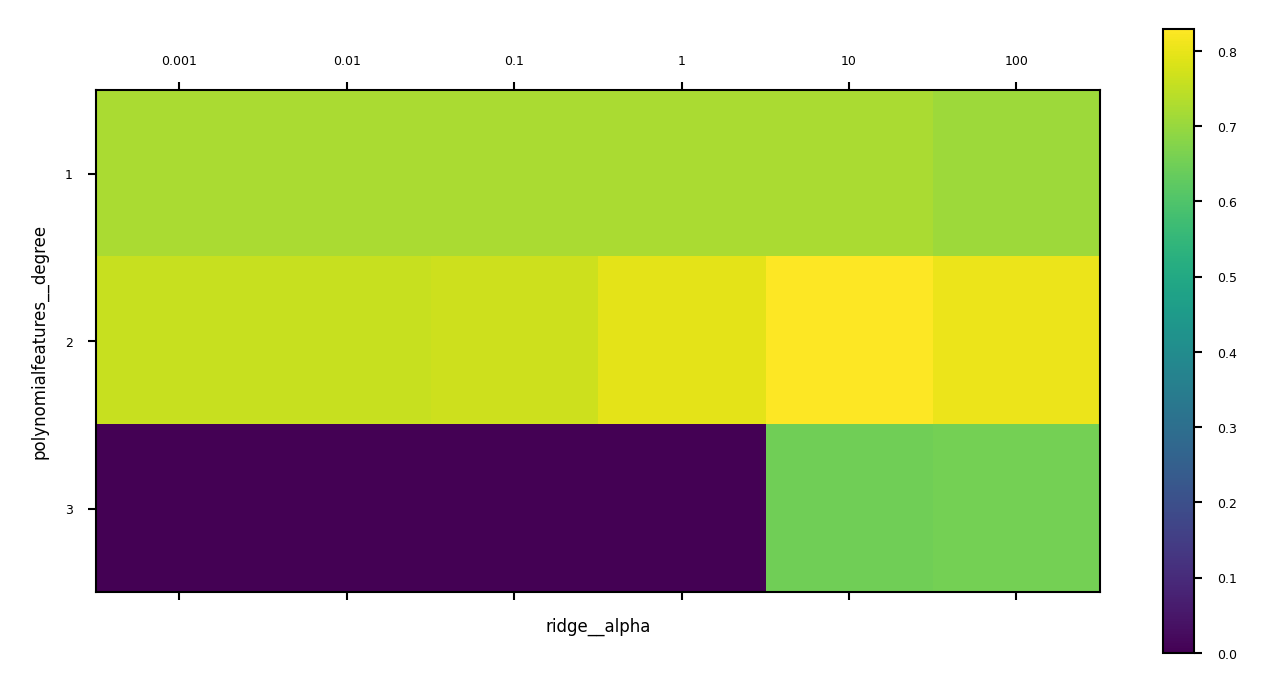
Example: Tune multiple steps at once#
pipe = make_pipeline(StandardScaler(),PolynomialFeatures(), Ridge())
param_grid = {'polynomialfeatures__degree': [1, 2, 3],
'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]}
grid = GridSearchCV(pipe, param_grid=param_grid).fit(X_train, y_train)
Show code cell source
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import fetch_openml
boston = fetch_openml(name="boston", as_frame=True)
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target,
random_state=0)
from sklearn.preprocessing import PolynomialFeatures
pipe = make_pipeline(StandardScaler(),PolynomialFeatures(),Ridge())
param_grid = {'polynomialfeatures__degree': [1, 2, 3],
'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]}
grid = GridSearchCV(pipe, param_grid=param_grid, cv=5)
grid.fit(X_train, y_train);
#plot
fig, ax = plt.subplots(figsize=(6*fig_scale, 3*fig_scale))
im = ax.matshow(grid.cv_results_['mean_test_score'].reshape(3, -1),
vmin=0, cmap="viridis")
ax.set_xlabel("ridge__alpha")
ax.set_ylabel("polynomialfeatures__degree")
ax.set_xticks(range(len(param_grid['ridge__alpha'])))
ax.set_xticklabels(param_grid['ridge__alpha'])
ax.set_yticks(range(len(param_grid['polynomialfeatures__degree'])))
ax.set_yticklabels(param_grid['polynomialfeatures__degree'])
plt.colorbar(im);
Automatic Feature Selection#
It can be a good idea to reduce the number of features to only the most useful ones
Simpler models that generalize better (less overfitting)
Curse of dimensionality (e.g. kNN)
Even models such as RandomForest can benefit from this
Sometimes it is one of the main methods to improve models (e.g. gene expression data)
Faster prediction and training
Training time can be quadratic (or cubic) in number of features
Easier data collection, smaller models (less storage)
More interpretable models: fewer features to look at
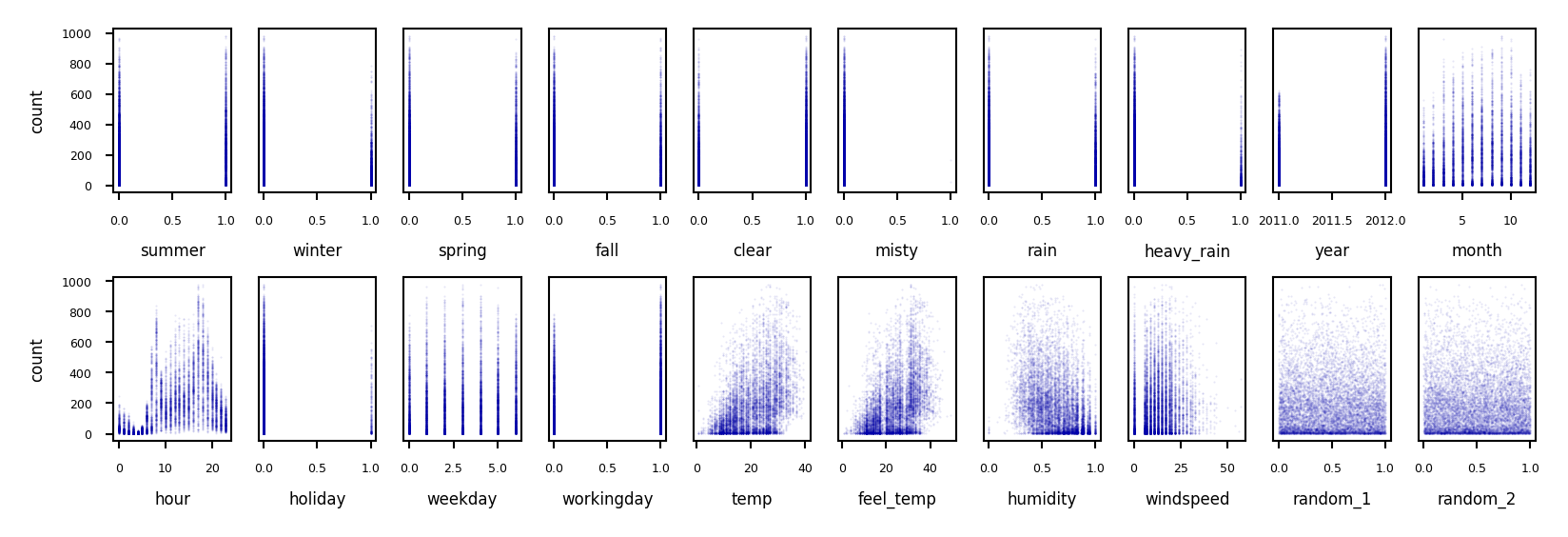
Example: bike sharing#
The Bike Sharing Demand dataset shows the amount of bikes rented in Washington DC
Some features are clearly more informative than others (e.g. temp, hour)
Some are correlated (e.g. temp and feel_temp)
We add two random features at the end
Show code cell source
from sklearn.datasets import fetch_openml
from sklearn.preprocessing import OneHotEncoder
# Get bike sharing data from OpenML
bikes = fetch_openml(data_id=42713, as_frame=True)
X_bike_cat, y_bike = bikes.data, bikes.target
# Optional: take half of the data to speed up processing
X_bike_cat = X_bike_cat.sample(frac=0.5, random_state=1)
y_bike = y_bike.sample(frac=0.5, random_state=1)
# One-hot encode the categorical features
encoder = OneHotEncoder(dtype=int)
preprocessor = ColumnTransformer(transformers=[('cat', encoder, [0,7])], remainder='passthrough')
X_bike = preprocessor.fit_transform(X_bike_cat,y)
# Add 2 random features at the end
random_features = np.random.rand(len(X_bike),2)
X_bike = np.append(X_bike,random_features, axis=1)
# Create feature names
bike_names = ['summer','winter', 'spring', 'fall', 'clear', 'misty', 'rain', 'heavy_rain']
bike_names.extend(X_bike_cat.columns[1:7])
bike_names.extend(X_bike_cat.columns[8:])
bike_names.extend(['random_1','random_2'])
Show code cell source
#pd.set_option('display.max_columns', 20)
#pd.DataFrame(data=X_bike, columns=bike_names).head()
Show code cell source
fig, axes = plt.subplots(2, 10, figsize=(6*fig_scale, 2*fig_scale))
for i, ax in enumerate(axes.ravel()):
ax.plot(X_bike[:, i], y_bike[:], '.', alpha=.1)
ax.set_xlabel("{}".format(bike_names[i]))
ax.get_yaxis().set_visible(False)
for i in range(2):
axes[i][0].get_yaxis().set_visible(True)
axes[i][0].set_ylabel("count")
fig.tight_layout()
Show code cell source
#fig, ax = plt.subplots(figsize=(6*fig_scale, 2*fig_scale))
#ax.plot(X_bike[:, 2])
#ax.plot(X_bike[:, 14])
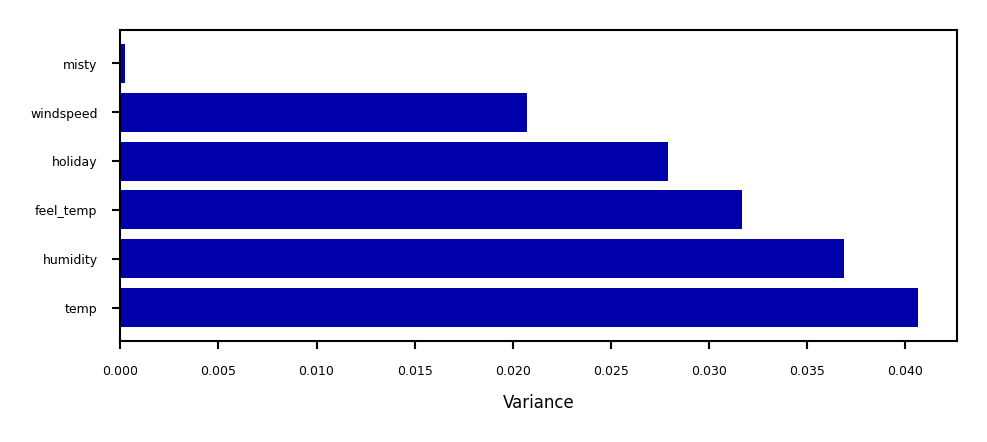
Unsupervised feature selection#
Variance-based
Remove (near) constant feature: choose a small variance threshold
Scale features before computing variance!
Infrequent values may still be important
Covariance-based
Remove correlated features
The small differences may actually be important
You don’t know because you don’t consider the target
Show code cell source
from sklearn.feature_selection import VarianceThreshold
selector = VarianceThreshold().fit(MinMaxScaler().fit_transform(X_bike))
variances = selector.variances_
var_sort = np.argsort(variances)
plt.figure(figsize=(4*fig_scale, 1.5*fig_scale))
ypos = np.arange(6)[::-1]
plt.barh(ypos, variances[var_sort][:6], align='center')
plt.yticks(ypos, np.array(bike_names)[var_sort][:6])
plt.xlabel("Variance");
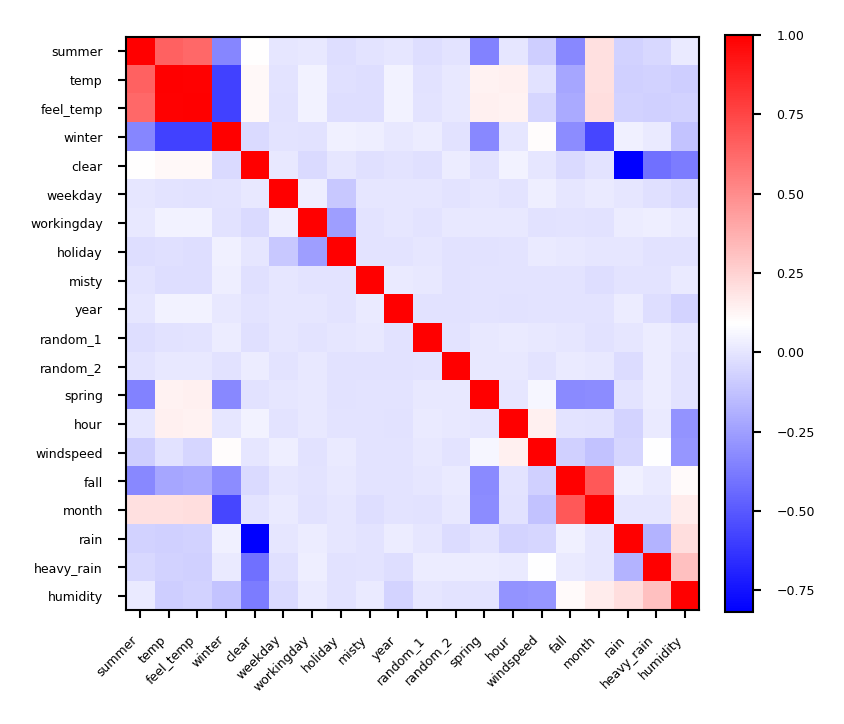
Covariance based feature selection#
Remove features \(X_i\) (= \(\mathbf{X_{:,i}}\)) that are highly correlated (have high correlation coefficient \(\rho\)) $\(\rho (X_1,X_2)={\frac {{\mathrm {cov}}(X_1,X_2)}{\sigma (X_1)\sigma (X_2)}} = {\frac { \frac{1}{N-1} \sum_i (X_{i,1} - \overline{X_1})(X_{i,2} - \overline{X_2}) }{\sigma (X_1)\sigma (X_2)}}\)$
Should we remove
feel_temp? Ortemp? Maybe one correlates more with the target?
Show code cell source
from sklearn.preprocessing import scale
from scipy.cluster import hierarchy
X_bike_scaled = scale(X_bike)
cov = np.cov(X_bike_scaled, rowvar=False)
order = np.array(hierarchy.dendrogram(hierarchy.ward(cov), no_plot=True)['ivl'], dtype="int")
bike_names_ordered = [bike_names[i] for i in order]
plt.figure(figsize=(3*fig_scale, 3*fig_scale))
plt.imshow(cov[order, :][:, order], cmap='bwr')
plt.xticks(range(X_bike.shape[1]), bike_names_ordered, ha="right")
plt.yticks(range(X_bike.shape[1]), bike_names_ordered)
plt.xticks(rotation=45)
plt.colorbar(fraction=0.046, pad=0.04);
Show code cell source
from sklearn.feature_selection import f_regression, SelectPercentile, mutual_info_regression, SelectFromModel, RFE
from sklearn.linear_model import RidgeCV, LassoCV
from sklearn.model_selection import cross_val_score, GridSearchCV
from sklearn.ensemble import RandomForestRegressor
from mlxtend.feature_selection import SequentialFeatureSelector
from sklearn.inspection import permutation_importance
from tqdm.notebook import trange, tqdm
# Pre-compute all importances on bike sharing dataset
# Scaled feature selection thresholds
thresholds = [0.25, 0.5, 0.75, 1]
# Dict to store all data
fs = {}
methods = ['FTest','MutualInformation','RandomForest','Ridge','Lasso','RFE',
'ForwardSelection','FloatingForwardSelection','Permutation']
for m in methods:
fs[m] = {}
fs[m]['select'] = {}
fs[m]['cv_score'] = {}
def cv_score(selector):
model = RandomForestRegressor() #RidgeCV() #RandomForestRegressor(n_estimators=100)
select_pipe = make_pipeline(StandardScaler(), selector, model)
return np.mean(cross_val_score(select_pipe, X_bike, y_bike, cv=3))
# Tuned RF (pre-computed to save time)
# param_grid = {"max_features":[2,4,8,16],"max_depth":[8,16,32,64,128]}
# randomforestCV = GridSearchCV(RandomForestRegressor(n_estimators=200),
# param_grid=param_grid).fit(X_bike, y_bike).best_estimator_
randomforestCV = RandomForestRegressor(n_estimators=200,max_features=16,max_depth=128)
# F test
print("Computing F test")
fs['FTest']['label'] = "F test"
fs['FTest']['score'] = f_regression(scale(X_bike),y_bike)[0]
fs['FTest']['scaled_score'] = fs['FTest']['score'] / np.max(fs['FTest']['score'])
for t in tqdm(thresholds):
selector = SelectPercentile(score_func=f_regression, percentile=t*100).fit(scale(X_bike), y_bike)
fs['FTest']['select'][t] = selector.get_support()
fs['FTest']['cv_score'][t] = cv_score(selector)
# Mutual information
print("Computing Mutual information")
fs['MutualInformation']['label'] = "Mutual Information"
fs['MutualInformation']['score'] = mutual_info_regression(scale(X_bike),y_bike,discrete_features=range(13)) # first 13 features are discrete
fs['MutualInformation']['scaled_score'] = fs['MutualInformation']['score'] / np.max(fs['MutualInformation']['score'])
for t in tqdm(thresholds):
selector = SelectPercentile(score_func=mutual_info_regression, percentile=t*100).fit(scale(X_bike), y_bike)
fs['MutualInformation']['select'][t] = selector.get_support()
fs['MutualInformation']['cv_score'][t] = cv_score(selector)
# Random Forest
print("Computing Random Forest")
fs['RandomForest']['label'] = "Random Forest"
fs['RandomForest']['score'] = randomforestCV.fit(X_bike, y_bike).feature_importances_
fs['RandomForest']['scaled_score'] = fs['RandomForest']['score'] / np.max(fs['RandomForest']['score'])
for t in tqdm(thresholds):
selector = SelectFromModel(randomforestCV, threshold="{}*mean".format((1-t))).fit(X_bike, y_bike) # Threshold can't be easily scaled here
fs['RandomForest']['select'][t] = selector.get_support()
fs['RandomForest']['cv_score'][t] = cv_score(selector)
# Ridge, Lasso
for m in [RidgeCV(),LassoCV()]:
name = m.__class__.__name__.replace('CV','')
print("Computing", name)
fs[name]['label'] = name
fs[name]['score'] = m.fit(X_bike, y_bike).coef_
fs[name]['scaled_score'] = np.abs(fs[name]['score']) / np.max(np.abs(fs[name]['score'])) # Use absolute values
for t in tqdm(thresholds):
selector = SelectFromModel(m, threshold="{}*mean".format((1-t)*2)).fit(scale(X_bike), y_bike)
fs[name]['select'][t] = selector.get_support()
fs[name]['cv_score'][t] = cv_score(selector)
# Recursive Feature Elimination
print("Computing RFE")
fs['RFE']['label'] = "Recursive Feature Elimination (with RandomForest)"
fs['RFE']['score'] = RFE(RandomForestRegressor(), n_features_to_select=1).fit(X_bike, y_bike).ranking_
fs['RFE']['scaled_score'] = (20 - fs['RFE']['score'])/ 19
for t in tqdm(thresholds):
selector = RFE(RandomForestRegressor(), n_features_to_select=int(t*20)).fit(X_bike, y_bike)
fs['RFE']['select'][t] = selector.support_
fs['RFE']['cv_score'][t] = cv_score(selector)
# Sequential Feature Selection
print("Computing Forward selection")
for floating in [False]: # Doing only non-floating to speed up computations
name = "{}ForwardSelection".format("Floating" if floating else "")
fs[name]['label'] = "{} (with Ridge)".format(name)
fs[name]['scaled_score'] = np.ones(20) # There is no scoring here
for t in tqdm(thresholds):
selector = SequentialFeatureSelector(RidgeCV(), k_features=int(t*20), forward=True, floating=floating).fit(X_bike, y_bike)
fs[name]['select'][t] = np.array([x in selector.k_feature_idx_ for x in range(20)])
fs[name]['cv_score'][t] = cv_score(selector)
# Permutation Importance
print("Computing Permutation importance")
fs['Permutation']['label'] = "Permutation importance (with RandomForest))"
fs['Permutation']['score'] = permutation_importance(RandomForestRegressor().fit(X_bike, y_bike), X_bike, y_bike,
n_repeats=10, random_state=42, n_jobs=-1).importances_mean
fs['Permutation']['scaled_score'] = fs['Permutation']['score'] / np.max(fs['Permutation']['score'])
sorted_idx = (-fs['Permutation']['score']).argsort() # inverted sort
for t in tqdm(thresholds):
mask = np.array([x in sorted_idx[:int(t*20)] for x in range(20)])
fs['Permutation']['select'][t] = mask
# Hard to use this in a pipeline, resorting to transforming the data beforehand
fs['Permutation']['cv_score'][t] = np.mean(cross_val_score(RandomForestRegressor(), X_bike[:,mask], y_bike, cv=3))
Computing F test
Computing Mutual information
Computing Random Forest
Computing Ridge
Computing Lasso
Computing RFE
Computing Forward selection
Computing Permutation importance
Show code cell source
def plot_feature_importances(method1='f_test', method2=None, threshold=0.5):
# Plot scores
x = np.arange(20)
fig, ax1 = plt.subplots(1, 1, figsize=(4*fig_scale, 1*fig_scale))
w = 0.3
imp = fs[method1]
mask = imp['select'][threshold]
m1 = ax1.bar(x[mask], imp['scaled_score'][mask], width=w, color='b', align='center')
ax1.bar(x[~mask], imp['scaled_score'][~mask], width=w, color='b', align='center', alpha=0.3)
if method2:
imp2 = fs[method2]
mask2 = imp2['select'][threshold]
ax2 = ax1.twinx()
m2 = ax2.bar(x[mask2] + w, imp2['scaled_score'][mask2], width=w,color='g',align='center')
ax2.bar(x[~mask2] + w, imp2['scaled_score'][~mask2], width=w,color='g',align='center', alpha=0.3)
plt.legend([m1, m2],['{} (Ridge R2:{:.2f})'.format(imp['label'],imp['cv_score'][threshold]),
'{} (Ridge R2:{:.2f})'.format(imp2['label'],imp2['cv_score'][threshold])], loc='upper left')
else:
plt.legend([m1],['{} (Ridge R2:{:.2f})'.format(imp['label'],imp['cv_score'][threshold])], loc='upper left')
ax1.set_xticks(range(len(bike_names)))
ax1.set_xticklabels(bike_names, rotation=45, ha="right");
plt.title("Feature importance (selection threshold {:.2f})".format(threshold))
plt.show()
Supervised feature selection: overview#
Univariate: F-test and Mutual Information
Model-based: Random Forests, Linear models, kNN
Wrapping techniques (black-box search)
Permutation importance
Show code cell source
@interact
def compare_feature_importances(method1=methods, method2=methods, threshold=(0.25,1,0.25)):
plot_feature_importances(method1,method2,threshold)
Univariate statistics (F-test)#
Consider each feature individually (univariate), independent of the model that you aim to apply
Use a statistical test: is there a linear statistically significant relationship with the target?
Use F-statistic (or corresponding p value) to rank all features, then select features using a threshold
Best \(k\), best \(k\) %, probability of removing useful features (FPR),…
Cannot detect correlations (e.g. temp and feel_temp) or interactions (e.g. binary features)
Show code cell source
plot_feature_importances('FTest', None, threshold=0.75)
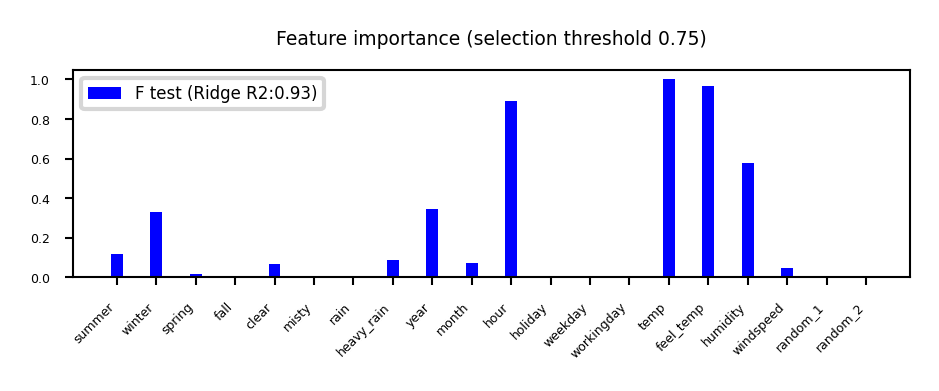
F-statistic#
For regression: does feature \(X_i\) correlate (positively or negatively) with the target \(y\)? $\(\text{F-statistic} = \frac{\rho(X_i,y)^2}{1-\rho(X_i,y)^2} \cdot (N-1)\)$
For classification: uses ANOVA: does \(X_i\) explain the between-class variance?
Alternatively, use the \(\chi^2\) test (only for categorical features) $\(\text{F-statistic} = \frac{\text{within-class variance}}{\text{between-class variance}} =\frac{var(\overline{X_i})}{\overline{var(X_i)}}\)$
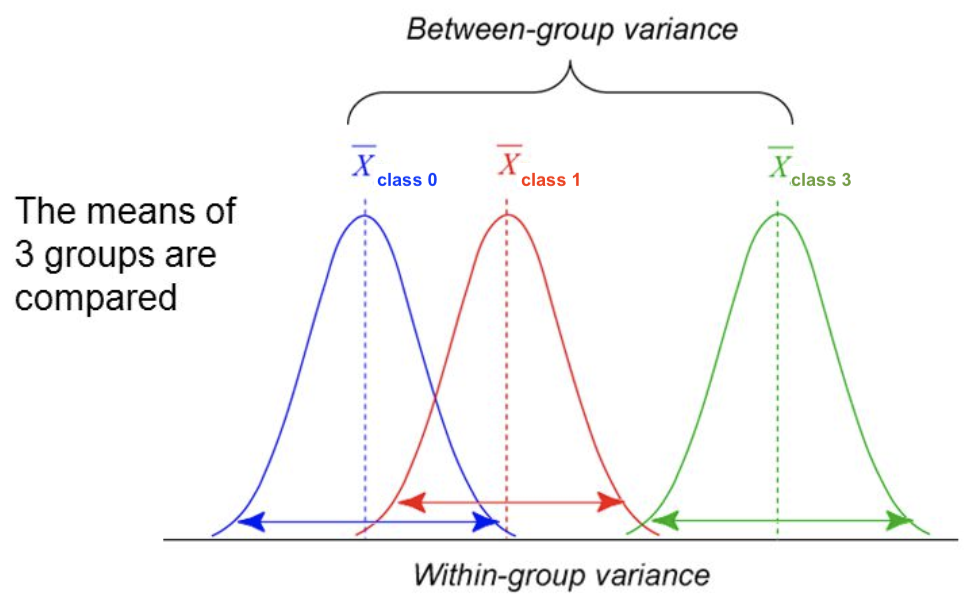
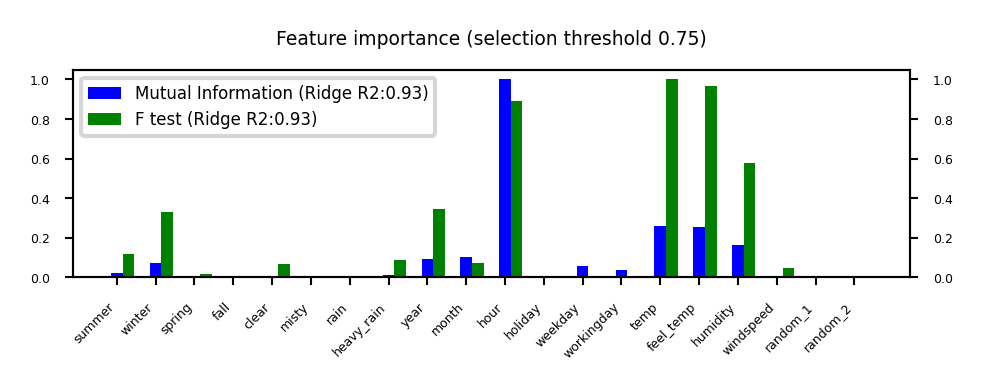
Mutual information#
Measures how much information \(X_i\) gives about the target \(Y\). In terms of entropy \(H\): $\(MI(X,Y) = H(X) + H(Y) - H(X,Y)\)$
Idea: estimate H(X) as the average distance between a data point and its \(k\) Nearest Neighbors
You need to choose \(k\) and say which features are categorical
Captures complex dependencies (e.g. hour, month), but requires more samples to be accurate
Show code cell source
plot_feature_importances('MutualInformation', 'FTest', threshold=0.75)
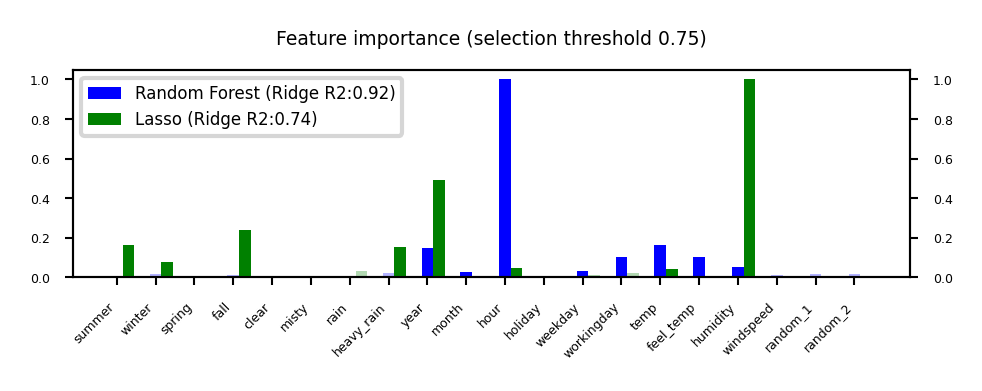
Model-based Feature Selection#
Use a tuned(!) supervised model to judge the importance of each feature
Linear models (Ridge, Lasso, LinearSVM,…): features with highest weights (coefficients)
Tree–based models: features used in first nodes (high information gain)
Selection model can be different from the one you use for final modelling
Captures interactions: features are more/less informative in combination (e.g. winter, temp)
RandomForests: learns complex interactions (e.g. hour), but biased to high cardinality features
Show code cell source
plot_feature_importances('RandomForest', 'Lasso', threshold=0.75)
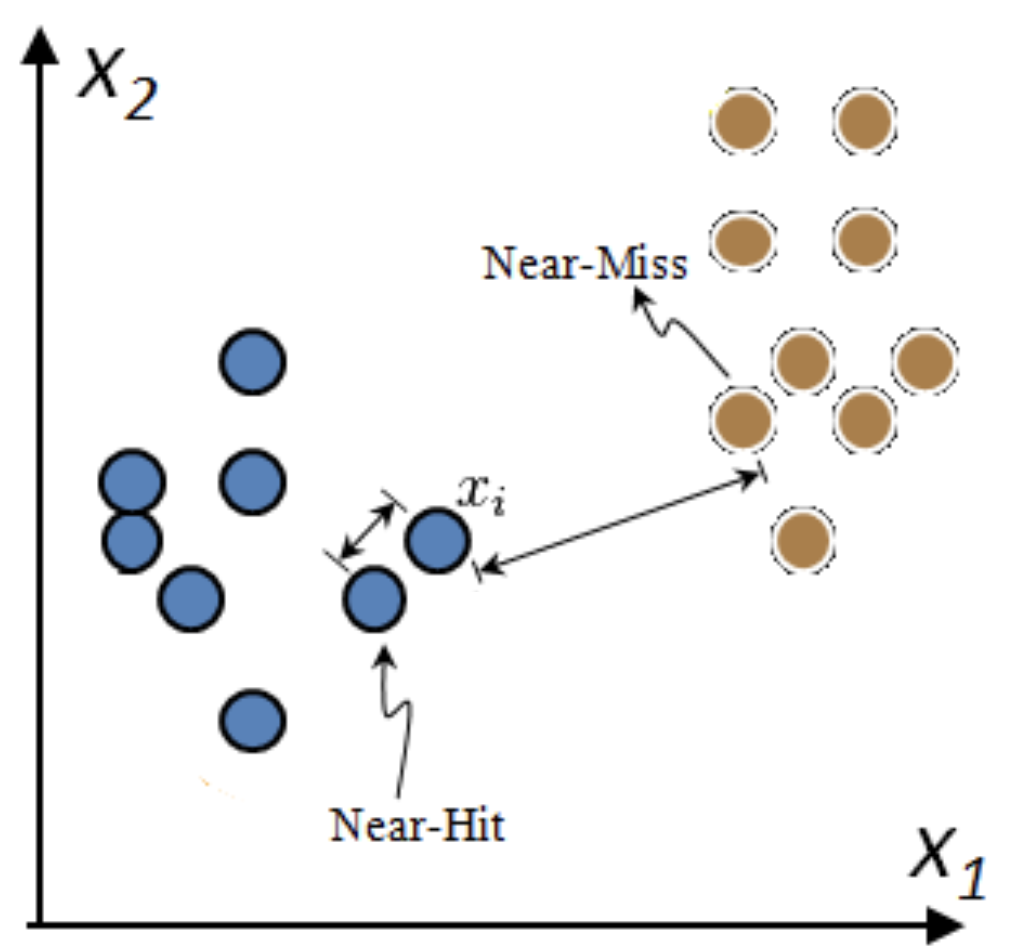
Relief: Model-based selection with kNN#
For I iterations, choose a random point \(\mathbf{x_i}\) and find \(k\) nearest neighbors \(\mathbf{x_{k}}\)
Increase feature weights if \(\mathbf{x_i}\) and \(\mathbf{x_{k}}\) have different class (near miss), else decrease
\(\mathbf{w_i} = \mathbf{w_{i-1}} + (\mathbf{x_i} - \text{nearMiss}_i)^2 - (\mathbf{x_i} - \text{nearHit}_i)^2\)
Many variants: ReliefF (uses L1 norm, faster), RReliefF (for regression), …
Iterative Model-based Feature Selection#
Dropping many features at once is not ideal: feature importance may change in subset
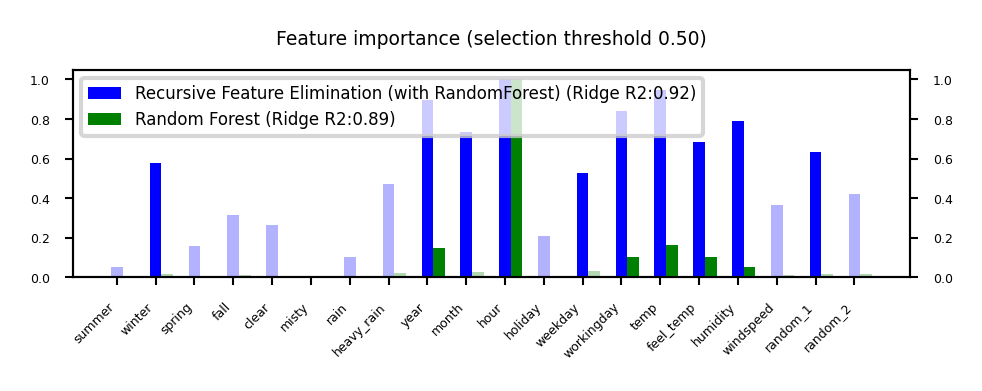
Recursive Feature Elimination (RFE)
Remove \(s\) least important feature(s), recompute remaining importances, repeat
Can be rather slow
Show code cell source
plot_feature_importances('RFE', 'RandomForest', threshold=0.5)
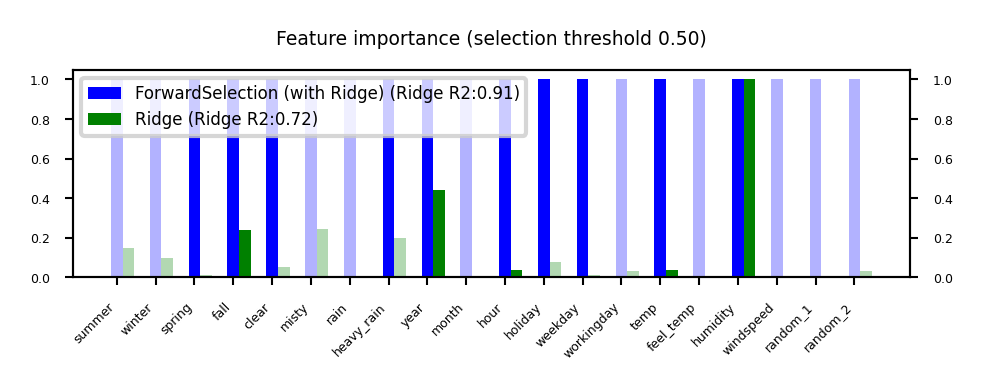
Sequential feature selection (Wrapping)#
Evaluate your model with different sets of features, find best subset based on performance
Greedy black-box search (can end up in local minima)
Backward selection: remove least important feature, recompute importances, repeat
Forward selection: set aside most important feature, recompute importances, repeat
Floating: add best new feature, remove worst one, repeat (forward or backward)
Stochastic search: use random mutations in candidate subset (e.g. simulated annealing)
Show code cell source
plot_feature_importances('ForwardSelection', 'Ridge', threshold=0.5)
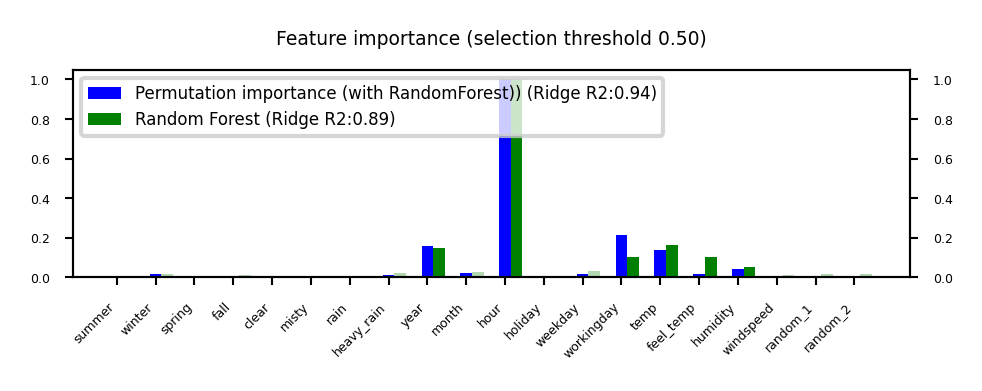
Permutation feature importance#
Defined as the decrease in model performance when a single feature value is randomly shuffled
This breaks the relationship between the feature and the target
Model agnostic, metric agnostic, and can be calculated many times with different permutations
Can be applied to unseen data (not possible with model-based techniques)
Less biased towards high-cardinality features (compared with RandomForests)
Show code cell source
plot_feature_importances('Permutation', 'RandomForest', threshold=0.5)
Comparison#
Feature importances (scaled) and cross-validated \(R^2\) score of pipeline
Pipeline contains features selection + Ridge
Selection threshold value ranges from 25% to 100% of all features
Best method ultimately depends on the problem and dataset at hand
Show code cell source
@interact
def compare_feature_importances(method1=methods, method2=methods, threshold=(0.25,1,0.25)):
plot_feature_importances(method1,method2,threshold)
Show code cell source
if not interactive:
plot_feature_importances('Permutation', 'FTest', threshold=0.5)
In practice (scikit-learn)#
Unsupervised:
VarianceTreshold
selector = VarianceThreshold(threshold=0.01)
X_selected = selector.fit_transform(X)
variances = selector.variances_
Univariate:
For regression:
f_regression,mutual_info_regressionFor classification:
f_classification,chi2,mutual_info_classicationSelecting:
SelectKBest,SelectPercentile,SelectFpr,…
selector = SelectPercentile(score_func=f_regression, percentile=50)
X_selected = selector.fit_transform(X,y)
selected_features = selector.get_support()
f_values, p_values = f_regression(X,y)
mi_values = mutual_info_regression(X,y,discrete_features=[])
Model-based:
SelectFromModel: requires a model and a selection thresholdRFE,RFECV(recursive feature elimination): requires model and final nr features
selector = SelectFromModel(RandomForestRegressor(), threshold='mean')
rfe_selector = RFE(RidgeCV(), n_features_to_select=20)
X_selected = selector.fit_transform(X)
rf_importances = Randomforest().fit(X, y).feature_importances_
Sequential feature selection (from
mlxtend, sklearn-compatible)
selector = SequentialFeatureSelector(RidgeCV(), k_features=20, forward=True,
floating=True)
X_selected = selector.fit_transform(X)
Permutation Importance (in
sklearn.inspection), no fit-transform interface
importances = permutation_importance(RandomForestRegressor().fit(X,y),
X, y, n_repeats=10).importances_mean
feature_ids = (-importances).argsort()[:n]
Feature Engineering#
Create new features based on existing ones
Polynomial features
Interaction features
Binning
Mainly useful for simple models (e.g. linear models)
Other models can learn interations themselves
But may be slower, less robust than linear models
Polynomials#
Add all polynomials up to degree \(d\) and all products
Equivalent to polynomial basis expansions $\([1, x_1, ..., x_p] \xrightarrow{} [1, x_1, ..., x_p, x_1^2, ..., x_p^2, ..., x_p^d, x_1 x_2, ..., x_{p-1} x_p]\)$
Show code cell source
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.preprocessing import PolynomialFeatures
# Wavy data
X, y = mglearn.datasets.make_wave(n_samples=100)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
# Normal ridge
lreg = Ridge().fit(X, y)
plt.rcParams['figure.figsize'] = [6*fig_scale, 4*fig_scale]
plt.plot(line, lreg.predict(line), lw=2, label="Ridge")
# include polynomials up to x ** 10
poly = PolynomialFeatures(degree=10, include_bias=False)
X_poly = poly.fit_transform(X)
preg = Ridge().fit(X_poly, y)
line_poly = poly.transform(line)
plt.plot(line, preg.predict(line_poly), lw=2, label='Ridge (polynomial)')
plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.legend(loc="best");
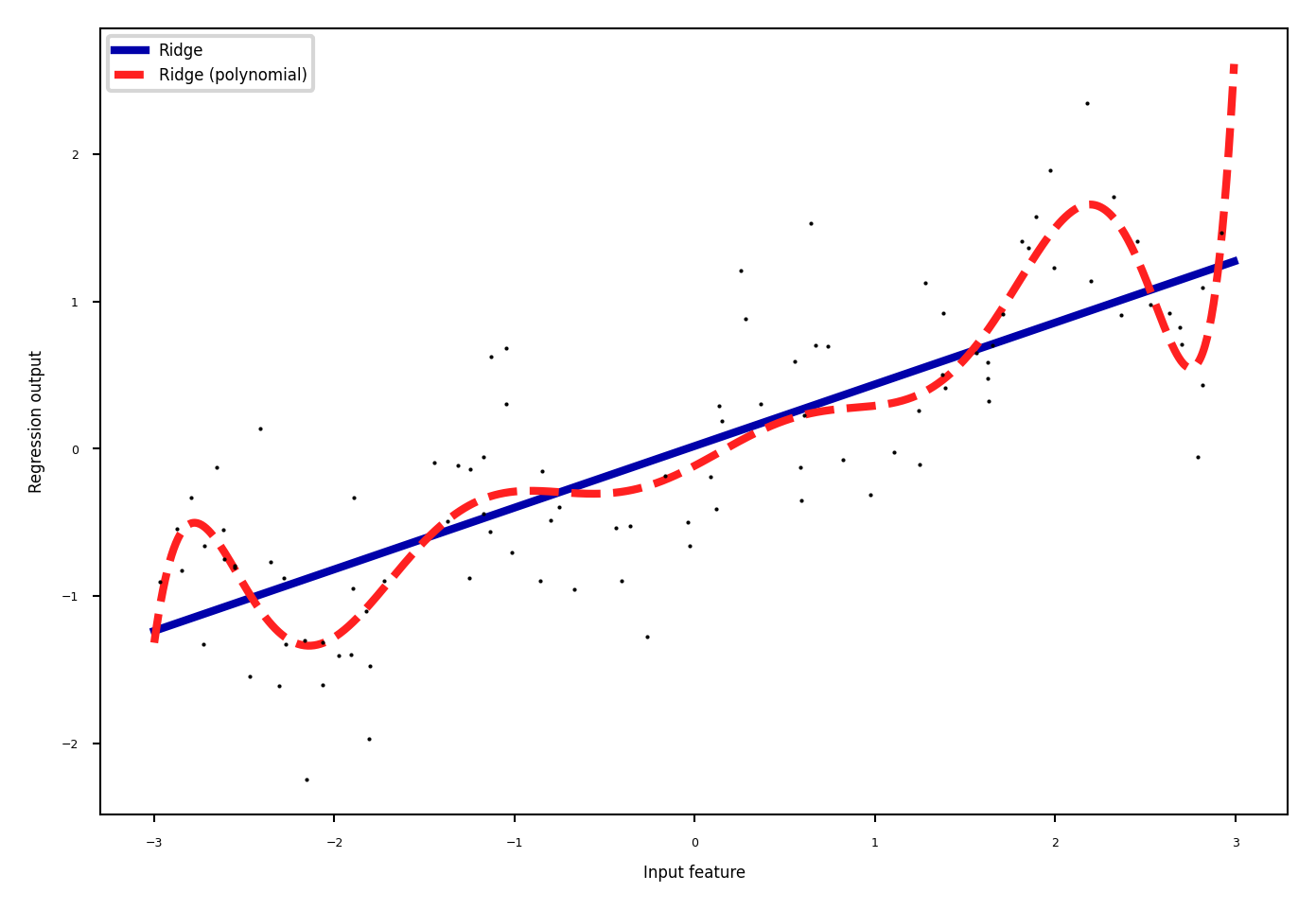
Binning#
Partition numeric feature values into \(n\) intervals (bins)
Create \(n\) new one-hot features, 1 if original value falls in corresponding bin
Models different intervals differently (e.g. different age groups)
Show code cell source
from sklearn.preprocessing import OneHotEncoder
# create 11 equal bins
bins = np.linspace(-3, 3, 5)
# assign to bins
which_bin = np.digitize(X, bins=bins)
# transform using the OneHotEncoder.
encoder = OneHotEncoder(sparse_output=False)
# encoder.fit finds the unique values that appear in which_bin
encoder.fit(which_bin)
# transform creates the one-hot encoding
X_binned = encoder.transform(which_bin)
# Plot transformed data
bin_names = [('[%.1f,%.1f]') % i for i in zip(bins, bins[1:])]
df_orig = pd.DataFrame(X, columns=["orig"])
df_nr = pd.DataFrame(which_bin, columns=["which_bin"])
# add the original features
X_combined = np.hstack([X, X_binned])
ohedf = pd.DataFrame(X_combined, columns=["orig"]+bin_names).head(3)
ohedf.style.set_table_styles(dfstyle)
| orig | [-3.0,-1.5] | [-1.5,0.0] | [0.0,1.5] | [1.5,3.0] | |
|---|---|---|---|---|---|
| 0 | -0.752759 | 0.000000 | 1.000000 | 0.000000 | 0.000000 |
| 1 | 2.704286 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| 2 | 1.391964 | 0.000000 | 0.000000 | 1.000000 | 0.000000 |
Show code cell source
line_binned = encoder.transform(np.digitize(line, bins=bins))
reg = LinearRegression().fit(X_combined, y)
line_combined = np.hstack([line, line_binned])
plt.rcParams['figure.figsize'] = [6*fig_scale, 3*fig_scale]
plt.plot(line, lreg.predict(line), lw=2, label="Ridge")
plt.plot(line, reg.predict(line_combined), lw=2, label='Ridge (binned)')
for bin in bins:
plt.plot([bin, bin], [-3, 3], ':', c='k')
plt.legend(loc="best")
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.plot(X[:, 0], y, 'o', c='k');
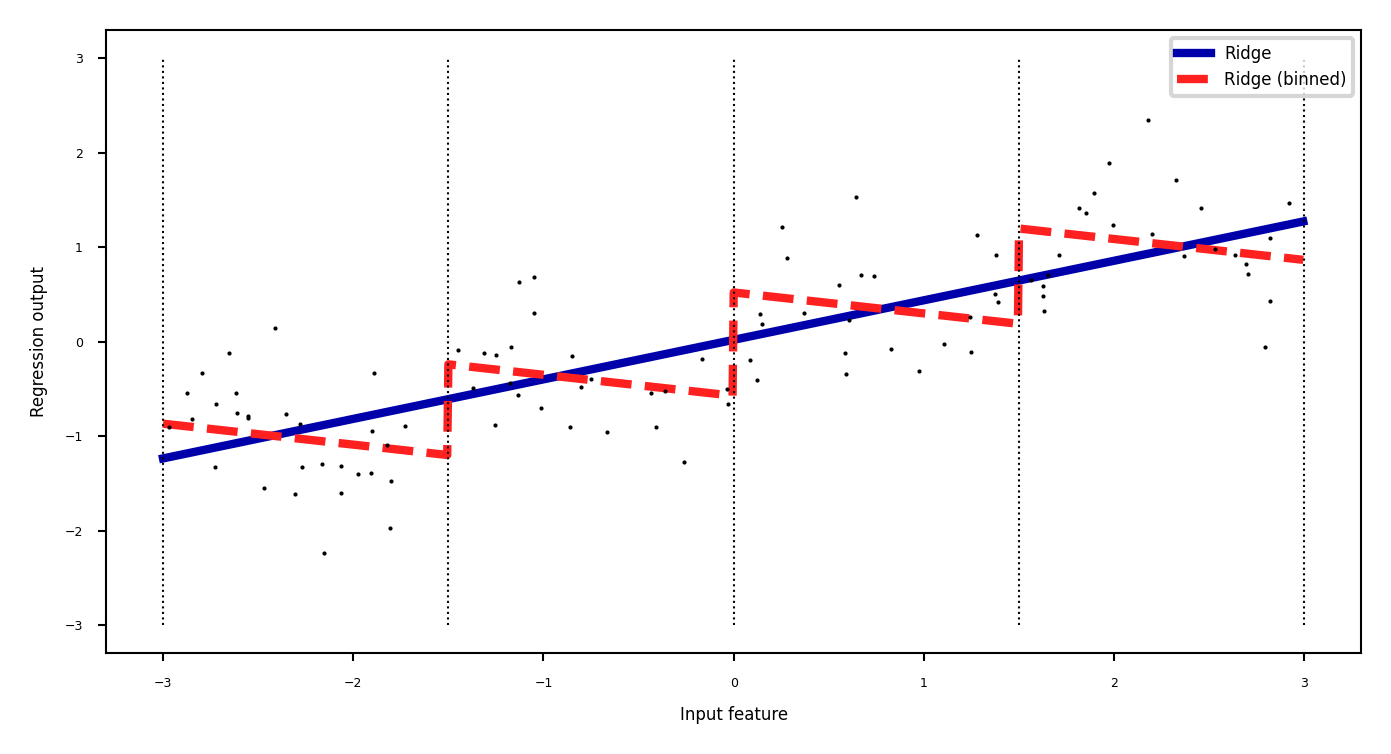
Binning + interaction features#
Add interaction features (or product features )
Product of the bin encoding and the original feature value
Learn different weights per bin
Show code cell source
X_product = np.hstack([X_binned, X * X_binned])
bin_sname = ["b" + str(s) for s in range(4)]
X_combined = np.hstack([X, X_product])
pd.set_option('display.max_columns', 10)
bindf = pd.DataFrame(X_combined, columns=["orig"]+bin_sname+["X*" + s for s in bin_sname]).head(3)
bindf.style.set_table_styles(dfstyle)
| orig | b0 | b1 | b2 | b3 | X*b0 | X*b1 | X*b2 | X*b3 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | -0.752759 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | -0.000000 | -0.752759 | -0.000000 | -0.000000 |
| 1 | 2.704286 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 2.704286 |
| 2 | 1.391964 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 1.391964 | 0.000000 |
Show code cell source
reg = LinearRegression().fit(X_product, y)
line_product = np.hstack([line_binned, line * line_binned])
plt.plot(line, lreg.predict(line), lw=2, label="Ridge")
plt.plot(line, reg.predict(line_product), lw=2, label='Ridge (binned+interactions)')
for bin in bins:
plt.plot([bin, bin], [-3, 3], ':', c='k')
plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.legend(loc="best");
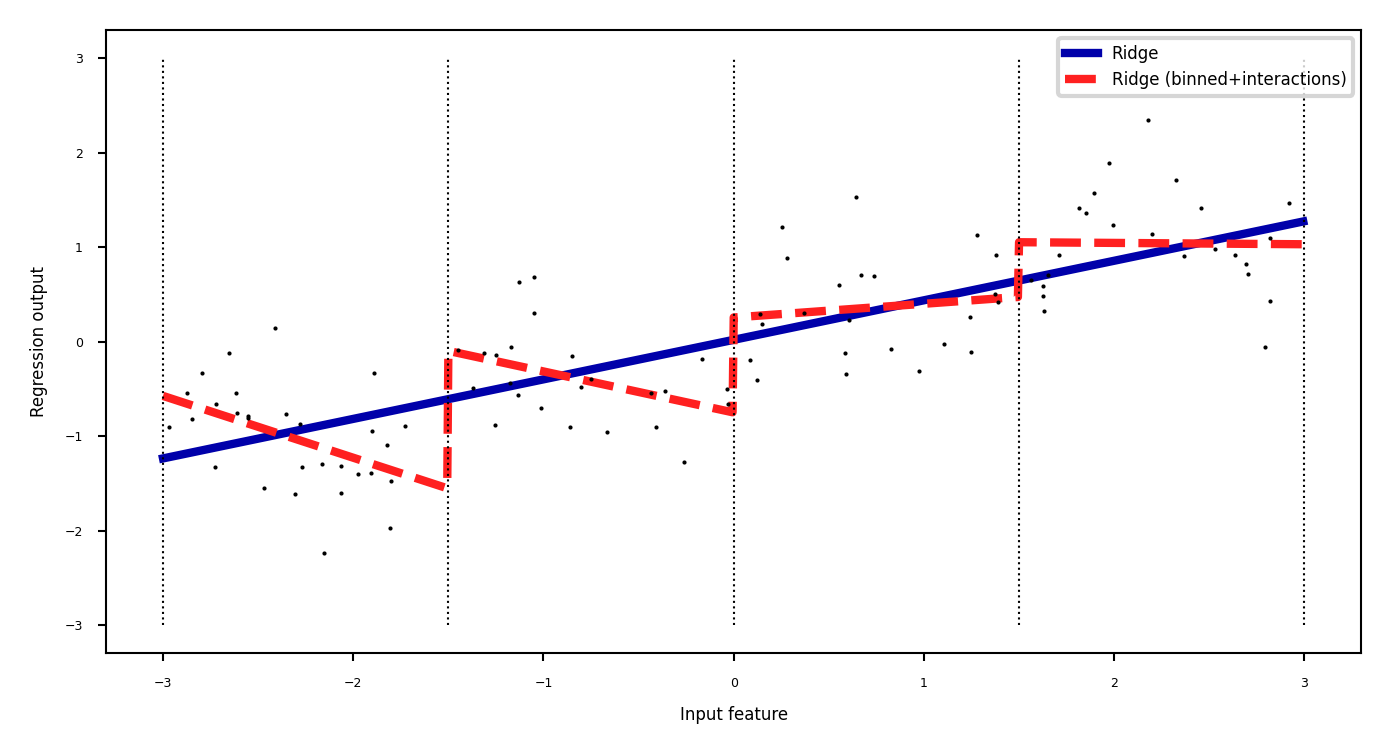
Categorical feature interactions#
One-hot-encode categorical feature
Multiply every one-hot-encoded column with every numeric feature
Allows to built different submodels for different categories
Show code cell source
df = pd.DataFrame({'gender': ['M', 'F', 'M', 'F', 'F'],
'age': [14, 16, 12, 25, 22],
'pageviews': [70, 12, 42, 64, 93],
'time': [269, 1522, 235, 63, 21]
})
df.head(3)
df.style.set_table_styles(dfstyle)
| gender | age | pageviews | time | |
|---|---|---|---|---|
| 0 | M | 14 | 70 | 269 |
| 1 | F | 16 | 12 | 1522 |
| 2 | M | 12 | 42 | 235 |
| 3 | F | 25 | 64 | 63 |
| 4 | F | 22 | 93 | 21 |
Show code cell source
dummies = pd.get_dummies(df)
df_f = dummies.multiply(dummies.gender_F, axis='rows')
df_f = df_f.rename(columns=lambda x: x + "_F")
df_m = dummies.multiply(dummies.gender_M, axis='rows')
df_m = df_m.rename(columns=lambda x: x + "_M")
res = pd.concat([df_m, df_f], axis=1).drop(["gender_F_M", "gender_M_F"], axis=1)
res.head(3)
res.style.set_table_styles(dfstyle)
| age_M | pageviews_M | time_M | gender_M_M | age_F | pageviews_F | time_F | gender_F_F | |
|---|---|---|---|---|---|---|---|---|
| 0 | 14 | 70 | 269 | True | 0 | 0 | 0 | False |
| 1 | 0 | 0 | 0 | False | 16 | 12 | 1522 | True |
| 2 | 12 | 42 | 235 | True | 0 | 0 | 0 | False |
| 3 | 0 | 0 | 0 | False | 25 | 64 | 63 | True |
| 4 | 0 | 0 | 0 | False | 22 | 93 | 21 | True |
Missing value imputation#
Data can be missing in different ways:
Missing Completely at Random (MCAR): purely random points are missing
Missing at Random (MAR): something affects missingness, but no relation with the value
E.g. faulty sensors, some people don’t fill out forms correctly
Missing Not At Random (MNAR): systematic missingness linked to the value
Has to be modelled or resolved (e.g. sensor decay, sick people leaving study)
Missingness can be encoded in different ways:’?’, ‘-1’, ‘unknown’, ‘NA’,…
Also labels can be missing (remove example or use semi-supervised learning)
Show code cell source
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import SimpleImputer, KNNImputer, IterativeImputer
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import BayesianRidge
from fancyimpute import SoftImpute, IterativeSVD, MatrixFactorization
from sklearn.utils._testing import ignore_warnings
from sklearn.exceptions import ConvergenceWarning
import matplotlib.lines as mlines
# Colors
norm = plt.Normalize()
colors = plt.cm.jet(norm([0,1,2]))
colors
# Iris dataset with some added noise and missing values
def missing_iris():
iris = fetch_openml("iris", version=1, return_X_y=True, as_frame=False)
X, y = iris
# Make some noise
np.random.seed(0)
noise = np.random.normal(0, 0.1, 150)
for i in range(4):
X[:, i] = X[:, i] + noise
# Add missing data. Set smallest leaf measurements to NaN
rng = np.random.RandomState(0)
mask = np.abs(X[:, 2] - rng.normal(loc=3.5, scale=.9, size=X.shape[0])) < 0.6
X[mask, 2] = np.NaN
mask2 = np.abs(X[:, 3] - rng.normal(loc=7.5, scale=.9, size=X.shape[0])) > 6.5
X[mask2, 3] = np.NaN
label_encoder = LabelEncoder().fit(y)
y = label_encoder.transform(y)
return X, y
# List of my favorite imputers
imputers = {"Mean Imputation": SimpleImputer(strategy="mean"),
"kNN Imputation": KNNImputer(),
"Iterative Imputation (RandomForest)": IterativeImputer(RandomForestRegressor()),
"Iterative Imputation (BayesianRidge)": IterativeImputer(BayesianRidge()),
"SoftImpute": SoftImpute(verbose=0),
"Matrix Factorization": MatrixFactorization(verbose=0)
}
@ignore_warnings(category=ConvergenceWarning)
@ignore_warnings(category=UserWarning)
def plot_imputation(imputer=imputers.keys()):
X, y = missing_iris()
imputed_mask = np.any(np.isnan(X), axis=1)
X_imp = None
scores = None
imp = imputers[imputer]
if isinstance(imp, SimpleImputer) or isinstance(imp, KNNImputer) or isinstance(imp, IterativeImputer):
X_imp = imp.fit_transform(X)
imp_pipe = make_pipeline(SimpleImputer(), imp, LogisticRegression())
scores = cross_val_score(imp_pipe, X_imp, y)
else:
X_imp = imp.fit_transform(X)
scores = cross_val_score(LogisticRegression(), X_imp, y)
fig, ax = plt.subplots(1, 1, figsize=(5*fig_scale, 3*fig_scale))
ax.set_title("{} (ACC:{:.3f})".format(imputer, np.mean(scores)))
ax.scatter(X_imp[imputed_mask, 2], X_imp[imputed_mask, 3], c=y[imputed_mask], cmap='brg', alpha=.3, marker="s", linewidths=0.25, s=4)
ax.scatter(X_imp[~imputed_mask, 2], X_imp[~imputed_mask, 3], c=y[~imputed_mask], cmap='brg', alpha=.6)
# this is for creating the legend...
square = plt.Line2D((0,), (0,), linestyle='', marker="s", markerfacecolor="w", markeredgecolor="k", markeredgewidth=0.5, label='Imputed data')
circle = plt.Line2D((0,), (0,), linestyle='', marker="o", markerfacecolor="w", markeredgecolor="k", markeredgewidth=0.5, label='Real data')
plt.legend(handles=[square, circle], numpoints=1, loc="best")
(CVXPY) Mar 06 01:10:33 AM: Encountered unexpected exception importing solver CVXOPT:
ImportError("dlopen(/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so, 0x0002): tried: '/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so' (mach-o file, but is an incompatible architecture (have 'x86_64', need 'arm64')), '/System/Volumes/Preboot/Cryptexes/OS/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so' (no such file), '/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so' (mach-o file, but is an incompatible architecture (have 'x86_64', need 'arm64'))")
(CVXPY) Mar 06 01:10:33 AM: Encountered unexpected exception importing solver GLPK:
ImportError("dlopen(/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so, 0x0002): tried: '/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so' (mach-o file, but is an incompatible architecture (have 'x86_64', need 'arm64')), '/System/Volumes/Preboot/Cryptexes/OS/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so' (no such file), '/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so' (mach-o file, but is an incompatible architecture (have 'x86_64', need 'arm64'))")
(CVXPY) Mar 06 01:10:33 AM: Encountered unexpected exception importing solver GLPK_MI:
ImportError("dlopen(/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so, 0x0002): tried: '/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so' (mach-o file, but is an incompatible architecture (have 'x86_64', need 'arm64')), '/System/Volumes/Preboot/Cryptexes/OS/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so' (no such file), '/Users/jvanscho/miniconda3/lib/python3.10/site-packages/cvxopt/base.cpython-310-darwin.so' (mach-o file, but is an incompatible architecture (have 'x86_64', need 'arm64'))")
Overview#
Mean/constant imputation
kNN-based imputation
Iterative (model-based) imputation
Matrix Factorization techniques
Show code cell source
from ipywidgets import interact, interact_manual
from sklearn.datasets import fetch_openml
from sklearn.preprocessing import LabelEncoder
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import cross_val_score
@interact
def compare_imputers(imputer=imputers.keys()):
plot_imputation(imputer=imputer)
Show code cell source
if not interactive:
plot_imputation("kNN Imputation")
Mean imputation#
Replace all missing values of a feature by the same value
Numerical features: mean or median
Categorical features: most frequent category
Constant value, e.g. 0 or ‘missing’ for text features
Optional: add an indicator column for missingness
Example: Iris dataset (randomly removed values in 3rd and 4th column)
Show code cell source
plot_imputation("Mean Imputation")
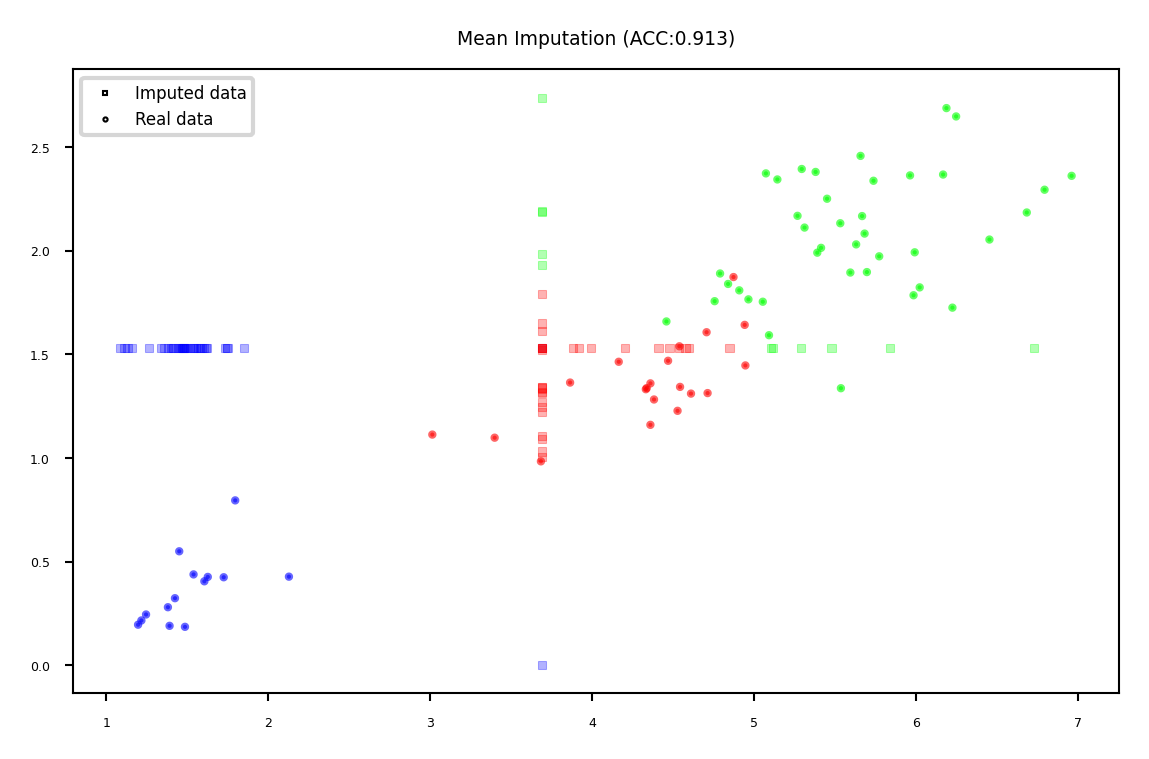
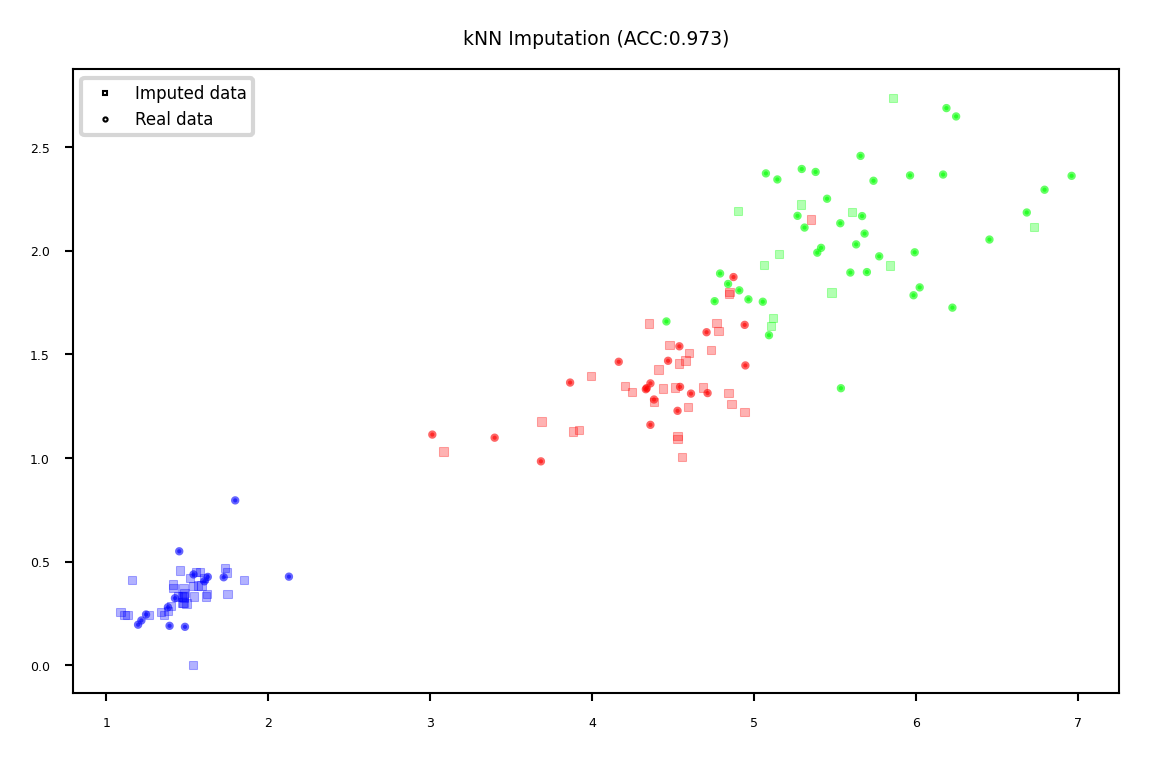
kNN imputation#
Use special version of kNN to predict value of missing points
Uses only non-missing data when computing distances
Show code cell source
plot_imputation("kNN Imputation")
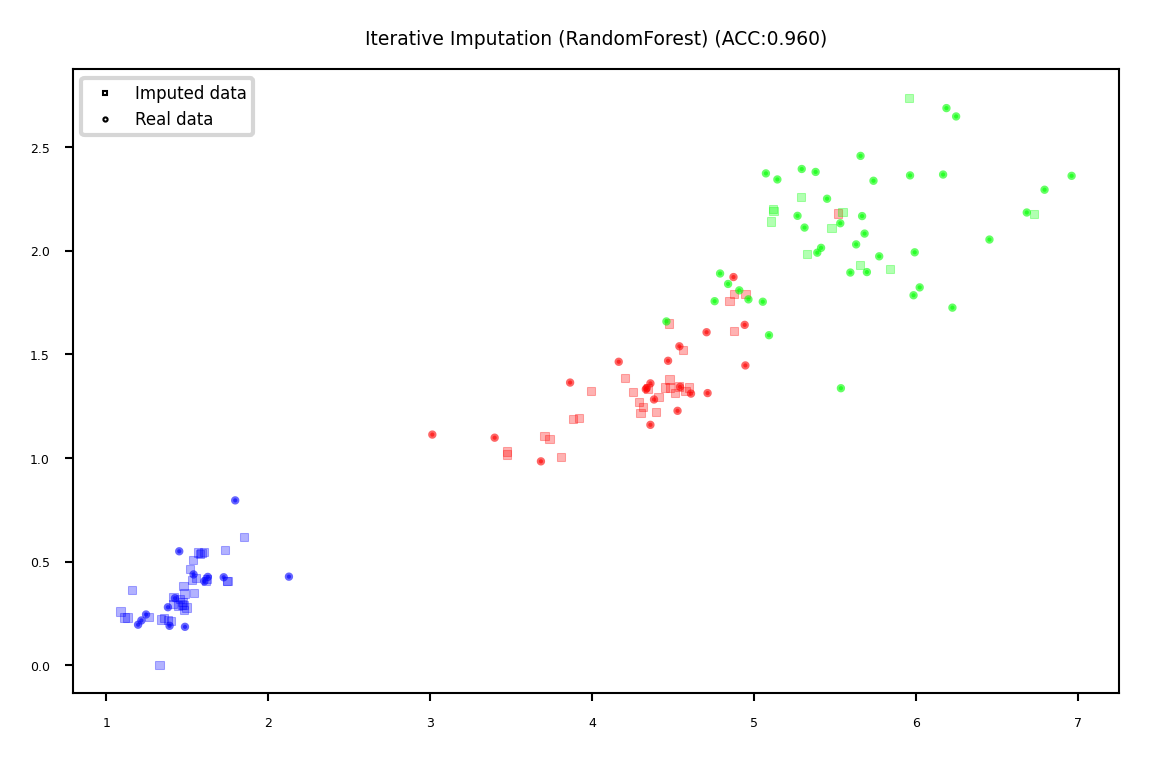
Iterative (model-based) Imputation#
Better known as Multiple Imputation by Chained Equations (MICE)
Iterative approach
Do first imputation (e.g. mean imputation)
Train model (e.g. RandomForest) to predict missing values of a given feature
Train new model on imputed data to predict missing values of the next feature
Repeat \(m\) times in round-robin fashion, leave one feature out at a time
Show code cell source
plot_imputation("Iterative Imputation (RandomForest)")
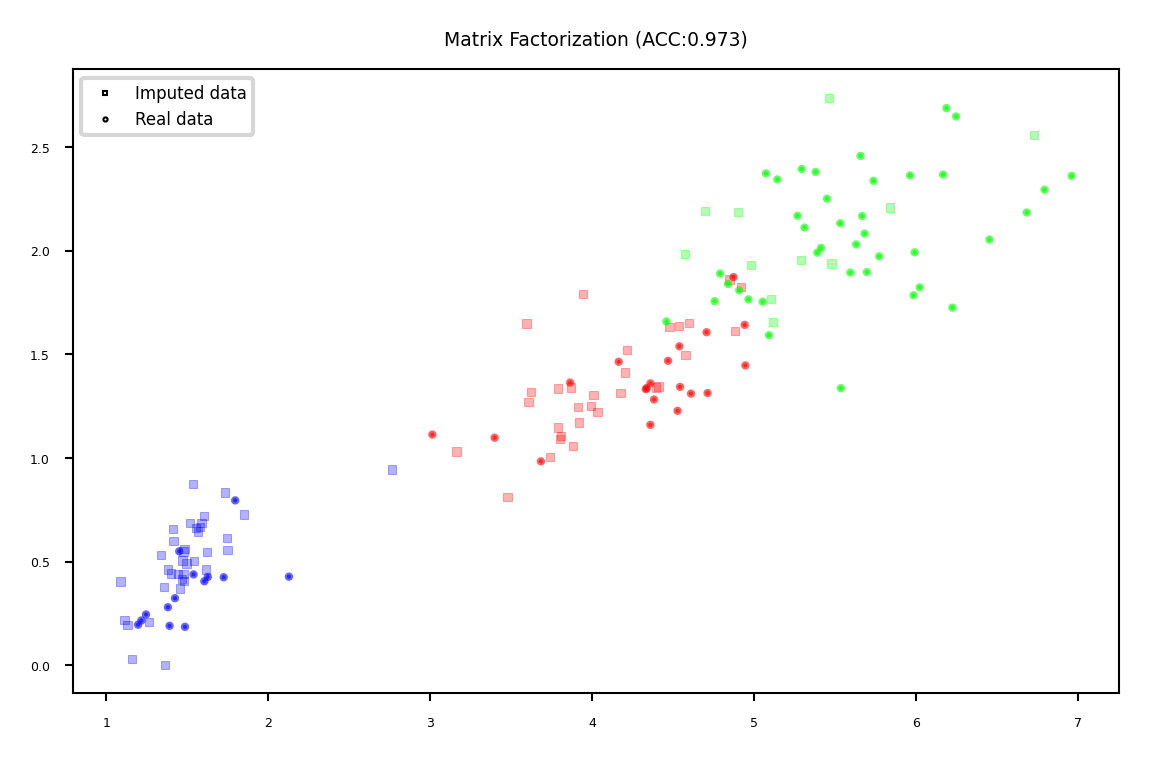
Matrix Factorization#
Basic idea: low-rank approximation
Replace missing values by 0
Factorize \(\mathbf{X}\) with rank \(r\): \(\mathbf{X}^{n\times p}=\mathbf{U}^{n\times r} \mathbf{V}^{r\times p}\)
With n data points and p features
Solved using gradient descent
Recompute \(\mathbf{X}\): now complete
Show code cell source
plot_imputation("Matrix Factorization")
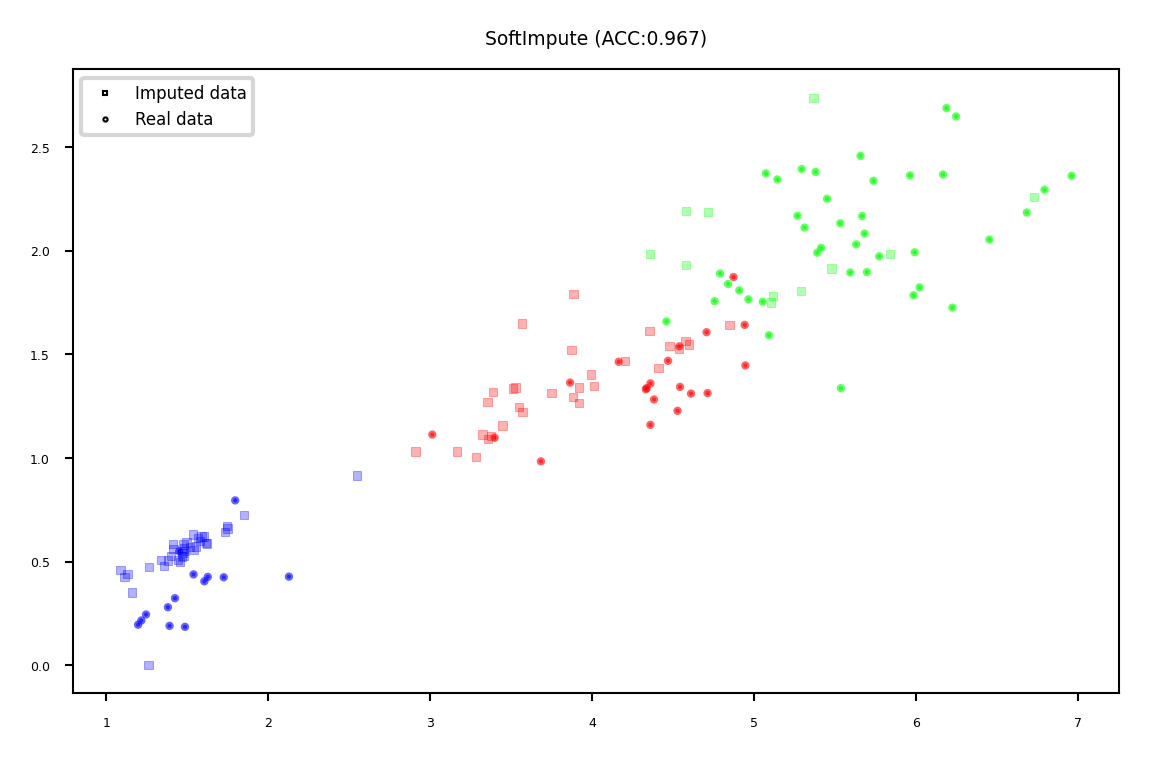
Soft-thresholded Singular Value Decomposition (SVD)#
Same basic idea, but smoother
Replace missing values by 0, compute SVD: \(\mathbf{X}=\mathbf{U} \mathbf{\Sigma} \mathbf{V^{T}}\)
Solved with gradient descent
Reduce eigenvalues by shrinkage factor: \(\lambda_i = s\cdot\lambda_i\)
Recompute \(\mathbf{X}\): now complete
Repeat for \(m\) iterations
Show code cell source
plot_imputation("SoftImpute")
Comparison#
Best method depends on the problem and dataset at hand. Use cross-validation.
Iterative Imputation (MICE) generally works well for missing (completely) at random data
Can be slow if the prediction model is slow
Low-rank approximation techniques scale well to large datasets
Show code cell source
@interact
def compare_imputers(imputer=imputers.keys()):
plot_imputation(imputer=imputer)
Show code cell source
if not interactive:
plot_imputation("Iterative Imputation (RandomForest)")
In practice (scikit-learn)#
Simple replacement:
SimpleImputerStrategies:
mean(numeric),median,most_frequent(categorical)Choose whether to add indicator columns, and how missing values are encoded
imp = SimpleImputer(strategy='mean', missing_values=np.nan, add_indicator=False)
X_complete = imp.fit_transform(X_train)
kNN Imputation:
KNNImputer
imp = KNNImputer(n_neighbors=5)
X_complete = imp.fit_transform(X_train)
Multiple Imputation (MICE):
IterativeImputerChoose estimator (default:
BayesianRidge) and number of iterations (default 10)
imp = IterativeImputer(estimator=RandomForestClassifier(), max_iter=10)
X_complete = imp.fit_transform(X_train)
In practice (fancyimpute)#
Cannot be used in CV pipelines (has
fit_transformbut notransform)Soft-Thresholded SVD:
SoftImputeChoose max number of gradient descent iterations
Choose shrinkage value for eigenvectors (default: \(\frac{1}{N}\))
imp = SoftImpute(max_iter=10, shrinkage_value=None)
X_complete = imp.fit_transform(X)
Low-rank imputation:
MatrixFactorizationChoose rank of the low-rank approximation
Gradient descent hyperparameters: learning rate, epochs,…
Several variants exist
imp = MatrixFactorization(rank=10, learning_rate=0.001, epochs=10000)
X_complete = imp.fit_transform(X)
Handling imbalanced data#
Problem:
You have a majority class with many times the number of examples as the minority class
Or: classes are balanced, but associated costs are not (e.g. FN are worse than FP)
We already covered some ways to resolve this:
Add class weights to the loss function: give the minority class more weight
In practice: set
class_weight='balanced'
Change the prediction threshold to minimize false negatives or false positives
There are also things we can do by preprocessing the data
Resample the data to correct the imbalance
Random or model-based
Generate synthetic samples for the minority class
Build ensembles over different resampled datasets
Combinations of these
Show code cell source
from imblearn.over_sampling import RandomOverSampler, SMOTE, ADASYN
from imblearn.under_sampling import RandomUnderSampler, EditedNearestNeighbours, CondensedNearestNeighbour
from imblearn.ensemble import EasyEnsembleClassifier, BalancedBaggingClassifier
from imblearn.combine import SMOTEENN
from imblearn.pipeline import make_pipeline as make_imb_pipeline # avoid confusion
from sklearn.utils import shuffle
from sklearn.model_selection import cross_validate, train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
# Some imbalanced data
rng = np.random.RandomState(0)
n_samples_1 = 500
n_samples_2 = 50
X_syn = np.r_[1.5 * rng.randn(n_samples_1, 2),
0.5 * rng.randn(n_samples_2, 2) + [1, 1]]
y_syn = np.array([0] * (n_samples_1) + [1] * (n_samples_2))
X_syn, y_syn = shuffle(X_syn, y_syn)
X_syn_train, X_syn_test, y_syn_train, y_syn_test = train_test_split(X_syn, y_syn)
X0min, X0max, X1min, X1max = np.min(X_syn[:,0]), np.max(X_syn[:,0]), np.min(X_syn[:,1]), np.max(X_syn[:,1])
#samplers = [RandomUnderSampler(),EditedNearestNeighbours(),CondensedNearestNeighbour(),RandomOverSampler(),
# SMOTE(), ADASYN(), EasyEnsembleClassifier(), BalancedBaggingClassifier(), SMOTEENN()]
samplers = [RandomUnderSampler(),EditedNearestNeighbours(),RandomOverSampler(),
SMOTE(), ADASYN(), EasyEnsembleClassifier(), BalancedBaggingClassifier(), SMOTEENN()]
learners = [LogisticRegression(), SVC(), RandomForestClassifier()]
def plot_imbalance(sampler=RandomUnderSampler(), sampler2=None, learner=LogisticRegression()):
# Appends multiple undersamplings for plotting purposes
def simulate_bagging(sampler,X_syn, y_syn):
X_resampled, y_resampled = sampler.fit_resample(X_syn, y_syn)
for i in range(10):
X_resampled_i, y_resampled_i = sampler.fit_resample(X_syn, y_syn)
X_resampled = np.append(X_resampled,X_resampled_i, axis=0)
y_resampled = np.append(y_resampled,y_resampled_i, axis=0)
return X_resampled, y_resampled
def build_evaluate(sampler):
# Build new data
X_resampled, y_resampled = X_syn, y_syn
if isinstance(sampler,EasyEnsembleClassifier):
X_resampled, y_resampled = simulate_bagging(RandomUnderSampler(),X_syn, y_syn)
elif isinstance(sampler,BalancedBaggingClassifier):
balancer = RandomUnderSampler(sampling_strategy='all', replacement=True)
X_resampled, y_resampled = simulate_bagging(balancer,X_syn, y_syn)
else:
X_resampled, y_resampled = sampler.fit_resample(X_syn, y_syn)
# Evaluate
if isinstance(sampler,EasyEnsembleClassifier):
pipe = EasyEnsembleClassifier(estimator=learner)
elif isinstance(sampler,BalancedBaggingClassifier):
pipe = BalancedBaggingClassifier(estimator=learner)
else:
pipe = make_imb_pipeline(sampler, learner)
scores = cross_validate(pipe, X_resampled, y_resampled, scoring='roc_auc')['test_score']
return X_resampled, y_resampled, scores
orig_scores = cross_validate(LogisticRegression(), X_syn, y_syn, scoring='roc_auc')['test_score']
# Plot
nr_plots = 2 if sampler2 is None else 3
fig, axes = plt.subplots(1, nr_plots, figsize=(nr_plots*2*fig_scale, 2*fig_scale), subplot_kw={'xticks':(), 'yticks':()})
axes[0].set_title("Original (AUC: {:.3f})".format(np.mean(orig_scores)), fontsize=5)
axes[0].scatter(X_syn[:, 0], X_syn[:, 1], c=plt.cm.tab10(y_syn), alpha=.3)
X_resampled, y_resampled, scores = build_evaluate(sampler)
axes[1].set_title("{} (AUC: {:.3f})".format(sampler.__class__.__name__, np.mean(scores)), fontsize=5);
axes[1].scatter(X_resampled[:, 0], X_resampled[:, 1], c=plt.cm.tab10(y_resampled), alpha=.3)
plt.setp(axes[1], xlim=(X0min, X0max), ylim=(X1min, X1max))
if sampler2 is not None:
X_resampled, y_resampled, scores = build_evaluate(sampler2)
axes[2].set_title("{} (AUC: {:.3f})".format(sampler2.__class__.__name__, np.mean(scores)), fontsize=5);
axes[2].scatter(X_resampled[:, 0], X_resampled[:, 1], c=plt.cm.tab10(y_resampled), alpha=.3)
plt.setp(axes[2], xlim=(X0min, X0max), ylim=(X1min, X1max))
plt.tight_layout()
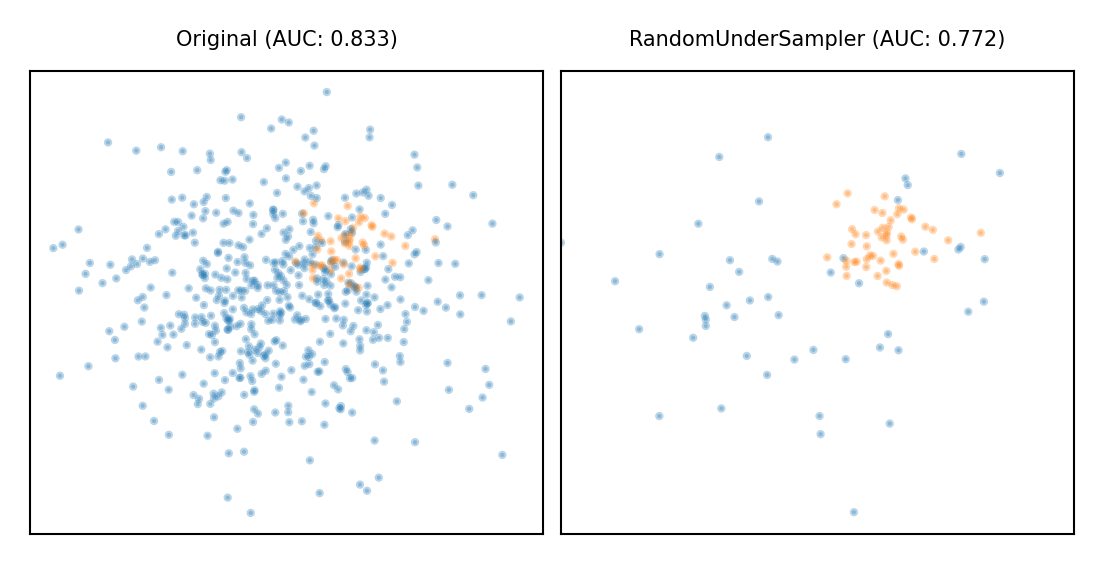
Random Undersampling#
Copy the points from the minority class
Randomly sample from the majority class (with or without replacement) until balanced
Optionally, sample until a certain imbalance ratio (e.g. 1/5) is reached
Multi-class: repeat with every other class
Preferred for large datasets, often yields smaller/faster models with similar performance
Show code cell source
plot_imbalance(RandomUnderSampler())
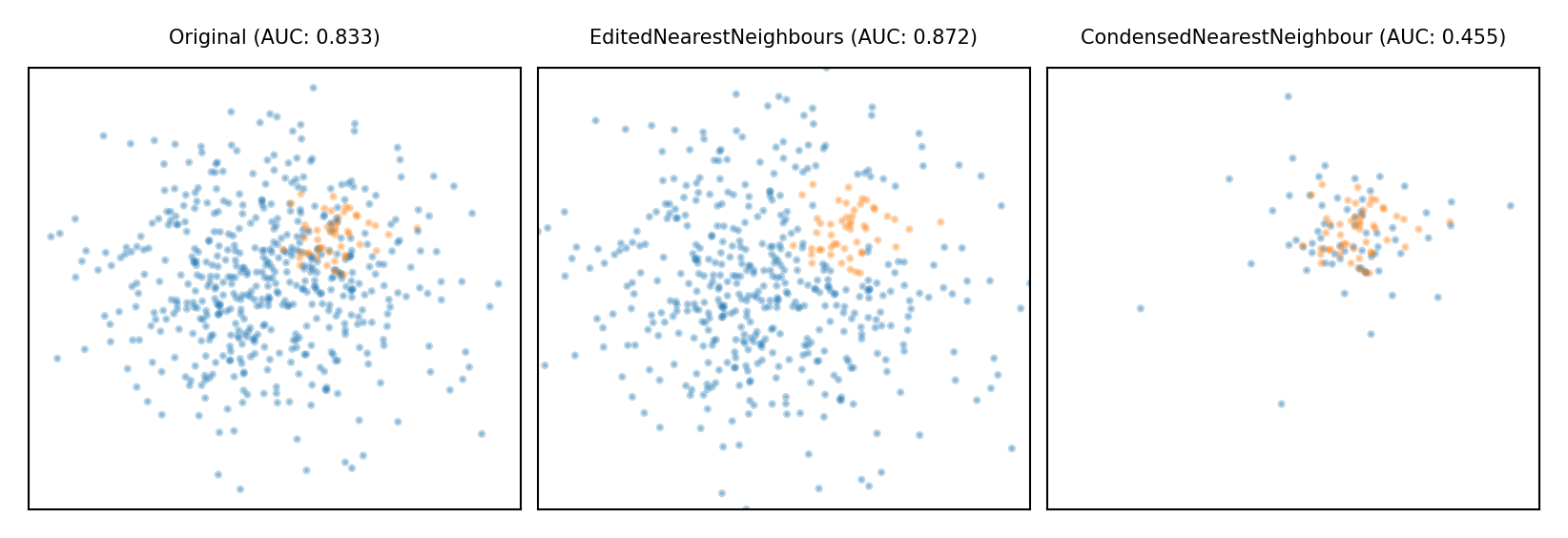
Model-based Undersampling#
Edited Nearest Neighbors
Remove all majority samples that are misclassified by kNN (mode) or that have a neighbor from the other class (all).
Remove their influence on the minority samples
Condensed Nearest Neighbors
Remove all majority samples that are not misclassified by kNN
Focus on only the hard samples
Show code cell source
plot_imbalance(EditedNearestNeighbours(), CondensedNearestNeighbour())
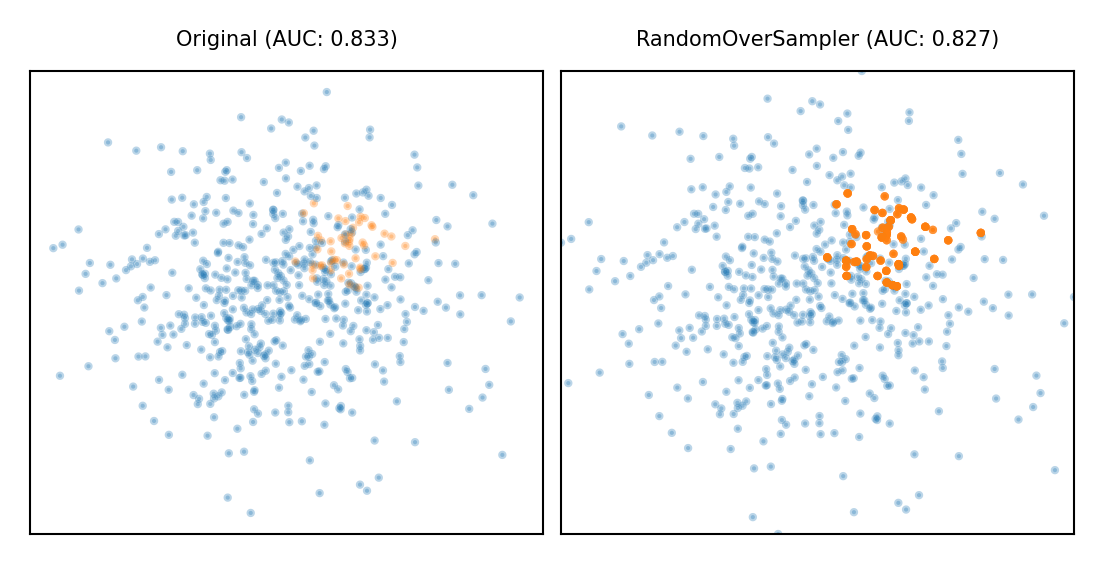
Random Oversampling#
Copy the points from the majority class
Randomly sample from the minority class, with replacement, until balanced
Optionally, sample until a certain imbalance ratio (e.g. 1/5) is reached
Makes models more expensive to train, doens’t always improve performance
Similar to giving minority class(es) a higher weight (and more expensive)
Show code cell source
plot_imbalance(RandomOverSampler())
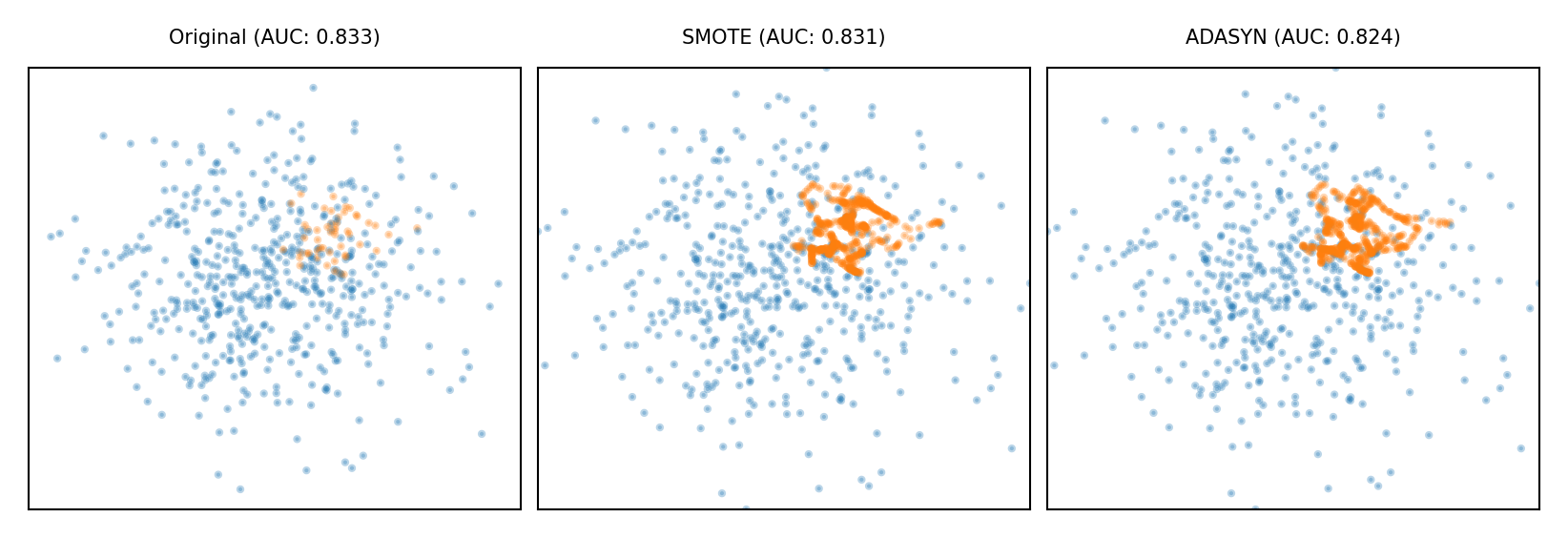
Synthetic Minority Oversampling Technique (SMOTE)#
Repeatedly choose a random minority point and a neighboring minority point
Pick a new, artificial point on the line between them (uniformly)
May bias the data. Be careful never to create artificial points in the test set.
ADASYN (Adaptive Synthetic)
Similar, but starts from ‘hard’ minority points (misclassified by kNN)
Show code cell source
plot_imbalance(SMOTE(), ADASYN())
Combined techniques#
Combines over- and under-sampling
E.g. oversampling with SMOTE, undersampling with Edited Nearest Neighbors (ENN)
SMOTE can generate ‘noisy’ point, close to majority class points
ENN will remove up these majority points to ‘clean up’ the space
Show code cell source
plot_imbalance(SMOTEENN())
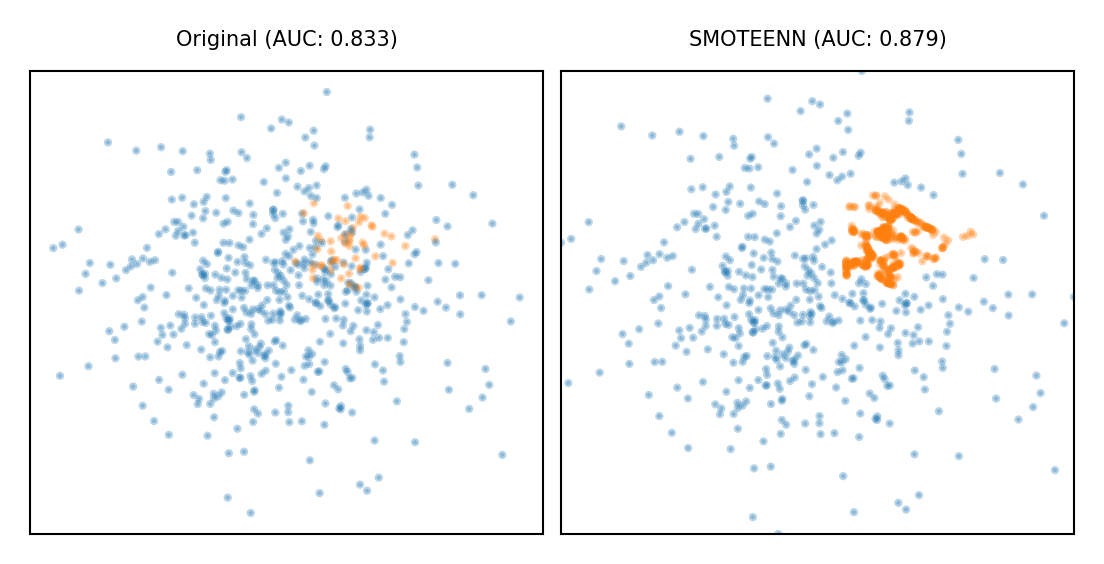
Ensemble Resampling#
Bagged ensemble of balanced base learners. Acts as a learner, not a preprocessor
BalancedBagging: take bootstraps, randomly undersample each, train models (e.g. trees)
Benefits of random undersampling without throwing out so much data
Easy Ensemble: take multiple random undersamplings directly, train models
Traditionally uses AdaBoost as base learner, but can be replaced
Show code cell source
plot_imbalance(EasyEnsembleClassifier(), BalancedBaggingClassifier())
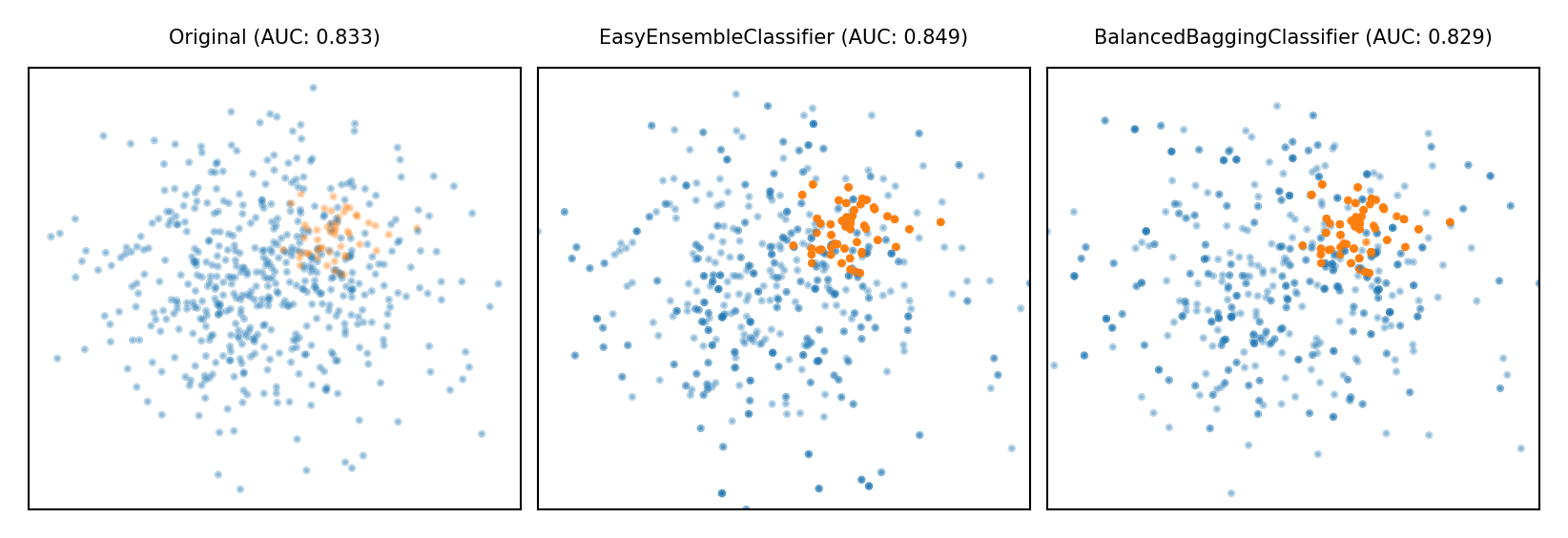
Comparison#
The best method depends on the data (amount of data, imbalance,…)
For a very large dataset, random undersampling may be fine
You still need to choose the appropriate learning algorithms
Don’t forget about class weighting and prediction thresholding
Some combinations are useful, e.g. SMOTE + class weighting + thresholding
Show code cell source
@interact
def compare_imbalance(sampler=samplers, learner=learners):
plot_imbalance(sampler, None, learner)
Show code cell source
if not interactive:
plot_imbalance(EasyEnsembleClassifier())
In practice (imblearn)#
Follows fit-sample paradigm (equivalent of fit-transform, but also affects y)
Undersampling: RandomUnderSampler, EditedNearestNeighbours,…
(Synthetic) Oversampling: RandomOverSampler, SMOTE, ADASYN,…
Combinations: SMOTEENN,…
X_resampled, y_resampled = SMOTE(k_neighbors=5).fit_sample(X, y)
Can be used in imblearn pipelines (not sklearn pipelines)
imblearn pipelines are compatible with GridSearchCV,…
Sampling is only done in
fit(not inpredict)
smote_pipe = make_pipeline(SMOTE(), LogisticRegression())
scores = cross_validate(smote_pipe, X_train, y_train)
param_grid = {"k_neighbors": [3,5,7]}
grid = GridSearchCV(smote_pipe, param_grid=param_grid, X, y)
The ensembling techniques should be used as wrappers
clf = EasyEnsembleClassifier(estimator=SVC()).fit(X_train, y_train)
Real-world data#
The effect of sampling procedures can be unpredictable
Best method can depend on the data and FP/FN trade-offs
SMOTE and ensembling techniques often work well
Show code cell source
from sklearn.metrics import roc_curve, precision_recall_curve
# Datasets
# Try more if you like: ['Speech' ,'mc1','mammography']
# Only showing Speech by default to speed up compute
datasets = ['Speech','mc1','mammography']
roc_curves = {}
for dataset in datasets:
print("Dataset", dataset)
roc_curves[dataset] = {}
# Get data
data_imb = fetch_openml(dataset)
X_imb, y_imb = data_imb.data, data_imb.target
y_imb = LabelEncoder().fit_transform(y_imb)
X_imb_train, X_imb_test, y_imb_train, y_imb_test = train_test_split(X_imb, y_imb, stratify=y_imb, random_state=0)
# Original data
rf = RandomForestClassifier().fit(X_imb_train, y_imb_train)
probs_original = rf.predict_proba(X_imb_test)[:, 1]
fpr_org, tpr_org, _ = roc_curve(y_imb_test, probs_original)
precision, recall, _ = precision_recall_curve(y_imb_test, probs_original)
roc_curves[dataset]["original"] = {}
roc_curves[dataset]["original"]["fpr"] = fpr_org
roc_curves[dataset]["original"]["tpr"] = tpr_org
roc_curves[dataset]["original"]["precision"] = precision
roc_curves[dataset]["original"]["recall"] = recall
# Corrected data
for i, sampler in enumerate(samplers):
sname = sampler.__class__.__name__
print("Evaluating", sname)
# Evaluate
learner = RandomForestClassifier()
if isinstance(sampler,EasyEnsembleClassifier):
pipe = EasyEnsembleClassifier(estimator=learner)
elif isinstance(sampler,BalancedBaggingClassifier):
pipe = BalancedBaggingClassifier(estimator=learner)
else:
pipe = make_imb_pipeline(sampler, learner)
pipe.fit(X_imb_train, y_imb_train)
probs = pipe.predict_proba(X_imb_test)[:, 1]
fpr, tpr, _ = roc_curve(y_imb_test, probs)
precision, recall, _ = precision_recall_curve(y_imb_test, probs)
roc_curves[dataset][sname] = {}
roc_curves[dataset][sname]["id"] = i
roc_curves[dataset][sname]["fpr"] = fpr
roc_curves[dataset][sname]["tpr"] = tpr
roc_curves[dataset][sname]["precision"] = precision
roc_curves[dataset][sname]["recall"] = recall
Dataset Speech
Evaluating RandomUnderSampler
Evaluating EditedNearestNeighbours
Evaluating RandomOverSampler
Evaluating SMOTE
Evaluating ADASYN
Evaluating EasyEnsembleClassifier
Evaluating BalancedBaggingClassifier
Evaluating SMOTEENN
Dataset mc1
Evaluating RandomUnderSampler
Evaluating EditedNearestNeighbours
Evaluating RandomOverSampler
Evaluating SMOTE
Evaluating ADASYN
Evaluating EasyEnsembleClassifier
Evaluating BalancedBaggingClassifier
Evaluating SMOTEENN
Dataset mammography
Evaluating RandomUnderSampler
Evaluating EditedNearestNeighbours
Evaluating RandomOverSampler
Evaluating SMOTE
Evaluating ADASYN
Evaluating EasyEnsembleClassifier
Evaluating BalancedBaggingClassifier
Evaluating SMOTEENN
Show code cell source
# Colors for 9 methods
cm = plt.get_cmap('hsv')
roccol = []
for i in range(1,10):
roccol.append(cm(1.*i/9))
curves = ['ROC','Precision-Recall']
@interact
def roc_imbalance(dataset=datasets, curve=curves):
fig, ax = plt.subplots(figsize=(5*fig_scale, 2*fig_scale))
# Add to plot
curvy = roc_curves[dataset]["original"]
if curve == 'ROC':
ax.plot(curvy["fpr"], curvy["tpr"], label="Original", lw=2, linestyle='-', c='k', alpha=.7)
else:
ax.plot(curvy["recall"], curvy["precision"], label="Original", lw=2, linestyle='-', c='k', alpha=.7)
for method in roc_curves[dataset].keys():
if method != "original":
curvy = roc_curves[dataset][method]
if curve == 'ROC':
ax.plot(curvy["fpr"], curvy["tpr"], label=method, lw=2, linestyle='-', c=roccol[curvy["id"]-1], alpha=.7)
else:
ax.plot(curvy["recall"], curvy["precision"], label=method, lw=2, linestyle='-', c=roccol[curvy["id"]-1], alpha=.7)
if curve == 'ROC':
ax.set_xlabel("FPR")
ax.set_ylabel("TPR")
ax.set_title("RandomForest ROC curve on {} dataset".format(dataset))
ax.legend(ncol=2, loc="lower right")
else:
ax.set_xlabel("Recall")
ax.set_ylabel("Precision")
ax.set_title("RandomForest PR curve on {} dataset".format(dataset))
ax.legend(ncol=2, loc="lower left")
plt.tight_layout()
Show code cell source
if not interactive:
roc_imbalance(dataset='Speech', curve='ROC')
Summary#
Data preprocessing is a crucial part of machine learning
Scaling is important for many distance-based methods (e.g. kNN, SVM, Neural Nets)
Categorical encoding is necessary for numeric methods (or implementations)
Selecting features can speed up models and reduce overfitting
Feature engineering is often useful for linear models
It is often better to impute missing data than to remove data
Imbalanced datasets require extra care to build useful models
Pipelines allow us to encapsulate multiple steps in a convenient way
Avoids data leakage, crucial for proper evaluation
Choose the right preprocessing steps and models in your pipeline
Cross-validation helps, but the search space is huge
Smarter techniques exist to automate this process (AutoML)