Lab 2: Model Selection in scikit-learn#

# General imports
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import openml as oml
from matplotlib import cm

# We can ignore ConvergenceWarnings for illustration purposes
import warnings
warnings.simplefilter(action="ignore", category=UserWarning)

Evaluation procedures#

Holdout#

The simplest procedure is train_test_split, which splits arrays or matrices into random train and test subsets.

from sklearn.datasets import make_blobs
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

# create a synthetic dataset
X, y = make_blobs(centers=2, random_state=0)
# split data and labels into a training and a test set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# Instantiate a model and fit it to the training set
model = LogisticRegression().fit(X_train, y_train)
# evaluate the model on the test set
print("Test set score: {:.2f}".format(model.score(X_test, y_test)))

Test set score: 0.92

Cross-validation#

  • cross_val_score

    • cv parameter defines the kind of cross-validation splits, default is 5-fold CV

    • scoring defines the scoring metric. Also see below.

    • Returns list of all scores. Models are built internally, but not returned

  • cross_validate

    • Similar, but also returns the fit and test times, and allows multiple scoring metrics.

from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression

iris = load_iris()
logreg = LogisticRegression()

scores = cross_val_score(logreg, iris.data, iris.target, cv=5)
print("Cross-validation scores: {}".format(scores))
print("Average cross-validation score: {:.2f}".format(scores.mean()))
print("Variance in cross-validation score: {:.4f}".format(np.var(scores)))

Cross-validation scores: [0.96666667 1.         0.93333333 0.96666667 1.        ]
Average cross-validation score: 0.97
Variance in cross-validation score: 0.0006

Custom CV splits#

from sklearn.model_selection import KFold, StratifiedKFold
kfold = KFold(n_splits=5)
print("Cross-validation scores KFold(n_splits=5):\n{}".format(
      cross_val_score(logreg, iris.data, iris.target, cv=kfold)))
skfold = StratifiedKFold(n_splits=5, shuffle=True)
print("Cross-validation scores StratifiedKFold(n_splits=5, shuffle=True):\n{}".format(
      cross_val_score(logreg, iris.data, iris.target, cv=skfold)))

Cross-validation scores KFold(n_splits=5):
[1.         1.         0.86666667 0.93333333 0.83333333]
Cross-validation scores StratifiedKFold(n_splits=5, shuffle=True):
[0.93333333 0.93333333 1.         0.96666667 0.96666667]

from sklearn.model_selection import LeaveOneOut
loo = LeaveOneOut()
scores = cross_val_score(logreg, iris.data, iris.target, cv=loo)
print("Number of cv iterations: ", len(scores))
print("Mean accuracy: {:.2f}".format(scores.mean()))

Number of cv iterations:  150
Mean accuracy: 0.97

Shuffle-split#

These shuffle the data before splitting it.

  • ShuffleSplit and StratifiedShuffleSplit (recommended for classification)

  • train_size and test_size can be absolute numbers or a percentage of the total dataset

from sklearn.model_selection import ShuffleSplit, StratifiedShuffleSplit
shuffle_split = StratifiedShuffleSplit(test_size=.5, train_size=.5, n_splits=10)
scores = cross_val_score(logreg, iris.data, iris.target, cv=shuffle_split)
print("Cross-validation scores:\n{}".format(scores))

Cross-validation scores:
[0.93333333 0.98666667 0.97333333 0.94666667 0.90666667 0.94666667
 0.98666667 0.96       0.96       0.96      ]

Grouped cross-validation#

  • Add an array with group membership to cross_val_scores

  • Use GroupKFold with the number of groups as CV procedure

from sklearn.model_selection import GroupKFold
# create synthetic dataset
X, y = make_blobs(n_samples=12, random_state=0)
# the first three samples belong to the same group, etc.
groups = [0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3]
scores = cross_val_score(logreg, X, y, groups=groups, cv=GroupKFold(n_splits=4))
print("Cross-validation scores :\n{}".format(scores))

Cross-validation scores :
[0.66666667 0.66666667 1.         0.66666667]

Evaluation Metrics#

Binary classification#

  • confusion_matrix returns a matrix counting how many test examples are predicted correctly or ‘confused’ with other metrics.

  • sklearn.metrics contains implementations many of the metrics discussed in class

    • They are all implemented so that ‘higher is better’.

  • accuracy_score computes accuracy explictly

  • classification_report returns a table of binary measures, per class, and aggregated according to different aggregation functions.

from sklearn.metrics import accuracy_score, confusion_matrix, classification_report, f1_score
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
data = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
    data.data, data.target, stratify=data.target, random_state=0)
lr = LogisticRegression().fit(X_train, y_train)
y_pred = lr.predict(X_test)

print("confusion_matrix(y_test, y_pred): \n", confusion_matrix(y_test, y_pred))
print("accuracy_score(y_test, y_pred): ", accuracy_score(y_test, y_pred))
print("model.score(X_test, y_test): ", lr.score(X_test, y_test))

confusion_matrix(y_test, y_pred): 
 [[48  5]
 [ 5 85]]
accuracy_score(y_test, y_pred):  0.9300699300699301
model.score(X_test, y_test):  0.9300699300699301

plt.rcParams['figure.dpi'] = 100 
print(classification_report(y_test, lr.predict(X_test)))

              precision    recall  f1-score   support

           0       0.91      0.91      0.91        53
           1       0.94      0.94      0.94        90

    accuracy                           0.93       143
   macro avg       0.93      0.93      0.93       143
weighted avg       0.93      0.93      0.93       143

You can explictly define the averaging function for class-level metrics

pred = lr.predict(X_test)
print("Micro average f1 score: {:.3f}".format(f1_score(y_test, pred, average="micro")))
print("Weighted average f1 score: {:.3f}".format(f1_score(y_test, pred, average="weighted")))
print("Macro average f1 score: {:.3f}".format(f1_score(y_test, pred, average="macro")))

Micro average f1 score: 0.930
Weighted average f1 score: 0.930
Macro average f1 score: 0.925

Probabilistic predictions#

To retrieve the uncertainty in the prediction, scikit-learn offers 2 functions. Often, both are available for every learner, but not always.

  • decision_function: returns floating point (-Inf,Inf) value for each prediction

  • predict_proba: returns probability [0,1] for each prediction

You can also use these to compute any metric with non-standard thresholds

print("Threshold -0.8")
y_pred_lower_threshold = lr.decision_function(X_test) > -.8
print(classification_report(y_test, y_pred_lower_threshold))  

Threshold -0.8
              precision    recall  f1-score   support

           0       0.94      0.89      0.91        53
           1       0.94      0.97      0.95        90

    accuracy                           0.94       143
   macro avg       0.94      0.93      0.93       143
weighted avg       0.94      0.94      0.94       143

Uncertainty in multi-class classification#

  • decision_function and predict_proba also work in the multiclass setting

  • always have shape (n_samples, n_classes)

  • Example on the Iris dataset, which has 3 classes:

from sklearn.datasets import load_iris

iris = load_iris()
X_train2, X_test2, y_train2, y_test2 = train_test_split(
    iris.data, iris.target, random_state=42)

lr2 = LogisticRegression()
lr2 = lr2.fit(X_train2, y_train2)

print("Decision function:\n{}".format(lr2.decision_function(X_test2)[:6, :]))
# show the first few entries of predict_proba
print("Predicted probabilities:\n{}".format(lr2.predict_proba(X_test2)[:6]))

Decision function:
[[ -3.03499211   2.29425161   0.7407405 ]
 [  5.91897372   3.09086147  -9.0098352 ]
 [-10.05185099   1.87457159   8.17727941]
 [ -2.73279105   2.03622549   0.69656555]
 [ -3.73730572   2.47556657   1.26173915]
 [  6.03557844   3.0345983   -9.07017674]]
Predicted probabilities:
[[3.98547105e-03 8.22130578e-01 1.73883951e-01]
 [9.44175894e-01 5.58237959e-02 3.10136994e-07]
 [1.20891186e-08 1.82799143e-03 9.98171996e-01]
 [6.68180705e-03 7.87139122e-01 2.06179071e-01]
 [1.54224758e-03 7.69786431e-01 2.28671321e-01]
 [9.52618137e-01 4.73816007e-02 2.62163802e-07]]

Precision-Recall and ROC curves#

  • precision_recall_curve returns all precision and recall values for all possible thresholds

  • roc_curve does the same for TPR and FPR.

  • The average precision score is returned by the average_precision_score measure

  • The area under the ROC curve is returned by the roc_auc_score measure

    • Don’t use auc (this uses a less accurate trapezoidal rule)

    • Require a decision function or predict_proba.

from sklearn.metrics import precision_recall_curve
precision, recall, thresholds = precision_recall_curve(
    y_test, lr.decision_function(X_test))

from sklearn.metrics import average_precision_score
ap_pp = average_precision_score(y_test, lr.predict_proba(X_test)[:, 1])
ap_df = average_precision_score(y_test, lr.decision_function(X_test))
print("Average precision of logreg: {:.3f}".format(ap_df))

Average precision of logreg: 0.995

from sklearn.metrics import roc_auc_score
rf_auc = roc_auc_score(y_test, lr.predict_proba(X_test)[:, 1])
svc_auc = roc_auc_score(y_test, lr.decision_function(X_test))
print("AUC for Random Forest: {:.3f}".format(rf_auc))
print("AUC for SVC: {:.3f}".format(svc_auc))

AUC for Random Forest: 0.991
AUC for SVC: 0.991

Multi-class prediction#

  • Build C models, one for every class vs all others

  • Use micro-, macro-, or weighted averaging

print("Micro average f1 score: {:.3f}".format(f1_score(y_test, pred, average="micro")))
print("Weighted average f1 score: {:.3f}".format(f1_score(y_test, pred, average="weighted")))
print("Macro average f1 score: {:.3f}".format(f1_score(y_test, pred, average="macro")))

Micro average f1 score: 0.930
Weighted average f1 score: 0.930
Macro average f1 score: 0.925

Using evaluation metrics in model selection#

  • You typically want to use AUC or other relevant measures in cross_val_score and GridSearchCV instead of the default accuracy.

  • scikit-learn makes this easy through the scoring argument

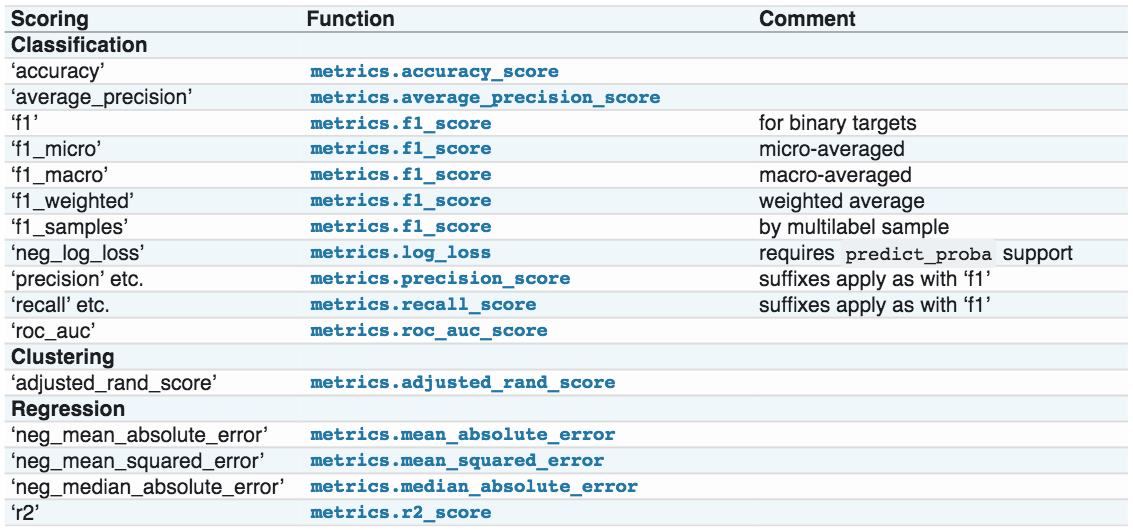
scorers

Or simply look up like this:

from sklearn.metrics import SCORERS
print("Available scorers:\n{}".format(sorted(SCORERS.keys())))

Available scorers:
['accuracy', 'adjusted_mutual_info_score', 'adjusted_rand_score', 'average_precision', 'balanced_accuracy', 'completeness_score', 'explained_variance', 'f1', 'f1_macro', 'f1_micro', 'f1_samples', 'f1_weighted', 'fowlkes_mallows_score', 'homogeneity_score', 'jaccard', 'jaccard_macro', 'jaccard_micro', 'jaccard_samples', 'jaccard_weighted', 'max_error', 'mutual_info_score', 'neg_brier_score', 'neg_log_loss', 'neg_mean_absolute_error', 'neg_mean_absolute_percentage_error', 'neg_mean_gamma_deviance', 'neg_mean_poisson_deviance', 'neg_mean_squared_error', 'neg_mean_squared_log_error', 'neg_median_absolute_error', 'neg_root_mean_squared_error', 'normalized_mutual_info_score', 'precision', 'precision_macro', 'precision_micro', 'precision_samples', 'precision_weighted', 'r2', 'rand_score', 'recall', 'recall_macro', 'recall_micro', 'recall_samples', 'recall_weighted', 'roc_auc', 'roc_auc_ovo', 'roc_auc_ovo_weighted', 'roc_auc_ovr', 'roc_auc_ovr_weighted', 'top_k_accuracy', 'v_measure_score']

Cross-validation with AUC

from sklearn.model_selection import cross_val_score, GridSearchCV
from sklearn .svm import SVC
from sklearn.datasets import load_digits
digits = load_digits()

# default scoring for classification is accuracy
print("Default scoring: {}".format(
      cross_val_score(SVC(), digits.data, digits.target == 9)))
# providing scoring="accuracy" doesn't change the results
explicit_accuracy =  cross_val_score(SVC(), digits.data, digits.target == 9, 
                                     scoring="accuracy")
print("Explicit accuracy scoring: {}".format(explicit_accuracy))
roc_auc =  cross_val_score(SVC(), digits.data, digits.target == 9,
                           scoring="roc_auc")
print("AUC scoring: {}".format(roc_auc))

Default scoring: [0.975      0.99166667 1.         0.99442897 0.98050139]
Explicit accuracy scoring: [0.975      0.99166667 1.         0.99442897 0.98050139]
AUC scoring: [0.99717078 0.99854252 1.         0.999828   0.98400413]

Hyperparameter tuning#

Now that we know how to evaluate models, we can improve them by tuning their hyperparameters

Nested cross-validation#

  • Nested cross-validation:

    • Outer loop: split data in training and test sets

    • Inner loop: run grid search, splitting the training data into train and validation sets

  • Result is a just a list of scores

    • There will be multiple optimized models and hyperparameter settings (not returned)

  • To apply on future data, we need to train GridSearchCV on all data again

scores = cross_val_score(GridSearchCV(SVC(), param_grid, cv=5),
                         iris.data, iris.target, cv=5)
print("Cross-validation scores: ", scores)
print("Mean cross-validation score: ", scores.mean())

Cross-validation scores:  [0.96666667 1.         0.9        0.96666667 1.        ]
Mean cross-validation score:  0.9666666666666668