Recap: Data preprocessing

Recap: Data preprocessing#

Basic data transformation techniques

Joaquin Vanschoren

Data transformations covered here#

Scaling and power transformations
Unsupervised feature selection ()
- Feature engineering (e.g. binning, polynomial features,…)
- Handling missing data
- Handling imbalanced data
- Dimensionality reduction (e.g. PCA)
- Learned embeddings (e.g. for text)
Seek the best combinations of transformations and learning methods
- Often done empirically, using cross-validation
- Make sure that there is no data leakage during this process!

Scaling#

Use when different numeric features have different scales (different range of values)
- Features with much higher values may overpower the others
Goal: bring them all within the same range
Different methods exist

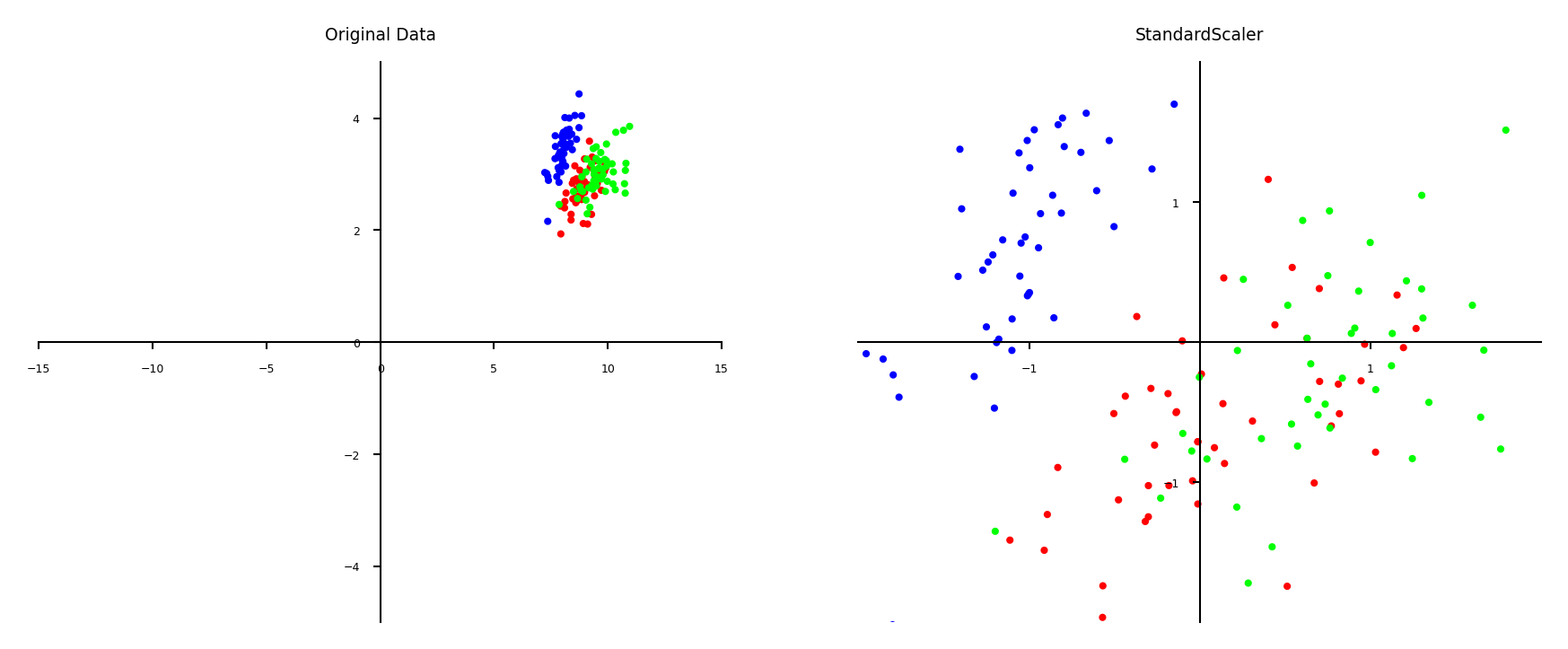
../_images/5d83d4562af7959a5815b6f1586526469f4129fd7a36765f669dda38b4306011.png

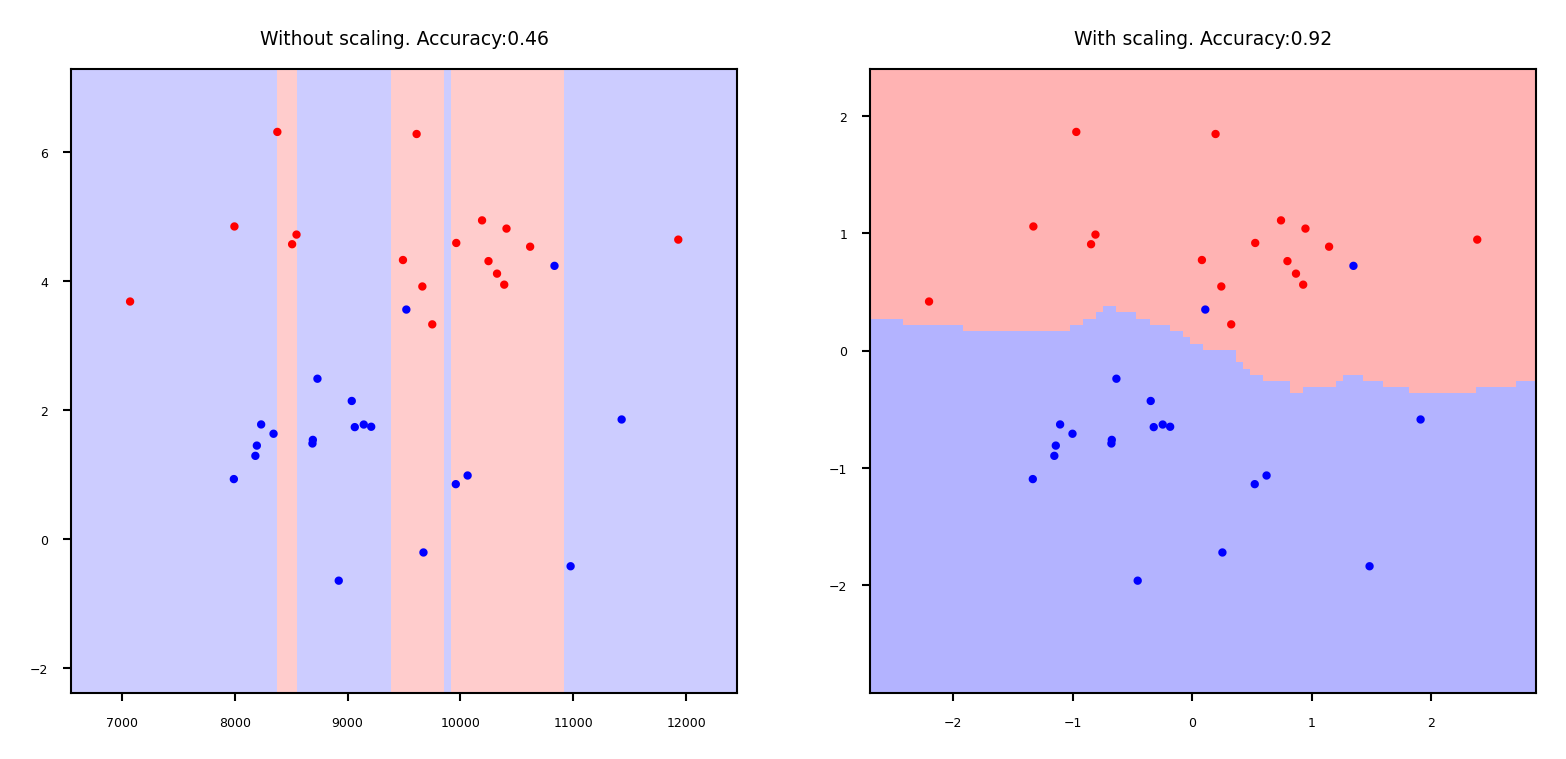
Why do we need scaling?#

KNN: Distances depend mainly on feature with larger values
SVMs: (kernelized) dot products are also based on distances
Linear model: Feature scale affects regularization
- Weights have similar scales, more interpretable

Show code cell source Hide code cell source

from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.base import clone

# Example by Andreas Mueller, with some tweaks
def plot_2d_classification(classifier, X, fill=False, ax=None, eps=None, alpha=1):
    # multiclass                                                                  
    if eps is None:                                                               
        eps = X.std(axis=0) / 2.
    else:
        eps = np.array([eps, eps])

    if ax is None:                                                                
        ax = plt.gca()                                                            

    x_min, x_max = X[:, 0].min() - eps[0], X[:, 0].max() + eps[0]
    y_min, y_max = X[:, 1].min() - eps[1], X[:, 1].max() + eps[1]
    # these should be 1000 but knn predict is unnecessarily slow
    xx = np.linspace(x_min, x_max, 100)                                          
    yy = np.linspace(y_min, y_max, 100)                                          

    X1, X2 = np.meshgrid(xx, yy)                                                  
    X_grid = np.c_[X1.ravel(), X2.ravel()]                                        
    decision_values = classifier.predict(X_grid)                                  
    ax.imshow(decision_values.reshape(X1.shape), extent=(x_min, x_max,            
                                                       y_min, y_max),             
            aspect='auto', origin='lower', alpha=alpha, cmap=plt.cm.bwr)     

clfs = [KNeighborsClassifier(), SVC(), LinearSVC(), LogisticRegression(C=10)]

@interact
def plot_scaling_effect(classifier=clfs, show_test=[False,True]):
    X, y = make_blobs(centers=2, random_state=4, n_samples=50)
    X = X * np.array([1000, 1])
    y[7], y[27] = 0, 0 
    X_train, X_test, y_train, y_test = train_test_split(X,y, stratify=y, random_state=1)
    
    clf2 = clone(classifier)
    clf_unscaled = classifier.fit(X_train, y_train)

    fig, axes = plt.subplots(1, 2, figsize=(7*fig_scale, 3*fig_scale))
    axes[0].scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap='bwr', label="train")
    axes[0].set_title("Without scaling. Accuracy:{:.2f}".format(clf_unscaled.score(X_test,y_test)))
    if show_test: # Hide test data for simplicity
        axes[0].scatter(X_test[:, 0], X_test[:, 1], c=y_test, marker='^', cmap='bwr', label="test") 
        axes[0].legend()
    
    scaler = StandardScaler().fit(X_train)
    X_train_scaled = scaler.transform(X_train)
    X_test_scaled = scaler.transform(X_test)
    clf_scaled = clf2.fit(X_train_scaled, y_train)

    axes[1].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1], c=y_train, cmap='bwr', label="train")
    axes[1].set_title("With scaling. Accuracy:{:.2f}".format(clf_scaled.score(X_test_scaled,y_test)))   
    if show_test: # Hide test data for simplicity
        axes[1].scatter(X_test_scaled[:, 0], X_test_scaled[:, 1], c=y_test, marker='^', cmap='bwr', label="test")
        axes[1].legend()

    plot_2d_classification(clf_unscaled, X, ax=axes[0], alpha=.2)
    plot_2d_classification(clf_scaled, scaler.transform(X), ax=axes[1], alpha=.3)

../_images/503374d9c151f54d23cfff574515eddc7bb94640c2b994704136ac3bc273e02a.png

Standard scaling (standardization)#

Generally most useful, assumes data is more or less normally distributed
Per feature, subtract the mean value $\mu$, scale by standard deviation $\sigma$
New feature has $\mu=0$ and $\sigma=1$, values can still be arbitrarily large $$\mathbf{x}_{new} = \frac{\mathbf{x} - \mu}{\sigma}$$

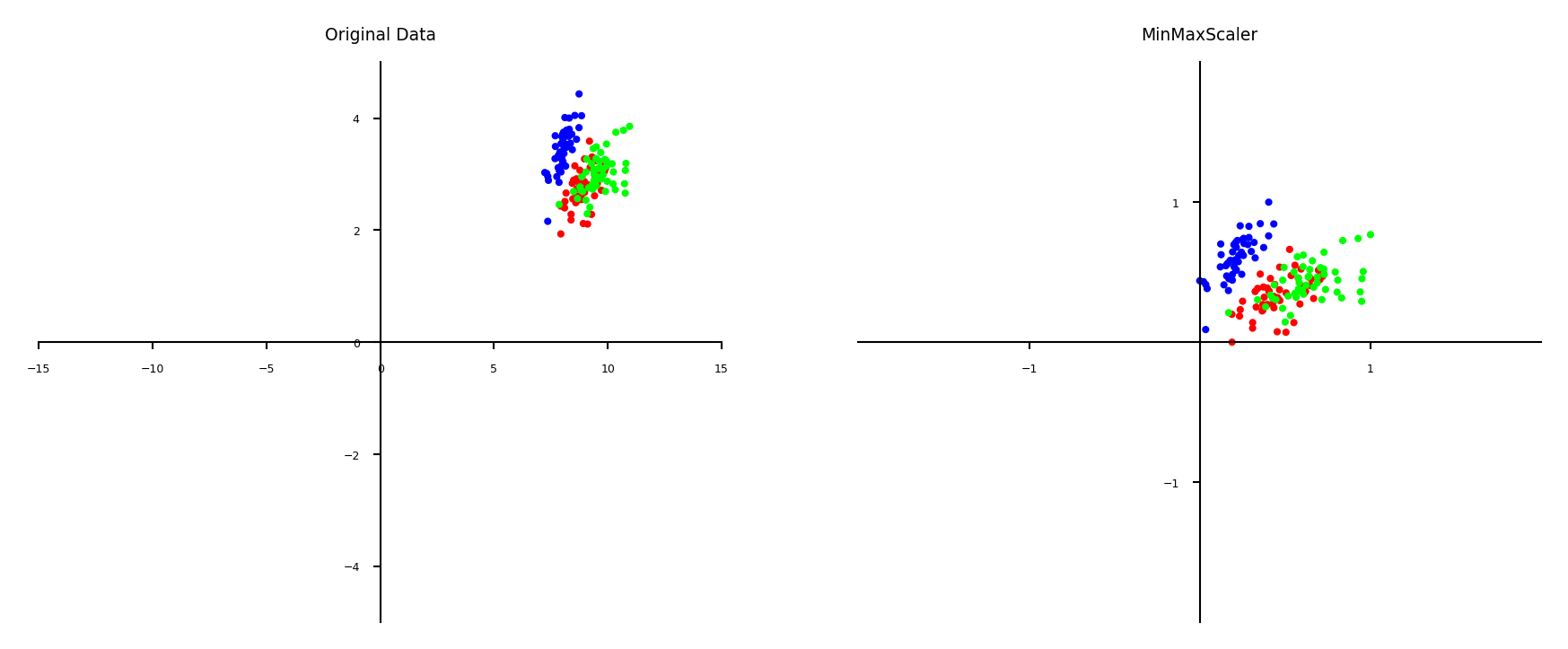
Min-max scaling#

Scales all features between a given $min$ and $max$ value (e.g. 0 and 1)
Makes sense if min/max values have meaning in your data
Sensitive to outliers

\[\mathbf{x}_{new} = \frac{\mathbf{x} - x_{min}}{x_{max} - x_{min}} \cdot (max - min) + min \]

../_images/f86889606574399b60477f9a2ecac135752f51359cea5f61b449c5cd28ff205a.png

Robust scaling#

Subtracts the median, scales between quantiles $q_{25}$ and $q_{75}$
New feature has median 0, $q_{25}=-1$ and $q_{75}=1$
Similar to standard scaler, but ignores outliers

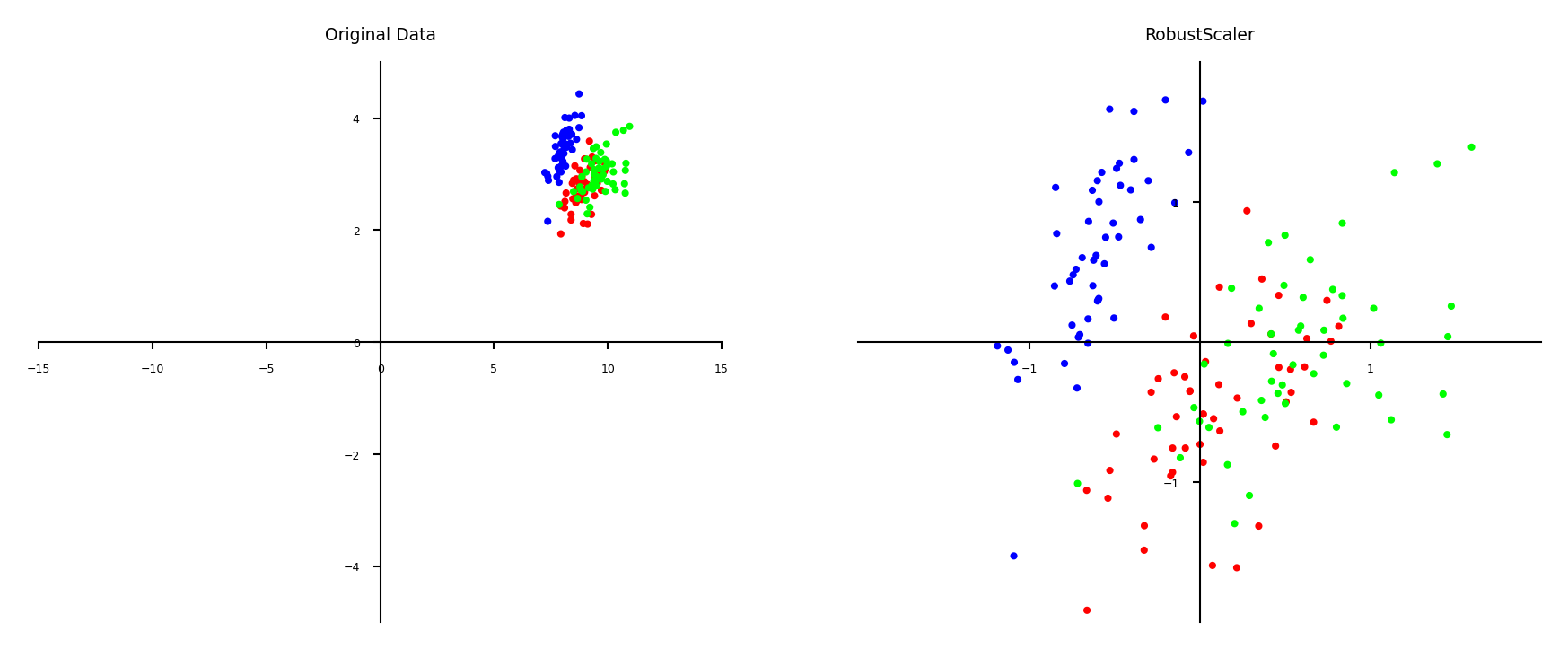
../_images/467b56d3f59dc4f90471ba335c71b2b4799070aa5efde229319ab259bedc596e.png

Normalization#

Makes sure that feature values of each point (each row) sum up to 1 (L1 norm)
- Useful for count data (e.g. word counts in documents)
Can also be used with L2 norm (sum of squares is 1)
- Useful when computing distances in high dimensions
- Normalized Euclidean distance is equivalent to cosine similarity

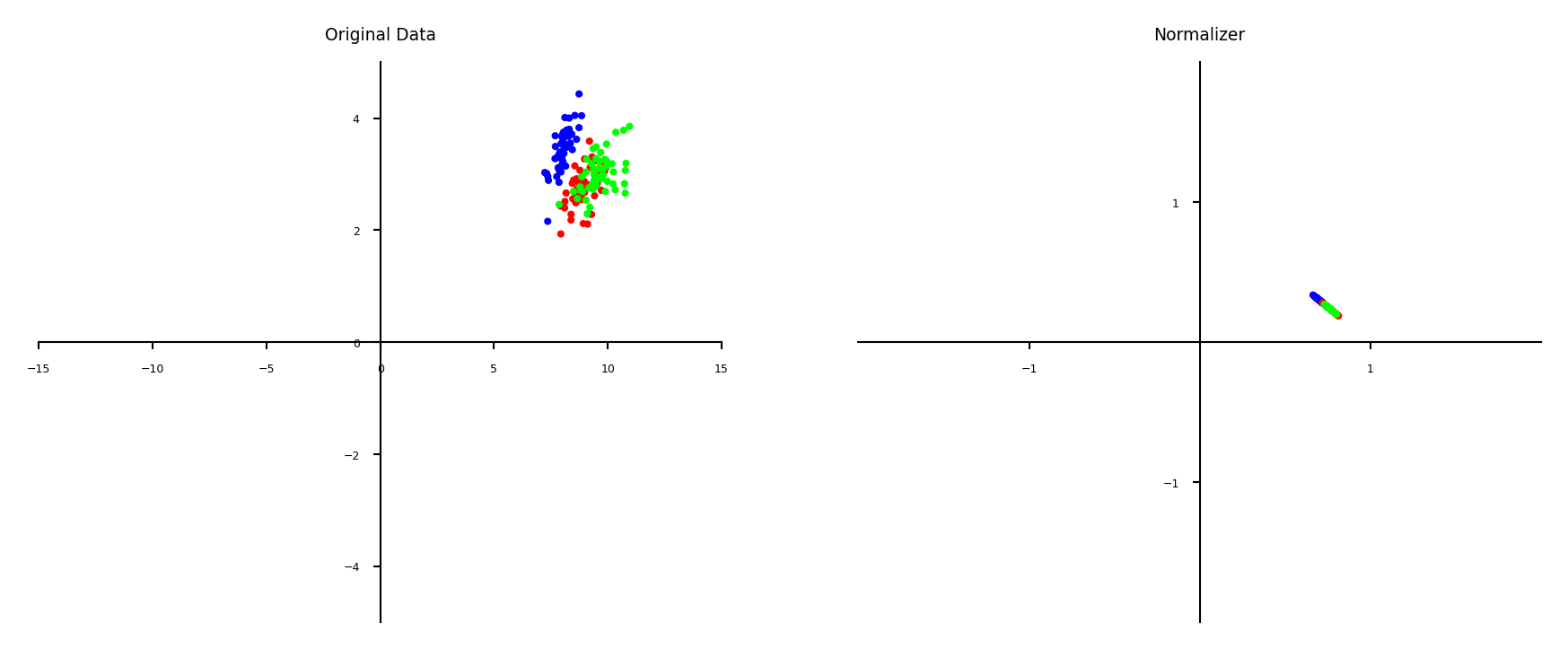
../_images/970be4008720534aa6d57d82dca2c845ae359b8c6c367f86e99c2404abf67b5c.png

Maximum Absolute scaler#

For sparse data (many features, but few are non-zero)
- Maintain sparseness (efficient storage)
Scales all values so that maximum absolute value is 1
Similar to Min-Max scaling without changing 0 values

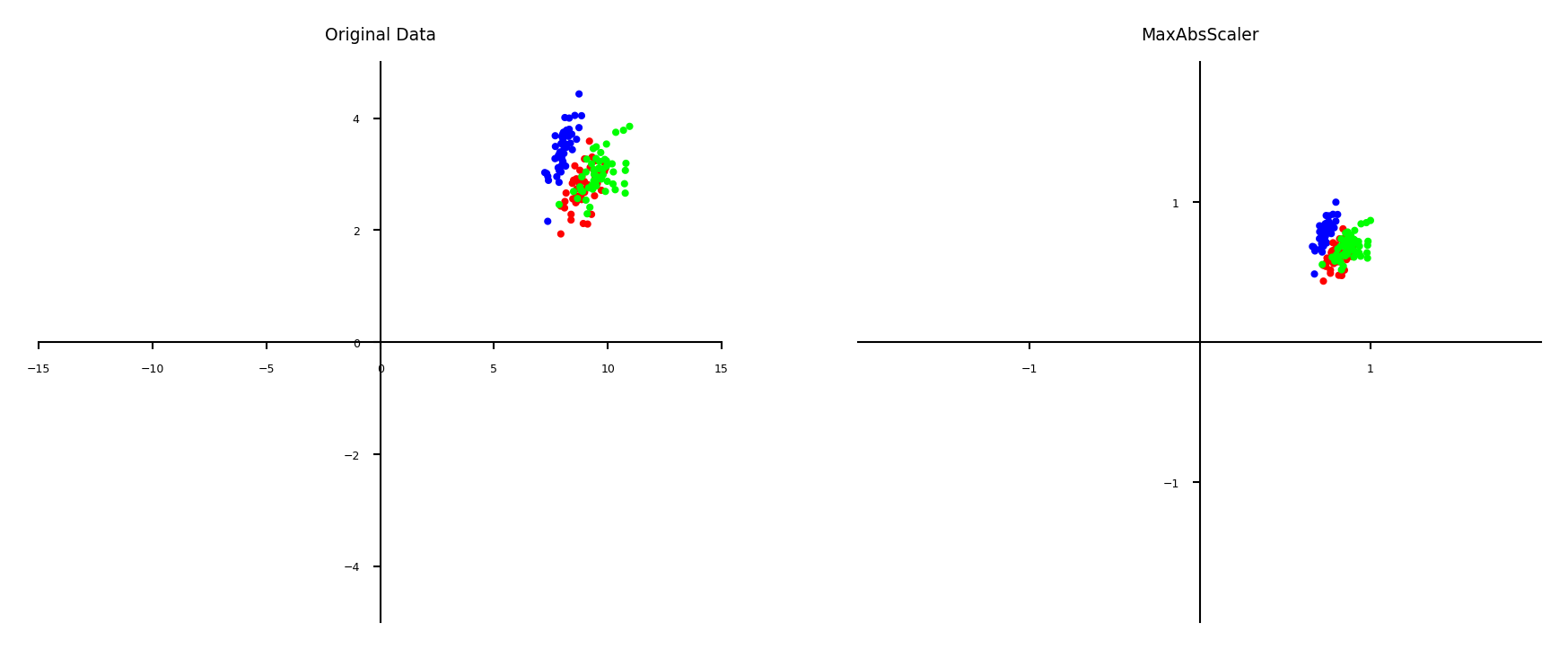
../_images/7bd03995ac1a103bc553eb79870a0a73c018534246700066a78ff7d5a013acf2.png

Automatic Feature Selection#

It can be a good idea to reduce the number of features to only the most useful ones

Simpler models that generalize better (less overfitting)
- Curse of dimensionality (e.g. kNN)
- Even models such as RandomForest can benefit from this
- Sometimes it is one of the main methods to improve models (e.g. gene expression data)
Faster prediction and training
- Training time can be quadratic (or cubic) in number of features
Easier data collection, smaller models (less storage)
More interpretable models: fewer features to look at

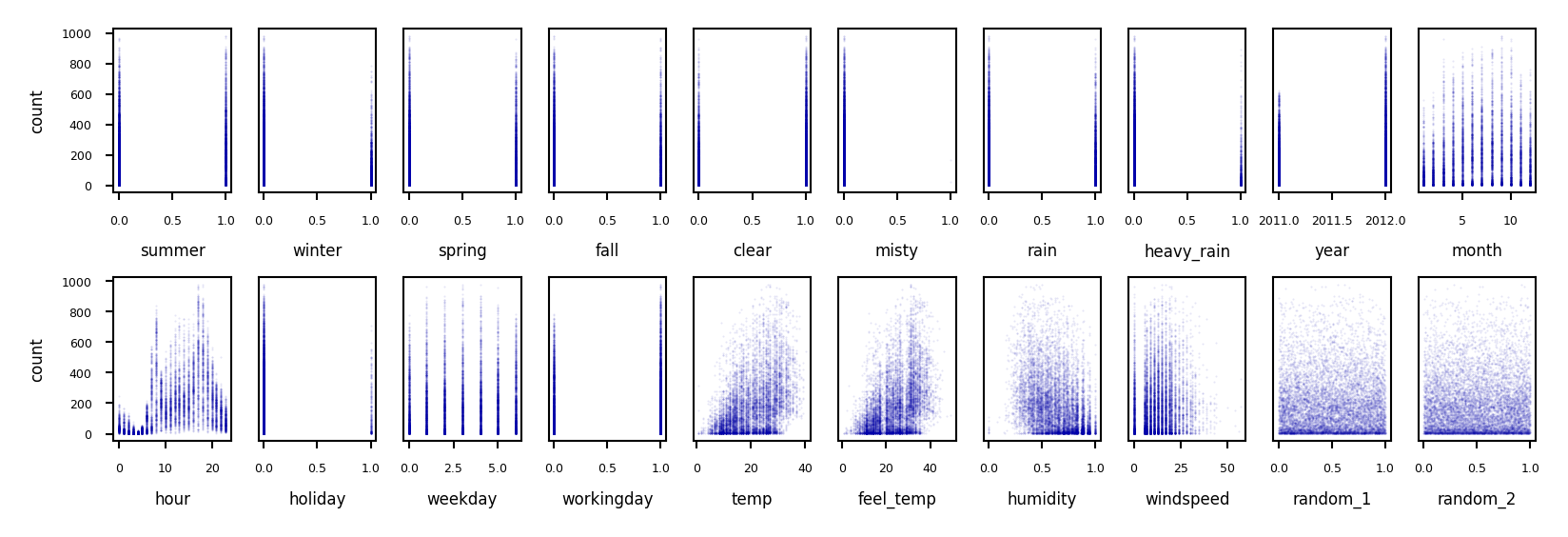
Unsupervised feature selection#

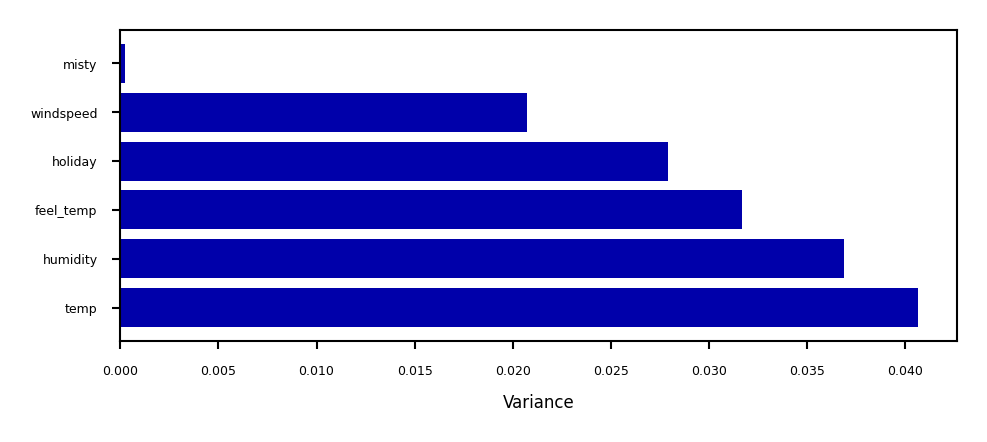
Variance-based
- Remove (near) constant feature: choose a small variance threshold
- Scale features before computing variance!
- Infrequent values may still be important
Covariance-based
- Remove correlated features
- The small differences may actually be important
  - You don’t know because you don’t consider the target

from sklearn.feature_selection import f_regression, SelectPercentile, mutual_info_regression, SelectFromModel, RFE
from tqdm.notebook import trange, tqdm
from sklearn.preprocessing import scale
from sklearn.ensemble import RandomForestRegressor
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import cross_val_score, GridSearchCV



# Pre-compute all importances on bike sharing dataset
# Scaled feature selection thresholds
thresholds = [0.25, 0.5, 0.75, 1]
# Dict to store all data
fs = {}
methods = ['FTest','MutualInformation']
for m in methods:
    fs[m] = {}
    fs[m]['select'] = {}
    fs[m]['cv_score'] = {}

def cv_score(selector):
    model = RandomForestRegressor()
    select_pipe = make_pipeline(StandardScaler(), selector, model)    
    return np.mean(cross_val_score(select_pipe, X_bike, y_bike, cv=3))

# F test
print("Computing F test")
fs['FTest']['label'] = "F test"
fs['FTest']['score'] = f_regression(scale(X_bike),y_bike)[0]
fs['FTest']['scaled_score'] = fs['FTest']['score'] / np.max(fs['FTest']['score'])
for t in tqdm(thresholds):
    selector = SelectPercentile(score_func=f_regression, percentile=t*100).fit(scale(X_bike), y_bike)
    fs['FTest']['select'][t] = selector.get_support()
    fs['FTest']['cv_score'][t] = cv_score(selector)

# Mutual information
print("Computing Mutual information")
fs['MutualInformation']['label'] = "Mutual Information"
fs['MutualInformation']['score'] = mutual_info_regression(scale(X_bike),y_bike,discrete_features=range(13)) # first 13 features are discrete
fs['MutualInformation']['scaled_score'] = fs['MutualInformation']['score'] / np.max(fs['MutualInformation']['score'])
for t in tqdm(thresholds):
    selector = SelectPercentile(score_func=mutual_info_regression, percentile=t*100).fit(scale(X_bike), y_bike)
    fs['MutualInformation']['select'][t] = selector.get_support()
    fs['MutualInformation']['cv_score'][t] = cv_score(selector)
    
def plot_feature_importances(method1='f_test', method2=None, threshold=0.5):
    
    # Plot scores
    x = np.arange(20)
    fig, ax1 = plt.subplots(1, 1, figsize=(4*fig_scale, 1*fig_scale))
    w = 0.3
    imp = fs[method1]
    mask = imp['select'][threshold]
    m1 = ax1.bar(x[mask], imp['scaled_score'][mask], width=w, color='b', align='center')
    ax1.bar(x[~mask], imp['scaled_score'][~mask], width=w, color='b', align='center', alpha=0.3)
    if method2:
        imp2 = fs[method2]
        mask2 = imp2['select'][threshold]
        ax2 = ax1.twinx()
        m2 = ax2.bar(x[mask2] + w, imp2['scaled_score'][mask2], width=w,color='g',align='center')
        ax2.bar(x[~mask2] + w, imp2['scaled_score'][~mask2], width=w,color='g',align='center', alpha=0.3)
        plt.legend([m1, m2],['{} (Ridge R2:{:.2f})'.format(imp['label'],imp['cv_score'][threshold]),
                             '{} (Ridge R2:{:.2f})'.format(imp2['label'],imp2['cv_score'][threshold])], loc='upper left')
    else:
        plt.legend([m1],['{} (Ridge R2:{:.2f})'.format(imp['label'],imp['cv_score'][threshold])], loc='upper left')
    ax1.set_xticks(range(len(bike_names)))
    ax1.set_xticklabels(bike_names, rotation=45, ha="right");
    plt.title("Feature importance (selection threshold {:.2f})".format(threshold))
                        
    plt.show()

Computing F test

Computing Mutual information

../_images/ca5fe0aa1f4c062d46c8154dc8c85db4a8ede50f786b472e2e55c08bcd24cc3d.png

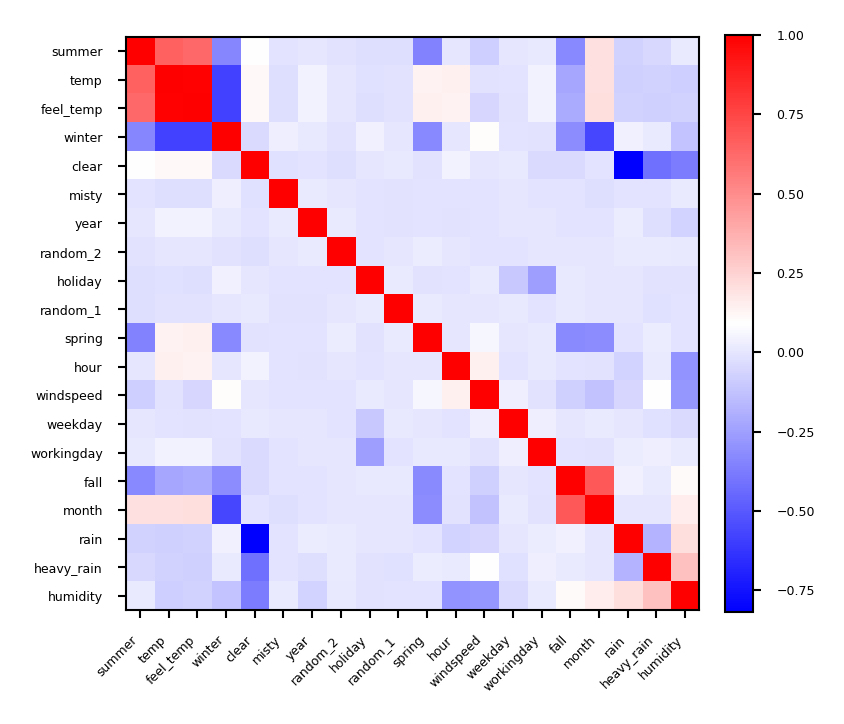
Covariance based feature selection#

Remove features $X_i$ (= $\mathbf{X_{:,i}}$) that are highly correlated (have high correlation coefficient $\rho$) $$\rho (X_1,X_2)={\frac {{\mathrm {cov}}(X_1,X_2)}{\sigma (X_1)\sigma (X_2)}} = {\frac { \frac{1}{N-1} \sum_i (X_{i,1} - \overline{X_1})(X_{i,2} - \overline{X_2}) }{\sigma (X_1)\sigma (X_2)}}$$
Should we remove feel_temp? Or temp? Maybe one correlates more with the target?

../_images/86dc8098df6577705c8558e4cd5379f3d11b195026ec5a2a48bd04d5613abdfc.png

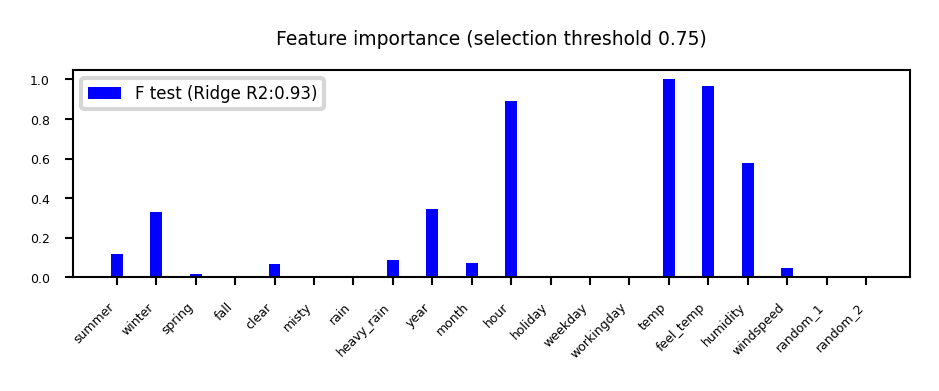
Univariate statistics (F-test)#

Consider each feature individually (univariate), independent of the model that you aim to apply
Use a statistical test: is there a linear statistically significant relationship with the target?
Use F-statistic (or corresponding p value) to rank all features, then select features using a threshold
- Best $k$, best $k$ %, probability of removing useful features (FPR),…
Cannot detect correlations (e.g. temp and feel_temp) or interactions (e.g. binary features)

../_images/c6ecf74f9d4e51ae85a54336d22162583d1d6480d34c27f21bda7815e842b923.png

F-statistic#

For regression: does feature $X_i$ correlate (positively or negatively) with the target $y$? $$\text{F-statistic} = \frac{\rho(X_i,y)^2}{1-\rho(X_i,y)^2} \cdot (N-1)$$
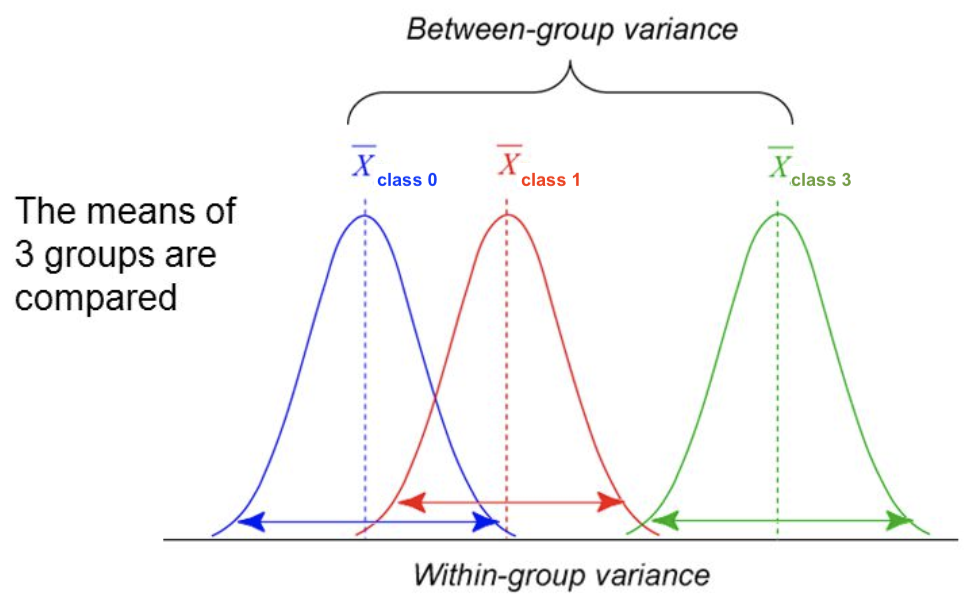
For classification: uses ANOVA: does $X_i$ explain the between-class variance?
- Alternatively, use the $\chi^2$ test (only for categorical features) $$\text{F-statistic} = \frac{\text{within-class variance}}{\text{between-class variance}} =\frac{var(\overline{X_i})}{\overline{var(X_i)}}$$

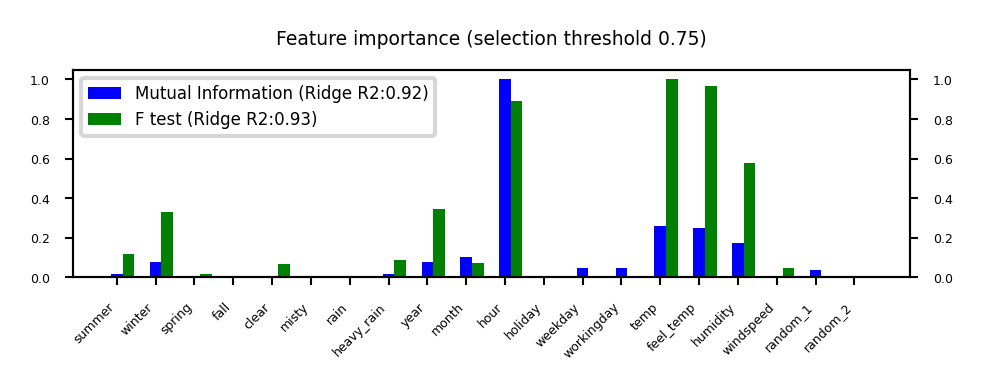
Mutual information#

Measures how much information $X_i$ gives about the target $Y$. In terms of entropy $H$: $$MI(X,Y) = H(X) + H(Y) - H(X,Y)$$
Idea: estimate H(X) as the average distance between a data point and its $k$ Nearest Neighbors
- You need to choose $k$ and say which features are categorical
Captures complex dependencies (e.g. hour, month), but requires more samples to be accurate

../_images/1e161bd430500d01832367dd877ce0f2c8aa3867151289ec34f444ddb6520a66.png

Further techniques#

Many more powerful techniques exist
- Model-based: Random Forests, Linear models, kNN
- Wrapping techniques (black-box search)
- Permutation importance
See the Data Preprocessing lecture.

Feature Engineering#

Create new features based on existing ones
- Polynomial features
- Interaction features
- Binning
Mainly useful for simple models (e.g. linear models)
- Other models can learn interations themselves
- But may be slower, less robust than linear models

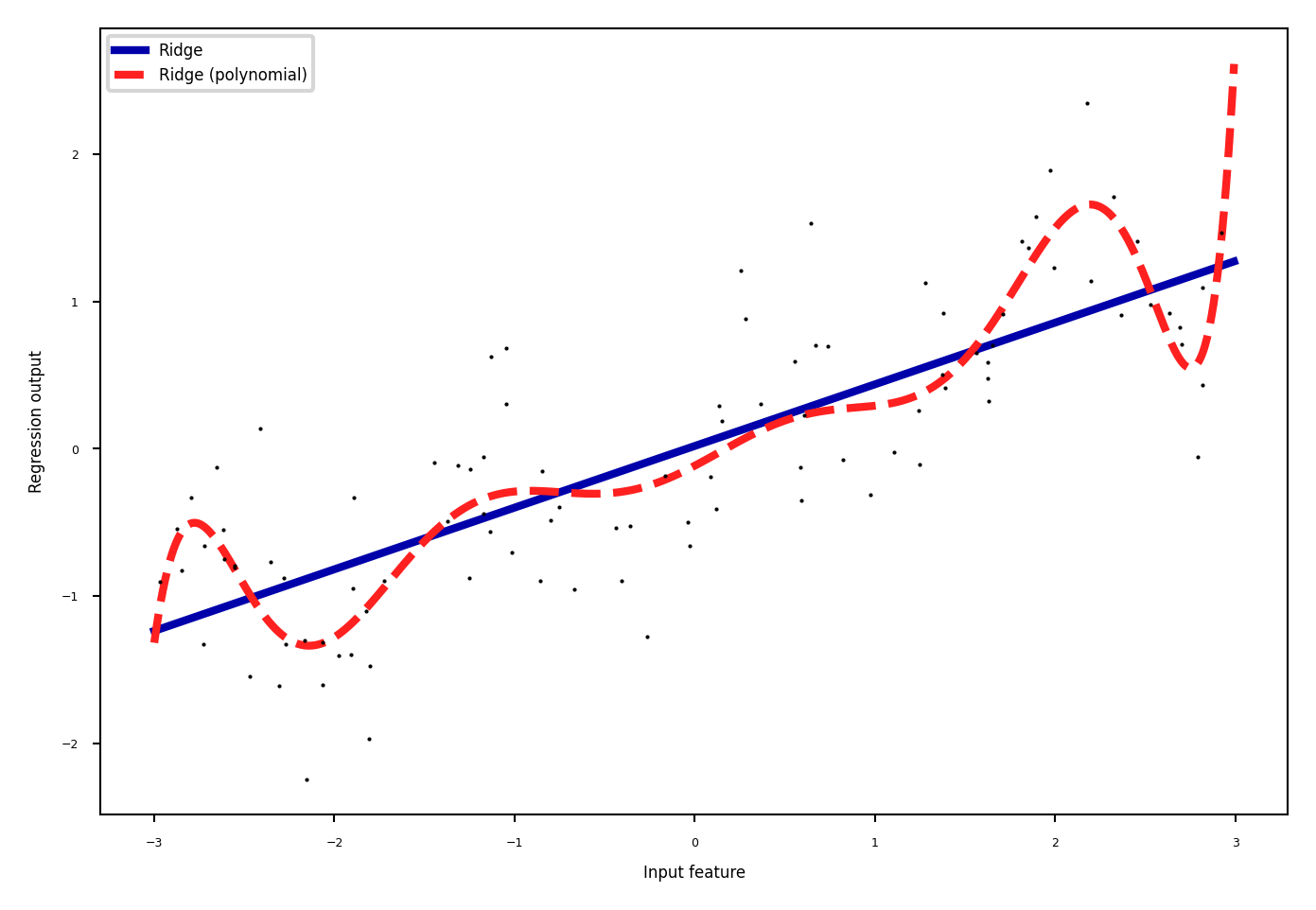
Polynomials#

Add all polynomials up to degree $d$ and all products
- Equivalent to polynomial basis expansions $$[1, x_1, ..., x_p] \xrightarrow{} [1, x_1, ..., x_p, x_1^2, ..., x_p^2, ..., x_p^d, x_1 x_2, ..., x_{p-1} x_p]$$

../_images/4980b5dc40605c06e122593d0a35104d0f084758e198a191734b4891620b8468.png

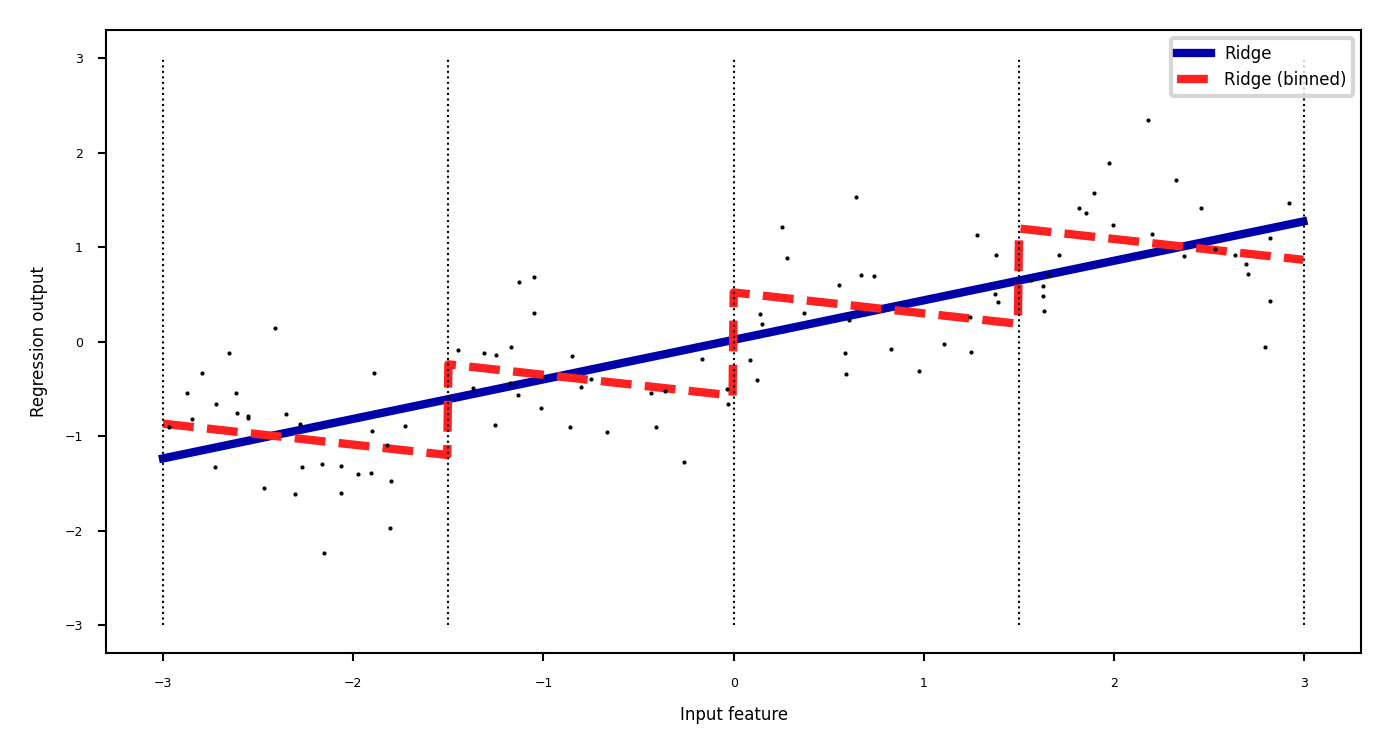
Binning#

Partition numeric feature values into $n$ intervals (bins)
Create $n$ new one-hot features, 1 if original value falls in corresponding bin
Models different intervals differently (e.g. different age groups)

table_font_size = 20
heading_properties = [('font-size', table_font_size)]
cell_properties = [('font-size', table_font_size)]
dfstyle = [dict(selector="th", props=heading_properties),\
 dict(selector="td", props=cell_properties)]

	orig	[-1.5,0.0]	[0.0,1.5]	[1.5,3.0]
0	-0.752759	1.000000	0.000000	0.000000
1	2.704286	0.000000	0.000000	1.000000
2	1.391964	0.000000	1.000000	0.000000

../_images/83c417b4c05b8f628a94022d6ca134f06373da7dc1cf61e0affbc902ac5b78f2.png

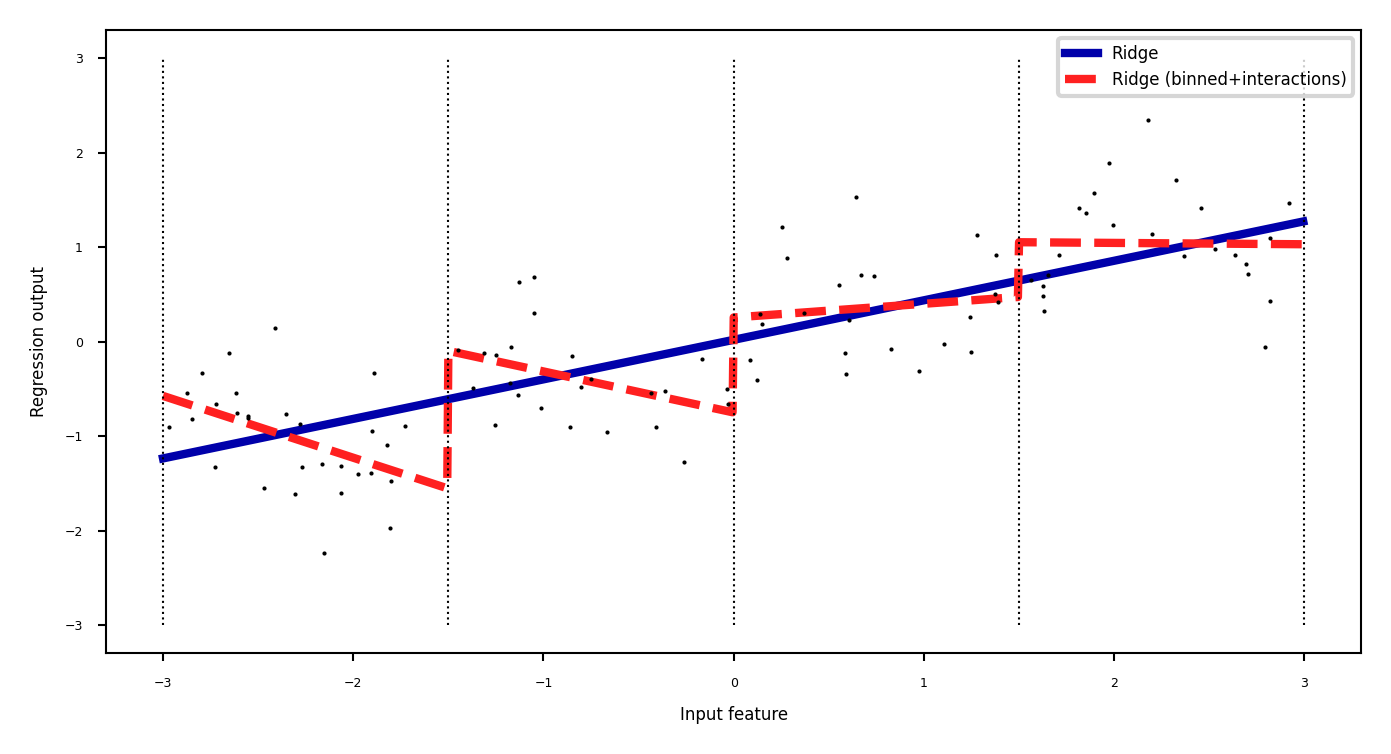
Binning + interaction features#

Add interaction features (or product features )
- Product of the bin encoding and the original feature value
- Learn different weights per bin

	orig	b1	b2	b3	X*b0	X*b1	X*b2	X*b3
0	-0.752759	1.000000	0.000000	0.000000	-0.000000	-0.752759	-0.000000	-0.000000
1	2.704286	0.000000	0.000000	1.000000	0.000000	0.000000	0.000000	2.704286
2	1.391964	0.000000	1.000000	0.000000	0.000000	0.000000	1.391964	0.000000

../_images/71389e536dcedbc7a1bdc24f7eb4e4ff0b59168752f6b22beb7d0f0b3b9d8f54.png

Categorical feature interactions#

One-hot-encode categorical feature
Multiply every one-hot-encoded column with every numeric feature
Allows to built different submodels for different categories

	gender	age	pageviews	time
0	M	14	70	269
1	F	16	12	1522
2	M	12	42	235
3	F	25	64	63
4	F	22	93	21

	age_M	pageviews_M	time_M	gender_M_M	age_F	pageviews_F	time_F	gender_F_F
0	14	70	269	True	0	0	0	False
1	0	0	0	False	16	12	1522	True
2	12	42	235	True	0	0	0	False
3	0	0	0	False	25	64	63	True
4	0	0	0	False	22	93	21	True

Summary#

Data preprocessing is a crucial part of machine learning
- Scaling is important for many distance-based methods (e.g. kNN, SVM, Neural Nets)
- Selecting features can speed up models and reduce overfitting
- Feature engineering is often useful for linear models
- Many more techniques (e.g. missing value imputation, handling data imbalance,…) will be discussed in the data preprocessing lecture
Pipelines allow us to encapsulate multiple steps in a convenient way
- Avoids data leakage, crucial for proper evaluation
Choose the right preprocessing steps and models in your pipeline
- Cross-validation helps, but the search space is huge
- Smarter techniques exist to automate this process (i.e. AutoML)