Basics of modeling, optimization, and regularization
Joaquin Vanschoren
Source
# Auto-setup when running on Google Colab
import os
if 'google.colab' in str(get_ipython()) and not os.path.exists('/content/master'):
!git clone -q https://github.com/ML-course/master.git /content/master
!pip --quiet install -r /content/master/requirements_colab.txt
%cd master/notebooks
# Global imports and settings
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
from preamble import *
interactive = True # Set to True for interactive plots
if interactive:
fig_scale = 0.3
plt.rcParams.update(print_config)
else: # For printing
fig_scale = 0.3
plt.rcParams.update(print_config)Notation and Definitions¶
A scalar is a simple numeric value, denoted by an italic letter:
A vector is a 1D ordered array of n scalars, denoted by a bold letter:
denotes the th element of a vector, thus .
Note: some other courses use notation
A set is an unordered collection of unique elements, denote by caligraphic capital:
A matrix is a 2D array of scalars, denoted by bold capital:
denotes the th row of the matrix
denotes the th column
denotes the element in the th row, th column, thus
, an matrix, can represent data points in a -dimensional space
Every row is a vector that can represent a point in an p-dimensional space, given a basis.
The standard basis for a Euclidean space is the set of unit vectors
E.g. if
Source
X = np.array([[3.24 , 1.2 ],[2.24, 0.2],[3.0 , 0.6 ]])
fig = plt.figure(figsize=(5*fig_scale,4*fig_scale))
plt.scatter(X[:,0],X[:,1]);
for i in range(3):
plt.annotate(i, (X[i,0]+0.02, X[i,1]))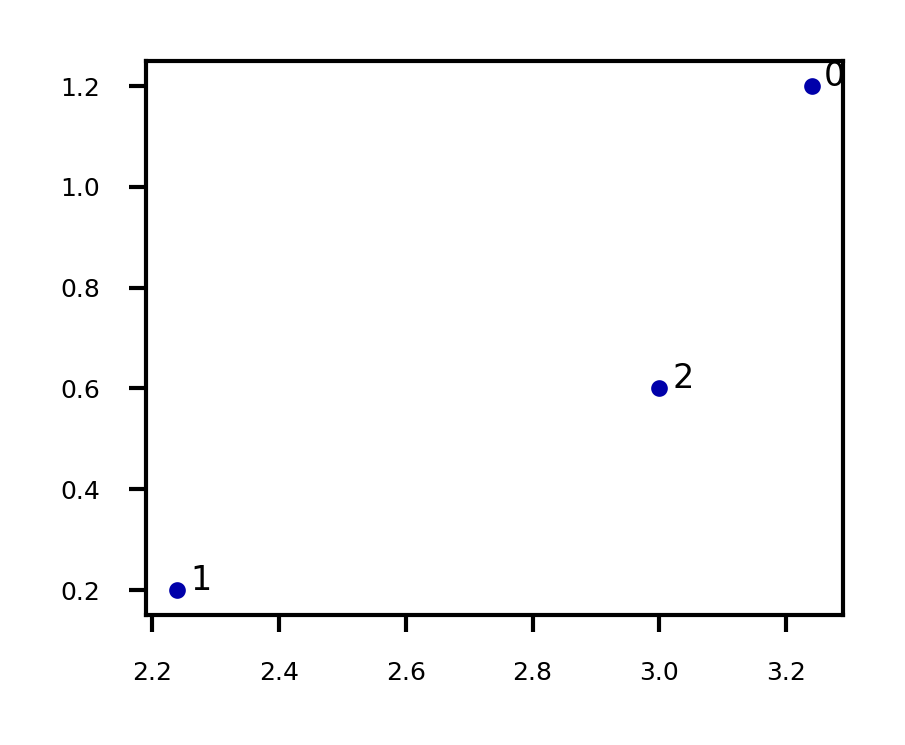
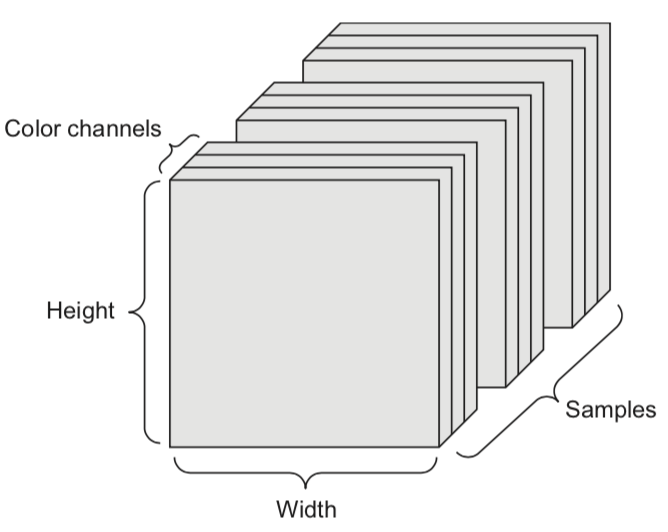
A tensor is an k-dimensional array of data, denoted by an italic capital:
k is also called the order, degree, or rank
denotes the element or sub-tensor in the corresponding position
A set of color images can be represented by:
a 4D tensor (sample x height x width x color channel)
a 2D tensor (sample x flattened vector of pixel values)
Basic operations¶
Sums and products are denoted by capital Sigma and capital Pi:
Operations on vectors are element-wise: e.g.
Dot product
Matrix product
A function relates an input element to an output
It has a local minimum at if in interval
It has a global minimum at if for any value for
A vector function consumes an input and produces a vector:
returns the largest value f(x) for any x
returns the element x that maximizes f(x)
Gradients¶
A derivative of a function describes how fast grows or decreases
The process of finding a derivative is called differentiation
Derivatives for basic functions are known
For non-basic functions we use the chain rule:
A function is differentiable if it has a derivative in any point of it’s domain
It’s continuously differentiable if is a continuous function
We say is smooth if it is infinitely differentiable, i.e., all exist
A gradient is the derivative of a function in multiple dimensions
It is a vector of partial derivatives:
E.g.
Example:
Evaluated at point (-4,1):
These are the slopes at point (-4,1) in the direction of and respectively
Source
from mpl_toolkits import mplot3d
import ipywidgets as widgets
from ipywidgets import interact, interact_manual
# f = -(x0^2 + x1^2)
def g_f(x0, x1):
return -(x0 ** 2 + x1 ** 2)
def g_dfx0(x0):
return -2 * x0
def g_dfx1(x1):
return -2 * x1
@interact
def plot_gradient(rotation=(0,240,10)):
# plot surface of f
fig = plt.figure(figsize=(12*fig_scale,5*fig_scale))
ax = plt.axes(projection="3d")
x0 = np.linspace(-6, 6, 30)
x1 = np.linspace(-6, 6, 30)
X0, X1 = np.meshgrid(x0, x1)
ax.plot_surface(X0, X1, g_f(X0, X1), rstride=1, cstride=1,
cmap='winter', edgecolor='none',alpha=0.3)
# choose point to evaluate: (-4,1)
i0 = -4
i1 = 1
iz = np.linspace(g_f(i0,i1), -82, 30)
ax.scatter3D(i0, i1, g_f(i0,i1), c="k", s=20*fig_scale,label='($i_0$,$i_1$) = (-4,1)')
ax.plot3D([i0]*30, [i1]*30, iz, linewidth=1*fig_scale, c='silver', linestyle='-')
ax.set_zlim(-80,0)
# plot intersects
ax.plot3D(x0,[1]*30,g_f(x0, 1),linewidth=3*fig_scale,alpha=0.9,label='$f(x_0,i_1)$',c='r',linestyle=':')
ax.plot3D([-4]*30,x1,g_f(-4, x1),linewidth=3*fig_scale,alpha=0.9,label='$f(i_0,x_1)$',c='b',linestyle=':')
# df/dx0 is slope of line at the intersect point
x0 = np.linspace(-8, 0, 30)
ax.plot3D(x0,[1]*30,g_dfx0(i0)*x0-g_f(i0,i1),linewidth=3*fig_scale,label=r'$\frac{\partial f}{\partial x_0}(i_0,i_1) x_0 + f(i_0,i_1)$',c='r',linestyle='-')
ax.plot3D([-4]*30,x1,g_dfx1(i1)*x1+g_f(i0,i1),linewidth=3*fig_scale,label=r'$\frac{\partial f}{\partial x_1}(i_0,i_1) x_1 + f(i_0,i_1)$',c='b',linestyle='-')
ax.set_xlabel('x0', labelpad=-4/fig_scale)
ax.set_ylabel('x1', labelpad=-4/fig_scale)
ax.get_zaxis().set_ticks([])
ax.view_init(30, rotation) # Use this to rotate the figure
ax.legend()
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.tick_params(axis='both', width=0, labelsize=10*fig_scale, pad=-6)
#plt.tight_layout()
plt.show()Source
if not interactive:
plot_gradient(rotation=120)Distributions and Probabilities¶
The normal (Gaussian) distribution with mean and standard deviation is noted as
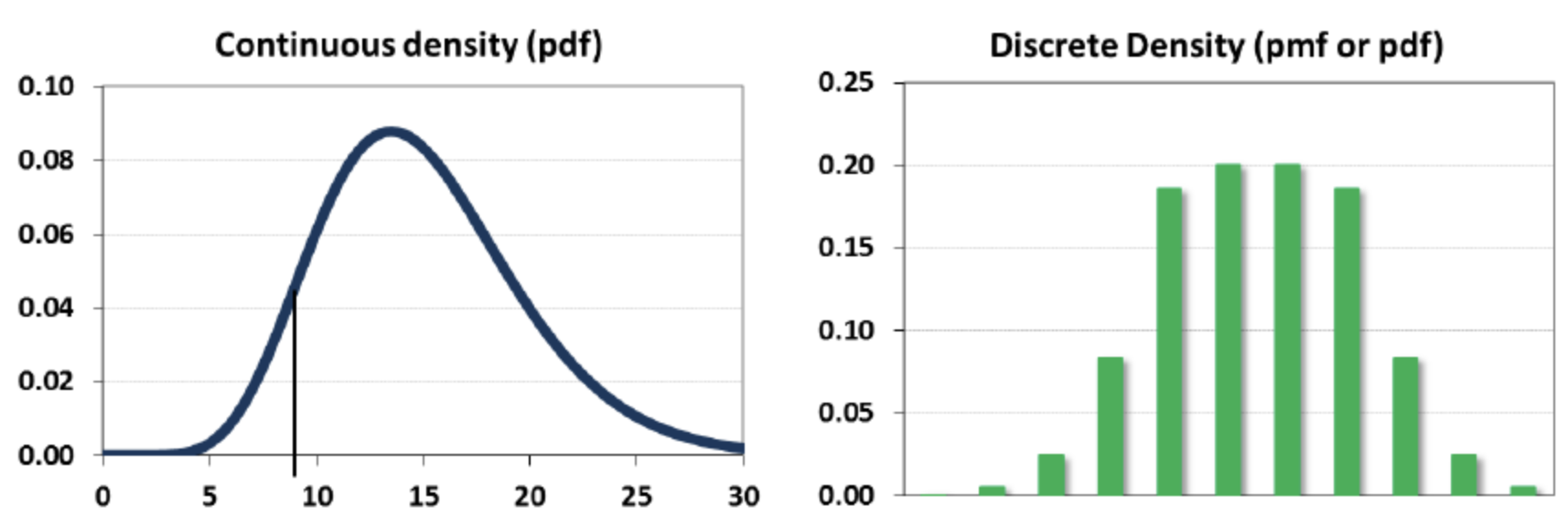
A random variable can be continuous or discrete
A probability distribution of a continuous variable : probability density function (pdf)
The expectation is given by
A probability distribution of a discrete variable: probability mass function (pmf)
The expectation (or mean)
Linear models¶
Linear models make a prediction using a linear function of the input features
Learn from , given a loss function :
Many algorithms with different : Least squares, Ridge, Lasso, Logistic Regression, Linear SVMs,...
Can be very powerful (and fast), especially for large datasets with many features.
Can be generalized to learn non-linear patterns: Generalized Linear Models
Features can be augmentented with polynomials of the original features
Features can be transformed according to a distribution (Poisson, Tweedie, Gamma,...)
Some linear models (e.g. SVMs) can be kernelized to learn non-linear functions
Linear models for regression¶
Prediction formula for input features x:
... usually called weights or coefficients , the bias or intercept
Assumes that errors are
Source
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from mglearn.datasets import make_wave
Xw, yw = make_wave(n_samples=60)
Xw_train, Xw_test, yw_train, yw_test = train_test_split(Xw, yw, random_state=42)
line = np.linspace(-3, 3, 100).reshape(-1, 1)
lr = LinearRegression().fit(Xw_train, yw_train)
print("w_1: %f w_0: %f" % (lr.coef_[0], lr.intercept_))
plt.figure(figsize=(6*fig_scale, 3*fig_scale))
plt.plot(line, lr.predict(line), lw=fig_scale)
plt.plot(Xw_train, yw_train, 'o', c='b')
#plt.plot(X_test, y_test, '.', c='r')
ax = plt.gca()
ax.grid(True)
ax.set_ylim(-2, 2)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(["model", "training data"], loc="best");w_1: 0.393906 w_0: -0.031804
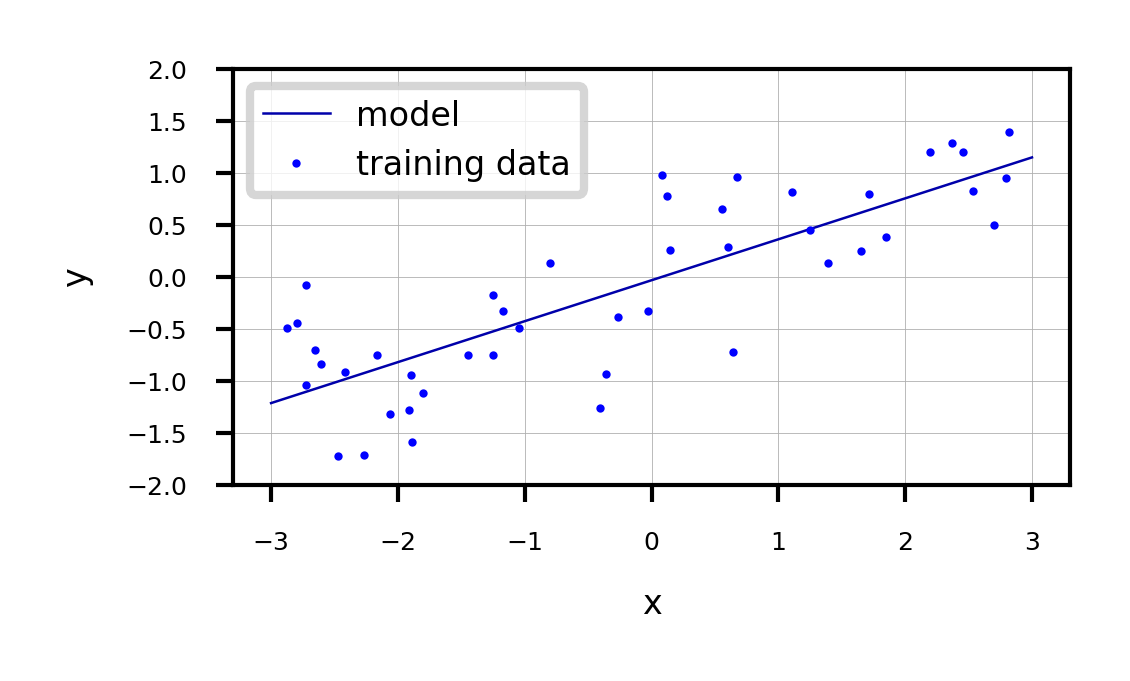
Linear Regression (aka Ordinary Least Squares)¶
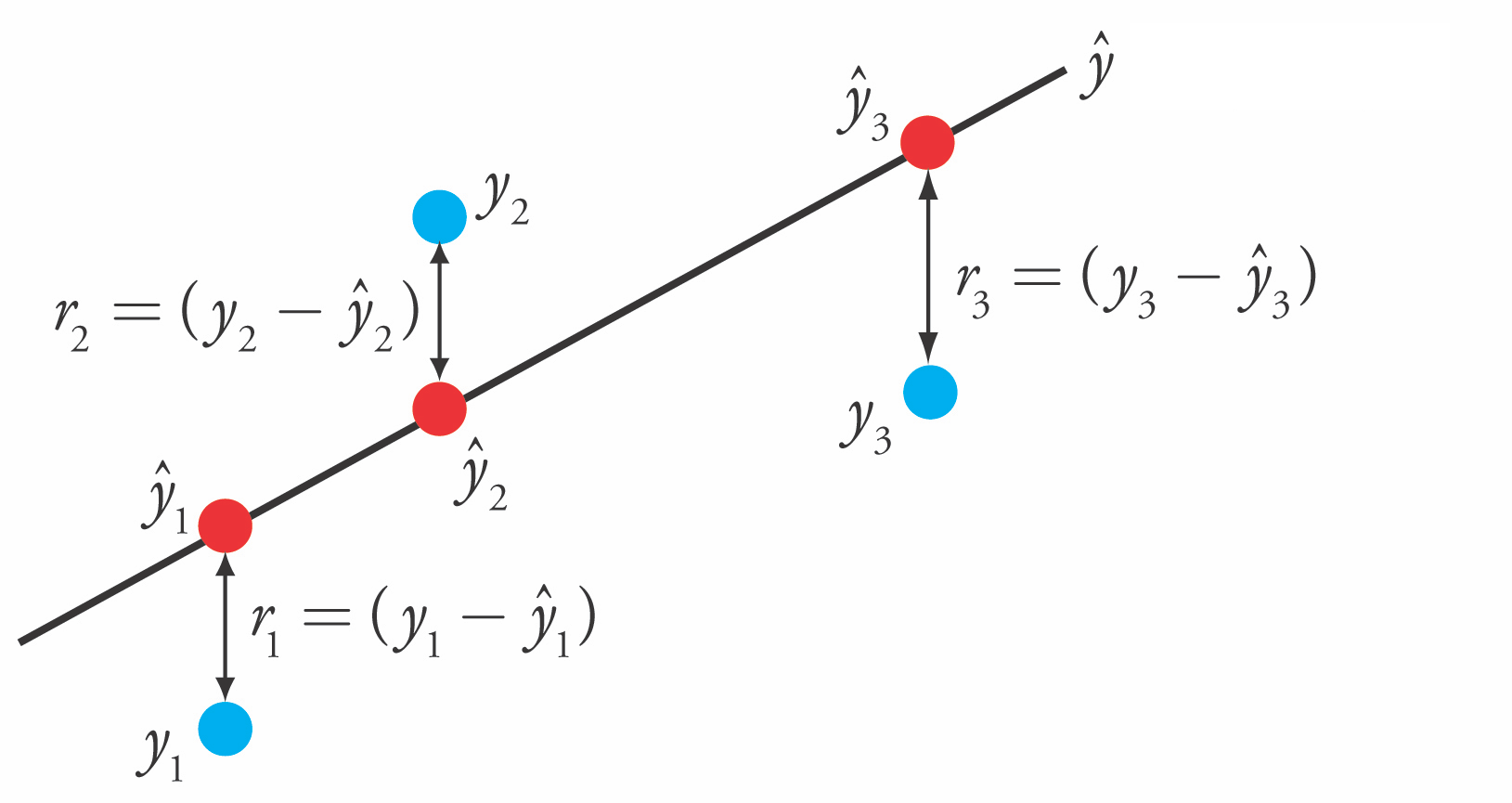
Loss function is the sum of squared errors (SSE) (or residuals) between predictions (red) and the true regression targets (blue) on the training set.
Solving ordinary least squares¶
Convex optimization problem with unique closed-form solution:
Add a column of 1’s to the front of X to get
Slow. Time complexity is quadratic in number of features:
X has rows, features, hence has dimensionality
Only works if
Gradient Descent
Faster for large and/or high-dimensional datasets
When cannot be computed or takes too long ( or is too large)
When you want more control over the learning process
Very easily overfits.
coefficients become very large (steep incline/decline)
small change in the input x results in a very different output y
No hyperparameters that control model complexity
Gradient Descent¶
Start with an initial, random set of weights:
Given a differentiable loss function (e.g. ), compute
For least squares:
If feature is associated with big errors, the gradient wrt will be large
Update all weights slightly (by step size or learning rate ) in ‘downhill’ direction.
Basic update rule (step s):
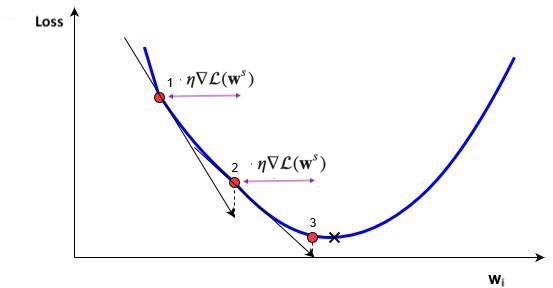
Important hyperparameters
Learning rate
Too small: slow convergence. Too large: possible divergence
Maximum number of iterations
Too small: no convergence. Too large: wastes resources
Learning rate decay with decay rate
E.g. exponential (), inverse-time (),...
Many more advanced ways to control learning rate (see later)
Adaptive techniques: depend on how much loss improved in previous step
Source
import math
# Some convex function to represent the loss
def l_fx(x):
return (x * 4)**2
# Derivative to compute the gradient
def l_dfx0(x0):
return 8 * x0
@interact
def plot_learning_rate(learn_rate=(0.01,0.4,0.01), exp_decay=False):
w = np.linspace(-1,1,101)
f = [l_fx(i) for i in w]
w_current = -0.75
learn_rate_current = learn_rate
fw = [] # weight values
fl = [] # loss values
for i in range(10):
fw.append(w_current)
fl.append(l_fx(w_current))
# Decay
if exp_decay:
learn_rate_current = learn_rate * math.exp(-0.3*i)
# Update rule
w_current = w_current - learn_rate_current * l_dfx0(w_current)
fig, ax = plt.subplots(figsize=(5*fig_scale,3*fig_scale))
ax.set_xlabel('w')
ax.set_xticks([])
ax.set_ylabel('loss')
ax.plot(w, f, lw=2*fig_scale, ls='-', c='k', label='Loss')
ax.plot(fw, fl, '--bo', lw=2*fig_scale, markersize=3)
plt.ylim(-1,16)
plt.xlim(-1,1)
plt.show()
Source
if not interactive:
plot_learning_rate(learn_rate=0.21, exp_decay=False)import torch
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
from ipywidgets import interact, interactive
# 1. Setup Device (GPU if available)
if torch.cuda.is_available(): # For CUDA based systems
device = torch.device("cuda")
if torch.backends.mps.is_available(): # For MPS (M1-M4 Mac) based systems
device = torch.device("mps")
# print(f"Used device: {device}")
# Toy surface (Beale function)
def f(x, y):
return (1.5 - x + x*y)**2 + (2.25 - x + x*y**2)**2 + (2.625 - x + x*y**3)**2
opt_names = ['sgd', 'sgd_decay']
cmap = plt.cm.get_cmap('tab10')
colors = [cmap(x/10) for x in range(10)]
# --- Training Loop 1: Compare Optimizers ---
all_paths = []
for name in opt_names:
# Initialize variables on GPU
x = torch.tensor(0.8, device=device, requires_grad=True)
y = torch.tensor(1.6, device=device, requires_grad=True)
# Initialize Optimizer
# Note: PyTorch optimizers need the parameters passed at creation.
lr = 0.01
if name == 'sgd':
opt = torch.optim.SGD([x, y], lr=lr)
scheduler = None
elif name == 'sgd_decay':
opt = torch.optim.SGD([x, y], lr=0.02)
# Emulate TF ExponentialDecay: decay_rate^(step/decay_steps).
# For per-step updates, gamma = decay_rate^(1/decay_steps)
gamma = 0.96**(1/100)
scheduler = torch.optim.lr_scheduler.ExponentialLR(opt, gamma=gamma)
x_history = []
y_history = []
z_prev = 0.0
max_steps = 100
for step in range(max_steps):
# 1. Forward pass
z = f(x, y)
# 2. Record history (Move to CPU/Numpy)
x_history.append(x.detach().cpu().item())
y_history.append(y.detach().cpu().item())
# Check convergence
if np.abs(z_prev - z.detach().cpu().item()) < 1e-6:
break
z_prev = z.detach().cpu().item()
# 3. Backward pass and Optimization
opt.zero_grad() # Clear previous gradients
z.backward() # Compute gradients
opt.step() # Update parameters
if scheduler:
scheduler.step()
# Process path for plotting
x_history = np.array(x_history)
y_history = np.array(y_history)
path = np.concatenate((np.expand_dims(x_history, 1), np.expand_dims(y_history, 1)), axis=1).T
all_paths.append(path)
# --- Plotting Setup ---
# (Calculations done on CPU for easier Matplotlib integration)
number_of_points = 50
minima = np.array([3., .5])
x_min, x_max = -2, 3.5
y_min, y_max = -3.5, 2
x_points = np.linspace(x_min, x_max, number_of_points)
y_points = np.linspace(y_min, y_max, number_of_points)
x_mesh, y_mesh = np.meshgrid(x_points, y_points)
# Calculate Z mesh (pure numpy is sufficient for grid generation)
z_grid = np.array([f(xps, yps) for xps, yps in zip(x_mesh, y_mesh)])
def plot_optimizers(ax, iterations, optimizers_to_show):
ax.contour(x_mesh, y_mesh, z_grid, levels=np.logspace(-0.5, 5, 25), norm=LogNorm(), cmap=plt.cm.jet, linewidths=fig_scale, zorder=-1)
ax.plot(*minima, 'r*', markersize=20*fig_scale)
for name, path, color in zip(opt_names, all_paths, colors):
if name in optimizers_to_show:
p = path[:, :iterations]
if p.shape[1] > 0: # Ensure we have data
ax.plot([], [], color=color, label=name, lw=3*fig_scale, linestyle='-')
if p.shape[1] > 1:
ax.quiver(p[0,:-1], p[1,:-1], p[0,1:]-p[0,:-1], p[1,1:]-p[1,:-1], scale_units='xy', angles='xy', scale=1, color=color, lw=4)
ax.set_xlim((x_min, x_max))
ax.set_ylim((y_min, y_max))
ax.legend(loc='lower left', prop={'size': 15*fig_scale})
ax.set_xticks([])
ax.set_yticks([])
plt.tight_layout()
# --- Training Loop 2: Learning Rate Sweep ---
all_lr_paths = []
lr_range = [0.005 * i for i in range(1, 11)] # Adjusted range slightly to avoid 0.0
for lr in lr_range:
# Re-init variables on GPU
x = torch.tensor(0.8, device=device, requires_grad=True)
y = torch.tensor(1.6, device=device, requires_grad=True)
# Init Optimizer
opt = torch.optim.SGD([x, y], lr=lr)
x_history = []
y_history = []
z_prev = 0.0
max_steps = 100
for step in range(max_steps):
z = f(x, y)
x_history.append(x.detach().cpu().item())
y_history.append(y.detach().cpu().item())
if np.abs(z_prev - z.detach().cpu().item()) < 1e-6:
break
z_prev = z.detach().cpu().item()
opt.zero_grad()
z.backward()
opt.step()
x_history = np.array(x_history)
y_history = np.array(y_history)
path = np.vstack((x_history, y_history))
all_lr_paths.append(path)
# --- Plotting LR Sweep ---
def plot_learning_rate_optimizers(ax, iterations, lr):
ax.contour(x_mesh, y_mesh, z_grid, levels=np.logspace(-0.5, 5, 25), norm=LogNorm(), cmap=plt.cm.jet, linewidths=1, zorder=-1)
ax.plot(*minima, 'r*', markersize=20)
for path, lrate in zip(all_lr_paths, lr_range):
# Comparison with tolerance for float equality
if abs(lrate - lr) < 1e-5:
p = path[:, :iterations]
if p.shape[1] > 0:
ax.plot([], [], color='b', label=f"Learning rate {round(lr, 3)}", lw=3, linestyle='-')
if p.shape[1] > 1:
ax.quiver(p[0, :-1], p[1, :-1], p[0, 1:] - p[0, :-1], p[1, 1:] - p[1, :-1], scale_units='xy', angles='xy', scale=1, color='b', lw=4)
ax.set_xlim((x_min, x_max))
ax.set_ylim((y_min, y_max))
ax.legend(loc='lower left', prop={'size': 6})
ax.set_xticks([])
ax.set_yticks([])
plt.tight_layout()Effect of learning rate
Source
@interact
def plot_lr(iterations=(1, 100, 1), learning_rate=(0.005, 0.045, 0.005)): # Fixed range
fig, ax = plt.subplots(figsize=(6 * fig_scale, 4 * fig_scale))
plot_learning_rate_optimizers(ax, iterations, learning_rate)
plt.show()
if not interactive:
plot_lr(iterations=50, learning_rate=0.02)Effect of learning rate decay
Source
@interact
def compare_optimizers(iterations=(1,100,1), optimizer1=opt_names, optimizer2=opt_names):
fig, ax = plt.subplots(figsize=(6*fig_scale,4*fig_scale))
plot_optimizers(ax,iterations,[optimizer1,optimizer2])
plt.show()
if not interactive:
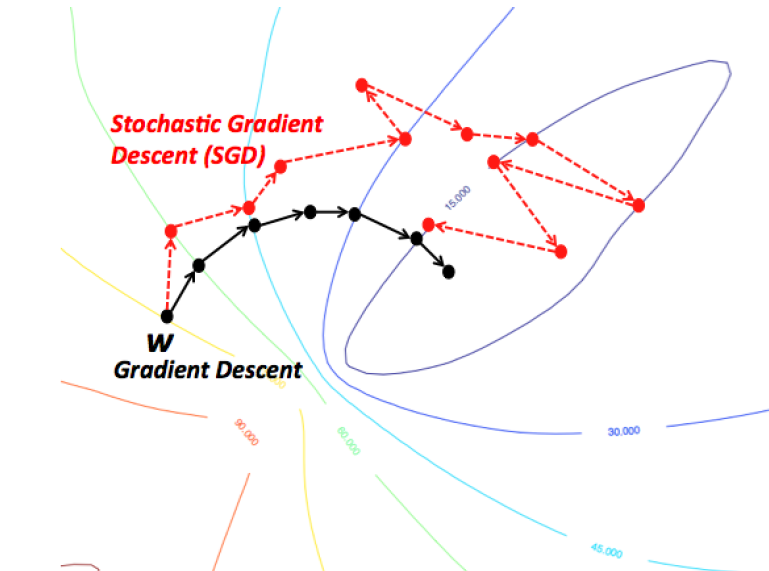
compare_optimizers(iterations=50, optimizer1="sgd", optimizer2="sgd_decay")In two dimensions:
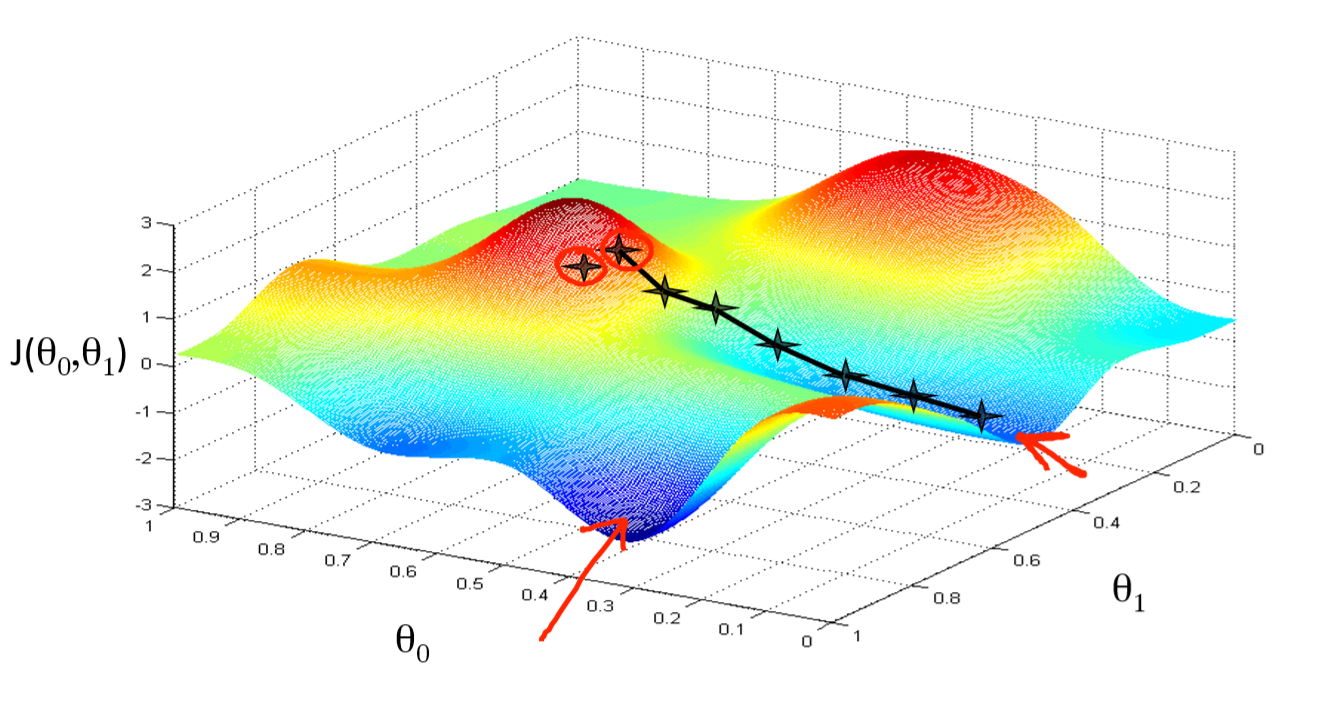
You can get stuck in local minima (if the loss is not fully convex)
If you have many model parameters, this is less likely
You always find a way down in some direction
Models with many parameters typically find good local minima
Intuition: walking downhill using only the slope you “feel” nearby

(Image by A. Karpathy)
Stochastic Gradient Descent (SGD)¶
Compute gradients not on the entire dataset, but on a single data point at a time
Gradient descent:
Stochastic Gradient Descent:
Many smoother variants, e.g.
In practice¶
Linear regression can be found in
sklearn.linear_model. We’ll evaluate it on the Boston Housing dataset.LinearRegressionuses closed form solution,SGDRegressorwithloss='squared_loss'uses Stochastic Gradient DescentLarge coefficients signal overfitting
Test score is much lower than training score
from sklearn.linear_model import LinearRegression
lr = LinearRegression().fit(X_train, y_train)Source
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X_B, y_B = mglearn.datasets.load_extended_boston()
X_B_train, X_B_test, y_B_train, y_B_test = train_test_split(X_B, y_B, random_state=0)
lr = LinearRegression().fit(X_B_train, y_B_train)Source
print("Weights (coefficients): {}".format(lr.coef_[0:40]))
print("Bias (intercept): {}".format(lr.intercept_))Weights (coefficients): [ -412.711 -52.243 -131.899 -12.004 -15.511 28.716 54.704
-49.535 26.582 37.062 -11.828 -18.058 -19.525 12.203
2980.781 1500.843 114.187 -16.97 40.961 -24.264 57.616
1278.121 -2239.869 222.825 -2.182 42.996 -13.398 -19.389
-2.575 -81.013 9.66 4.914 -0.812 -7.647 33.784
-11.446 68.508 -17.375 42.813 1.14 ]
Bias (intercept): 30.93456367364383
Source
print("Training set score (R^2): {:.2f}".format(lr.score(X_B_train, y_B_train)))
print("Test set score (R^2): {:.2f}".format(lr.score(X_B_test, y_B_test)))Training set score (R^2): 0.95
Test set score (R^2): 0.61
Ridge regression¶
Adds a penalty term to the least squares loss function:
Model is penalized if it uses large coefficients ()
Each feature should have as little effect on the outcome as possible
We don’t want to penalize , so we leave it out
Regularization: explicitly restrict a model to avoid overfitting.
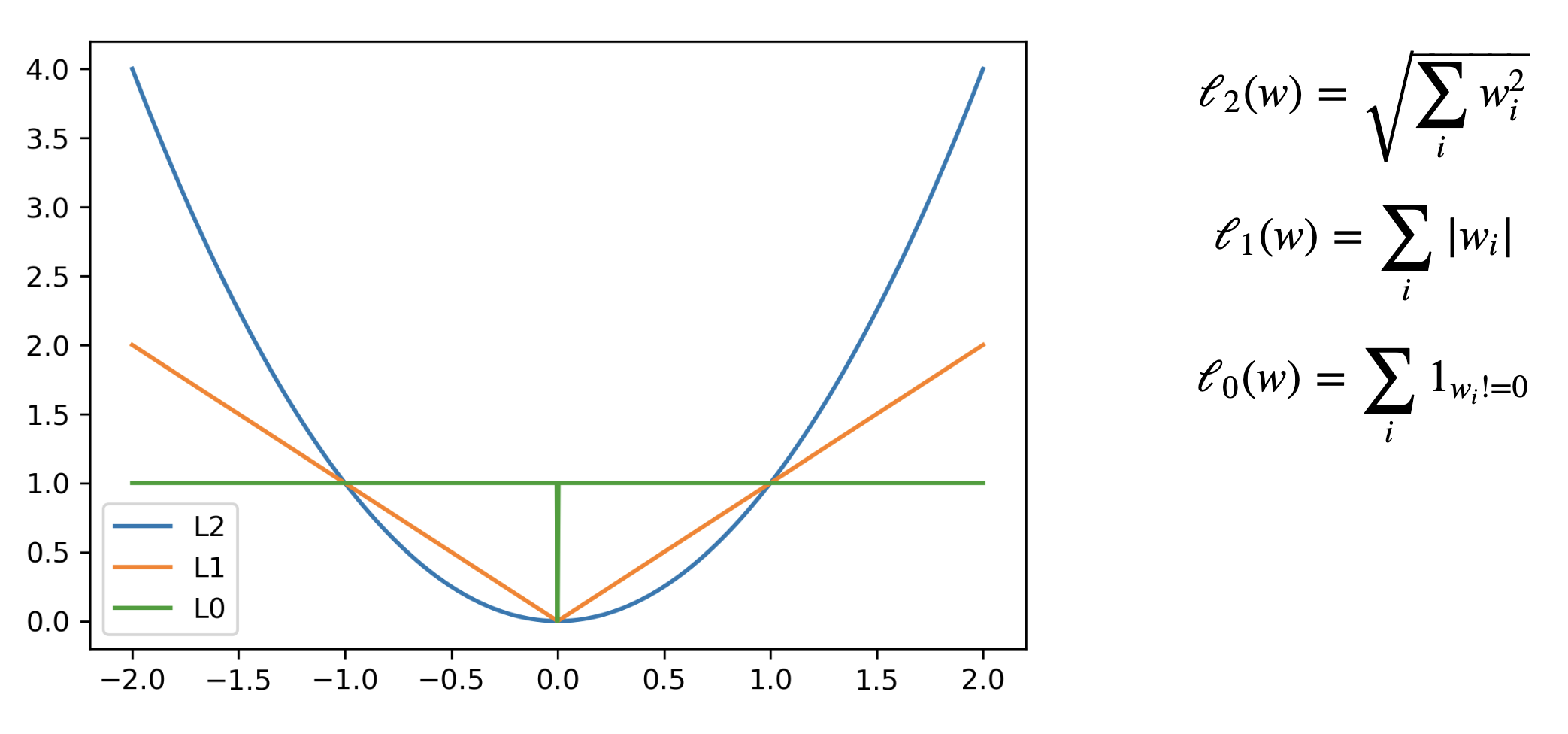
Called L2 regularization because it uses the L2 norm:
The strength of the regularization can be controlled with the hyperparameter.
Increasing causes more regularization (or shrinkage). Default is 1.0.
Still convex. Can be optimized in different ways:
Closed form solution (a.k.a. Cholesky):
Gradient descent and variants, e.g. Stochastic Average Gradient (SAG,SAGA)
Conjugate gradient (CG): each new gradient is influenced by previous ones
Use Cholesky for smaller datasets, Gradient descent for larger ones
In practice¶
from sklearn.linear_model import Ridge
lr = Ridge().fit(X_train, y_train)Source
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_B_train, y_B_train)
print("Weights (coefficients): {}".format(ridge.coef_[0:40]))
print("Bias (intercept): {}".format(ridge.intercept_))
print("Training set score: {:.2f}".format(ridge.score(X_B_train, y_B_train)))
print("Test set score: {:.2f}".format(ridge.score(X_B_test, y_B_test)))Weights (coefficients): [-1.414 -1.557 -1.465 -0.127 -0.079 8.332 0.255 -4.941 3.899 -1.059
-1.584 1.051 -4.012 0.334 0.004 -0.849 0.745 -1.431 -1.63 -1.405
-0.045 -1.746 -1.467 -1.332 -1.692 -0.506 2.622 -2.092 0.195 -0.275
5.113 -1.671 -0.098 0.634 -0.61 0.04 -1.277 -2.913 3.395 0.792]
Bias (intercept): 21.390525958609953
Training set score: 0.89
Test set score: 0.75
Test set score is higher and training set score lower: less overfitting!
We can plot the weight values for differents levels of regularization to explore the effect of .
Increasing regularization decreases the values of the coefficients, but never to 0.
Source
from __future__ import print_function
import ipywidgets as widgets
from ipywidgets import interact, interact_manual
from sklearn.linear_model import Ridge
@interact
def plot_ridge(alpha=(0,10.0,0.05)):
r = Ridge(alpha=alpha).fit(X_B_train, y_B_train)
fig, ax = plt.subplots(figsize=(8*fig_scale,1.5*fig_scale))
ax.plot(r.coef_, 'o', markersize=3)
ax.set_title("alpha {}, test score {:.2f} (training score {:.2f})".format(alpha, r.score(X_B_test, y_B_test), r.score(X_B_train, y_B_train)))
ax.set_xlabel("Coefficient index")
ax.set_ylabel("Coefficient magnitude")
ax.hlines(0, 0, len(r.coef_))
ax.set_ylim(-25, 25)
ax.set_xlim(0, 50);
plt.show()Source
if not interactive:
for alpha in [0.1, 10]:
plot_ridge(alpha)When we plot the train and test scores for every value, we see a sweet spot around
Models with smaller are overfitting
Models with larger are underfitting
Source
alpha=np.logspace(-3,2,num=20)
ai = list(range(len(alpha)))
test_score=[]
train_score=[]
for a in alpha:
r = Ridge(alpha=a).fit(X_B_train, y_B_train)
test_score.append(r.score(X_B_test, y_B_test))
train_score.append(r.score(X_B_train, y_B_train))
fig, ax = plt.subplots(figsize=(6*fig_scale,4*fig_scale))
ax.set_xticks(range(20))
ax.set_xticklabels(np.round(alpha,3))
ax.set_xlabel('alpha')
ax.plot(test_score, lw=2*fig_scale, label='test score')
ax.plot(train_score, lw=2*fig_scale, label='train score')
ax.legend()
plt.xticks(rotation=45);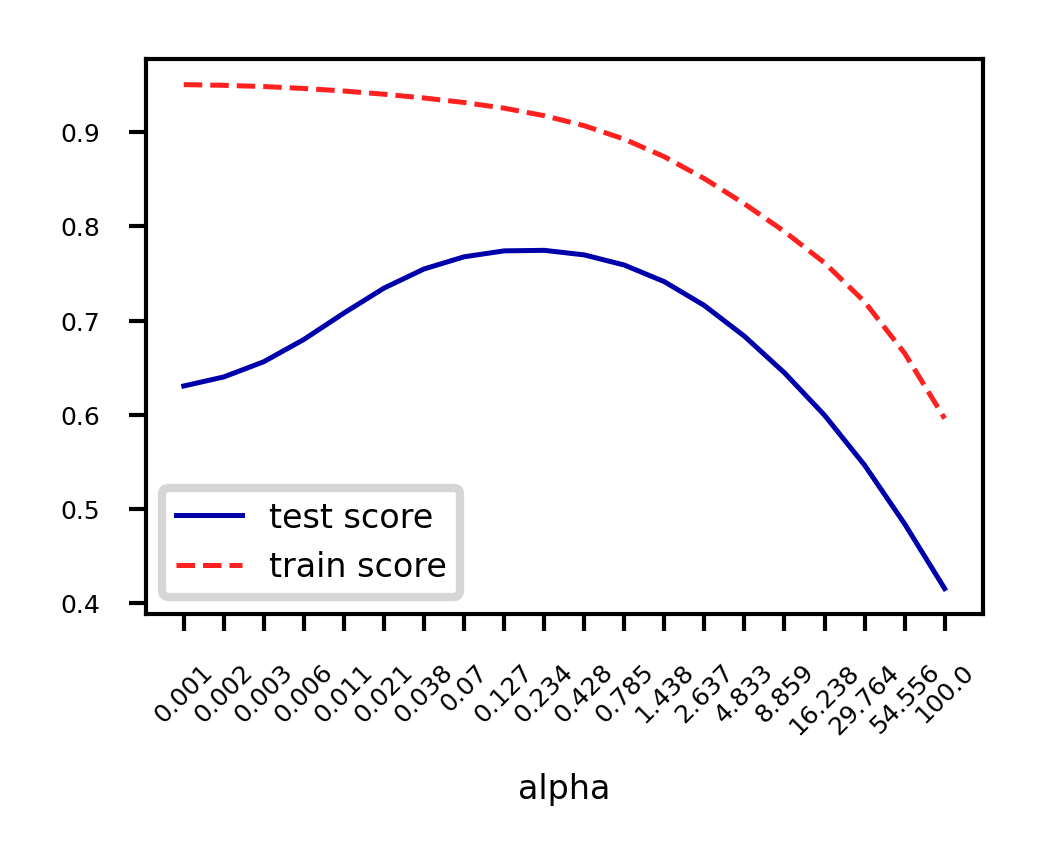
Other ways to reduce overfitting¶
Add more training data: with enough training data, regularization becomes less important
Ridge and ordinary least squares will have the same performance
Use fewer features: remove unimportant ones or find a low-dimensional embedding (e.g. PCA)
Fewer coefficients to learn, reduces the flexibility of the model
Scaling the data typically helps (and changes the optimal value)
Source
fig, ax = plt.subplots(figsize=(10*fig_scale,4*fig_scale))
mglearn.plots.plot_ridge_n_samples(ax)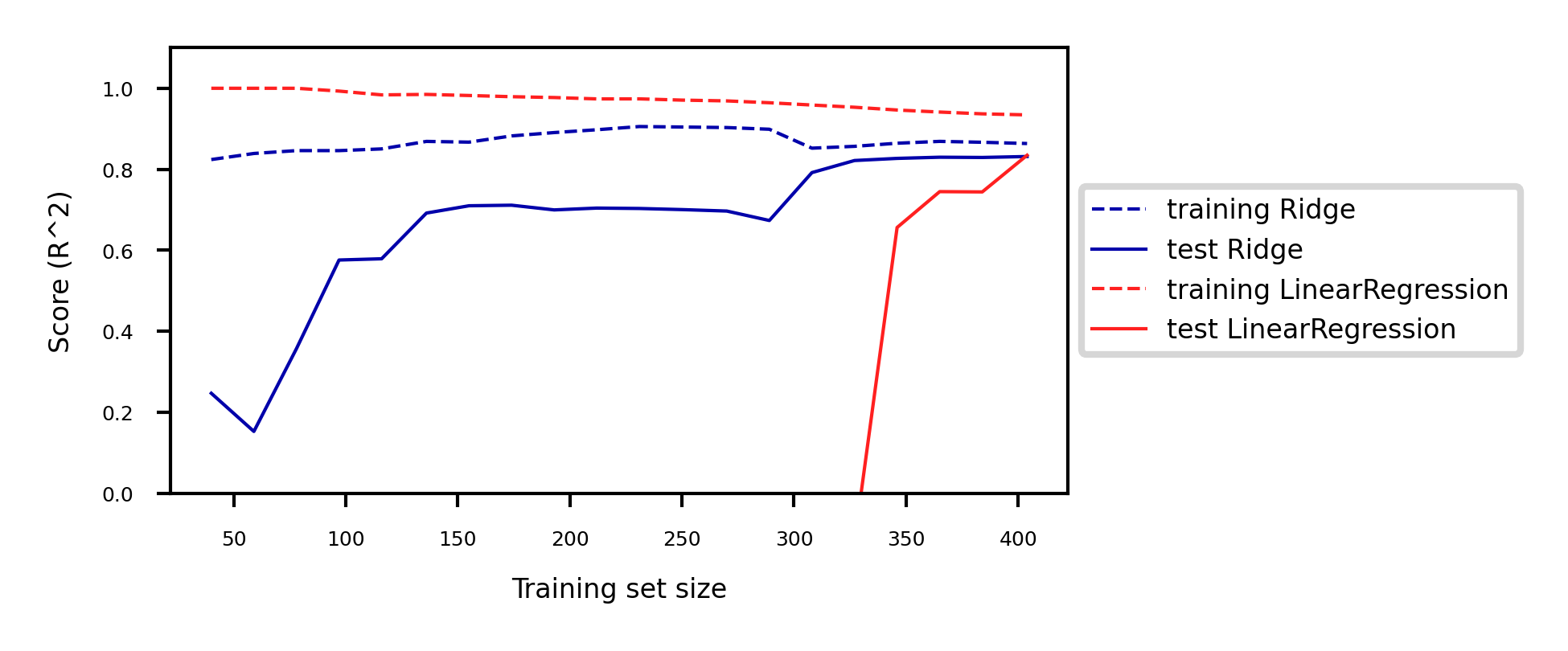
Lasso (Least Absolute Shrinkage and Selection Operator)¶
Adds a different penalty term to the least squares sum:
Called L1 regularization because it uses the L1 norm
Will cause many weights to be exactly 0
Same parameter to control the strength of regularization.
Will again have a ‘sweet spot’ depending on the data
No closed-form solution
Convex, but no longer strictly convex, and not differentiable
Weights can be optimized using coordinate descent
Analyze what happens to the weights:
L1 prefers coefficients to be exactly zero (sparse models)
Some features are ignored entirely: automatic feature selection
How can we explain this?
Source
from sklearn.linear_model import Lasso
@interact
def plot_lasso(alpha=(0,0.5,0.005)):
r = Lasso(alpha=alpha).fit(X_B_train, y_B_train)
fig, ax = plt.subplots(figsize=(8*fig_scale,1.5*fig_scale))
ax.plot(r.coef_, 'o', markersize=6*fig_scale)
ax.set_title("alpha {}, score {:.2f} (training score {:.2f})".format(alpha, r.score(X_B_test, y_B_test), r.score(X_B_train, y_B_train)), pad=0.5)
ax.set_xlabel("Coefficient index", labelpad=0)
ax.set_ylabel("Coefficient magnitude")
ax.hlines(0, 0, len(r.coef_))
ax.set_ylim(-25, 25);
ax.set_xlim(0, 50);
plt.show()Source
if not interactive:
for alpha in [0.00001, 0.01]:
plot_lasso(alpha)Coordinate descent¶
Alternative for gradient descent, supports non-differentiable convex loss functions (e.g. )
In every iteration, optimize a single coordinate (find minimum in direction of )
Continue with another coordinate, using a selection rule (e.g. round robin)
Faster iterations. No need to choose a step size (learning rate).
May converge more slowly. Can’t be parallellized.
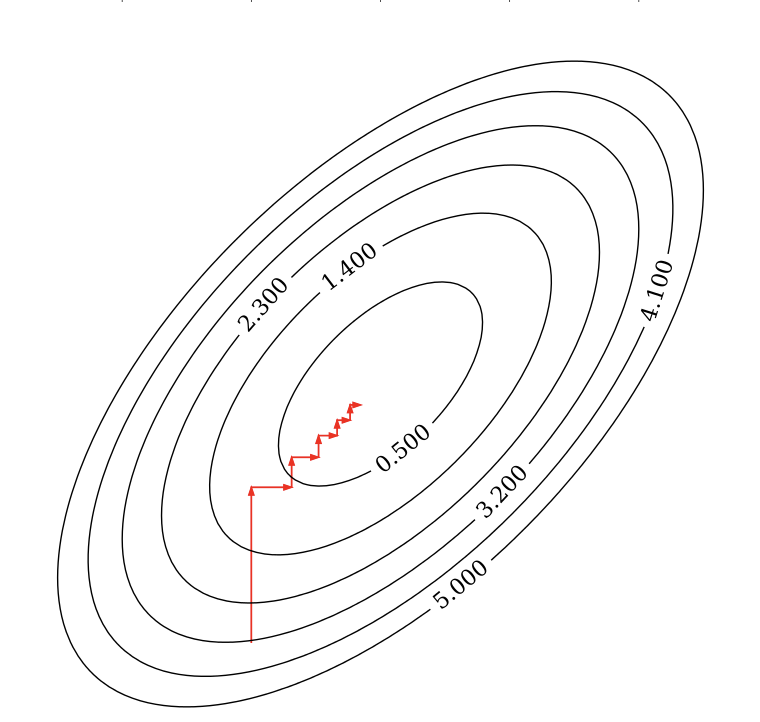
Coordinate descent with Lasso¶
Remember that
For one :
The L1 term is not differentiable but convex: we can compute the subgradient
Unique at points where is differentiable, a range of all possible slopes [a,b] where it is not
For , the subgradient =
Subdifferential if and are both convex
To find the optimum for Lasso , solve
In which is the part of excluding (assume for now)
can be seen as the ‘solution’: if
We found:
The Lasso solution has the form of a soft thresholding function
Small weights (all weights between and ) become 0: sparseness!
If the data is not normalized, with constant
Ridge solution: , thus
Source
@interact
def plot_rho(alpha=(0,2.0,0.05)):
w = np.linspace(-2,2,101)
r = w/(1+2*alpha)
l = [x+alpha if x <= -alpha else (x-alpha if x > alpha else 0) for x in w]
fig, ax = plt.subplots(figsize=(6*fig_scale,3*fig_scale))
ax.set_xlabel(r'$\rho$')
ax.set_ylabel(r'$w^{*}$')
ax.plot(w, w, lw=2*fig_scale, c='g', label='Ordinary Least Squares (SSE)')
ax.plot(w, r, lw=2*fig_scale, c='b', label='Ridge with alpha={}'.format(alpha))
ax.plot(w, l, lw=2*fig_scale, c='r', label='Lasso with alpha={}'.format(alpha))
ax.legend()
plt.grid()
plt.show()Source
if not interactive:
plot_rho(alpha=1)Least Squares Loss + L1 or L2
The Lasso curve has 3 parts (,,) corresponding to the thresholding function
For any minimum of least squares, L2 will be smaller, and L1 is more likely be exactly 0
Source
def c_fx(x):
fX = ((x * 2 - 1)**2) # Some convex function to represent the loss
return fX/9 # Scaling
def c_fl2(x,alpha):
return c_fx(x) + alpha * x**2
def c_fl1(x,alpha):
return c_fx(x) + alpha * abs(x)
def l2(x,alpha):
return alpha * x**2
def l1(x,alpha):
return alpha * abs(x)
@interact
def plot_losses(alpha=(0,1.0,0.05)):
w = np.linspace(-1,1,101)
f = [c_fx(i) for i in w]
r = [c_fl2(i,alpha) for i in w]
l = [c_fl1(i,alpha) for i in w]
rp = [l2(i,alpha) for i in w]
lp = [l1(i,alpha) for i in w]
fig, ax = plt.subplots(figsize=(8*fig_scale,4*fig_scale))
ax.set_xlabel('w')
ax.set_ylabel('loss')
ax.plot(w, rp, lw=1.5*fig_scale, ls=':', c='b', label='L2 with alpha={}'.format(alpha))
ax.plot(w, lp, lw=1.5*fig_scale, ls=':', c='r', label='L1 with alpha={}'.format(alpha))
ax.plot(w, f, lw=2*fig_scale, ls='-', c='k', label='Least Squares loss')
ax.plot(w, r, lw=2*fig_scale, ls='-', c='b', label='Loss + L2 (Ridge)'.format(alpha))
ax.plot(w, l, lw=2*fig_scale, ls='-', c='r', label='Loss + L1 (Lasso)'.format(alpha))
opt_f = np.argmin(f)
ax.scatter(w[opt_f], f[opt_f], c="k", s=50*fig_scale)
opt_r = np.argmin(r)
ax.scatter(w[opt_r], r[opt_r], c="b", s=50*fig_scale)
opt_l = np.argmin(l)
ax.scatter(w[opt_l], l[opt_l], c="r", s=50*fig_scale)
ax.legend()
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.ylim(-0.1,1)
plt.grid()
plt.show()Source
if not interactive:
plot_losses(alpha=0.5)In 2D (for 2 model weights and )
The least squared loss is a 2D convex function in this space (ellipses on the right)
For illustration, assume that L1 loss = L2 loss = 1
L1 loss (): the optimal {} (blue dot) falls on the diamond
L2 loss (): the optimal {} (cyan dot) falls on the circle
For L1, the loss is minimized if or is 0 (rarely so for L2)
Source
def plot_loss_interpretation():
line = np.linspace(-1.5, 1.5, 1001)
xx, yy = np.meshgrid(line, line)
l2 = xx ** 2 + yy ** 2
l1 = np.abs(xx) + np.abs(yy)
rho = 0.7
elastic_net = rho * l1 + (1 - rho) * l2
plt.figure(figsize=(5*fig_scale, 4*fig_scale))
ax = plt.gca()
elastic_net_contour = plt.contour(xx, yy, elastic_net, levels=[1], linewidths=2*fig_scale, colors="darkorange")
l2_contour = plt.contour(xx, yy, l2, levels=[1], linewidths=2*fig_scale, colors="c")
l1_contour = plt.contour(xx, yy, l1, levels=[1], linewidths=2*fig_scale, colors="navy")
ax.set_aspect("equal")
ax.spines['left'].set_position('center')
ax.spines['right'].set_color('none')
ax.spines['bottom'].set_position('center')
ax.spines['top'].set_color('none')
plt.clabel(elastic_net_contour, inline=1, fontsize=12*fig_scale,
fmt={1.0: 'elastic-net'}, manual=[(-0.6, -0.6)])
plt.clabel(l2_contour, inline=1, fontsize=12*fig_scale,
fmt={1.0: 'L2'}, manual=[(-0.5, -0.5)])
plt.clabel(l1_contour, inline=1, fontsize=12*fig_scale,
fmt={1.0: 'L1'}, manual=[(-0.5, -0.5)])
x1 = np.linspace(0.5, 1.5, 100)
x2 = np.linspace(-1.0, 1.5, 100)
X1, X2 = np.meshgrid(x1, x2)
Y = np.sqrt(np.square(X1/2-0.7) + np.square(X2/4-0.28))
cp = plt.contour(X1, X2, Y)
plt.clabel(cp, inline=1, fontsize=3)
ax.tick_params(axis='both', pad=0)
ax.scatter(1, 0, c="navy", s=50*fig_scale)
ax.scatter(0.89, 0.42, c="c", s=50*fig_scale)
plt.tight_layout()
plt.show()
plot_loss_interpretation()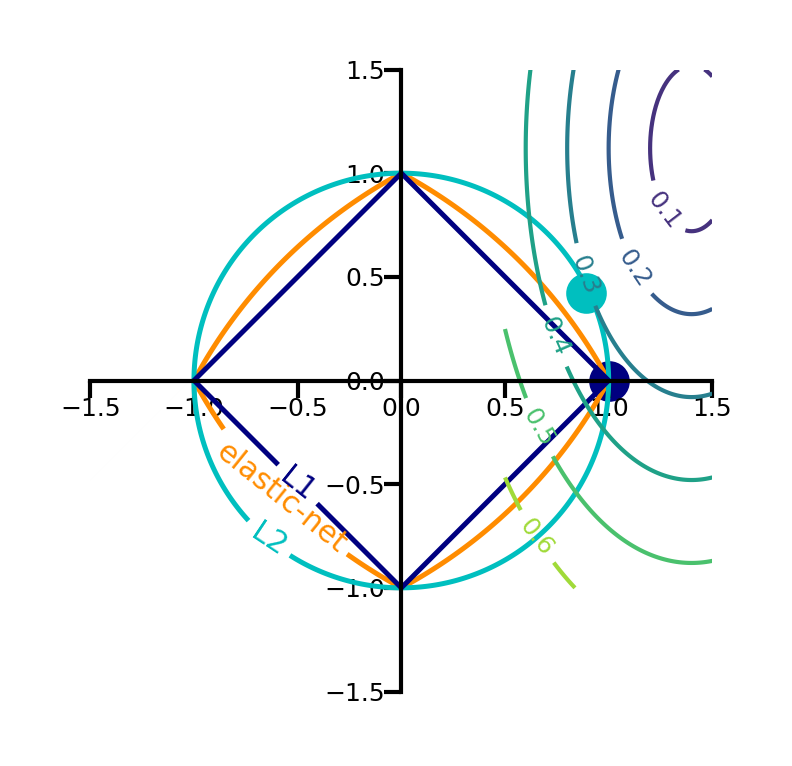
Elastic-Net¶
Adds both L1 and L2 regularization:
is the L1 ratio
With ,
With ,
sets a trade-off between L1 and L2.
Allows learning sparse models (like Lasso) while maintaining L2 regularization benefits
E.g. if 2 features are correlated, Lasso likely picks one randomly, Elastic-Net keeps both
Weights can be optimized using coordinate descent (similar to Lasso)
Other loss functions for regression¶
Huber loss: switches from squared loss to linear loss past a value
More robust against outliers
Epsilon insensitive: ignores errors smaller than , and linear past that
Aims to fit function so that residuals are at most
Also known as Support Vector Regression (
SVRin sklearn)
Squared Epsilon insensitive: ignores errors smaller than , and squared past that
These can all be solved with stochastic gradient descent
SGDRegressorin sklearn
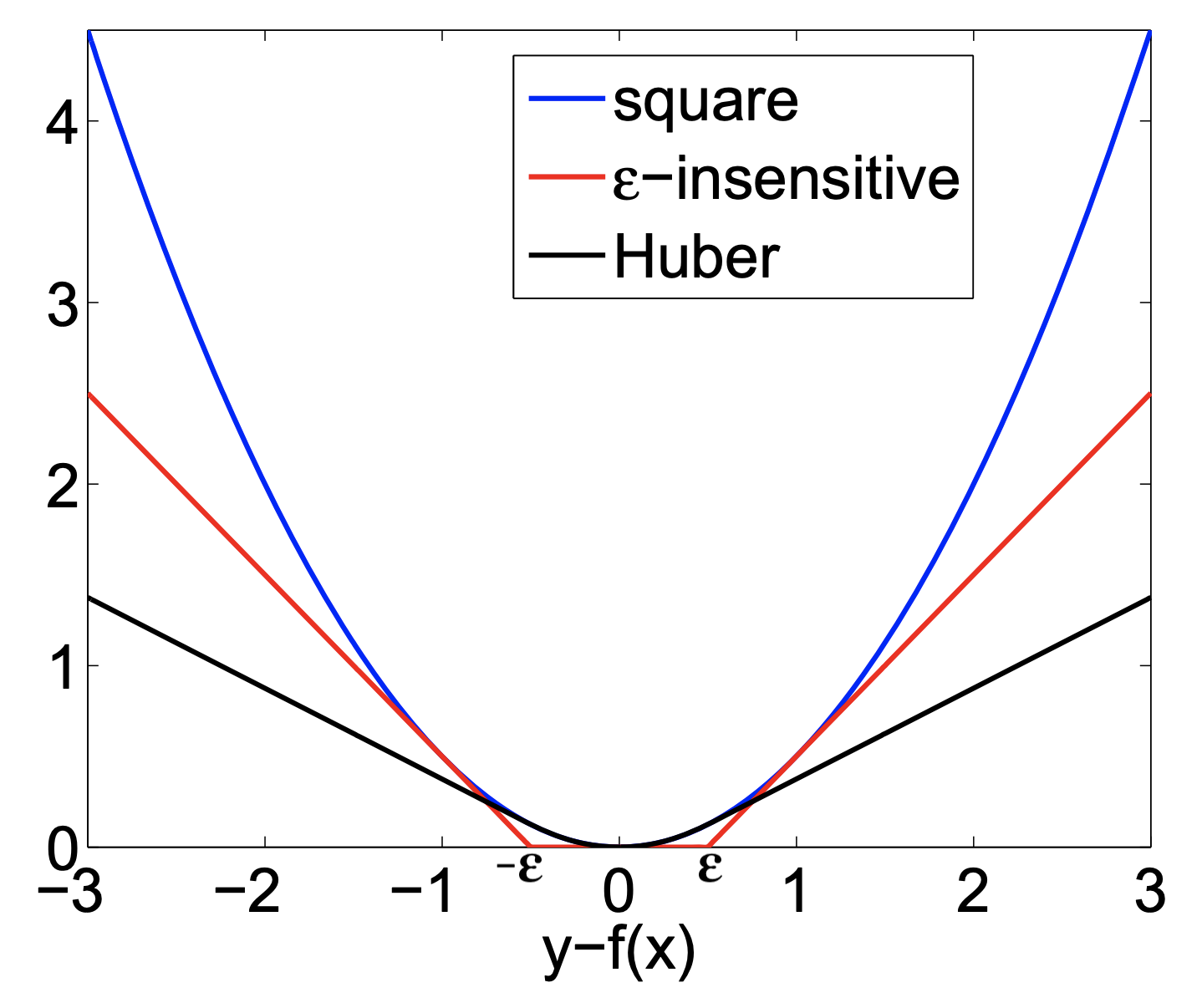
Linear models for Classification¶
Aims to find a hyperplane that separates the examples of each class.
For binary classification (2 classes), we aim to fit the following function:
When , predict class -1, otherwise predict class +1
Source
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
Xf, yf = mglearn.datasets.make_forge()
fig, ax = plt.subplots(figsize=(6*fig_scale,4*fig_scale))
clf = LogisticRegression().fit(Xf, yf)
mglearn.tools.plot_2d_separator(clf, Xf,
ax=ax, alpha=.7, cm=mglearn.cm2)
mglearn.discrete_scatter(Xf[:, 0], Xf[:, 1], yf, ax=ax, s=10*fig_scale)
ax.set_xlabel("Feature 1")
ax.set_ylabel("Feature 2")
ax.legend(['Class -1','Class 1']);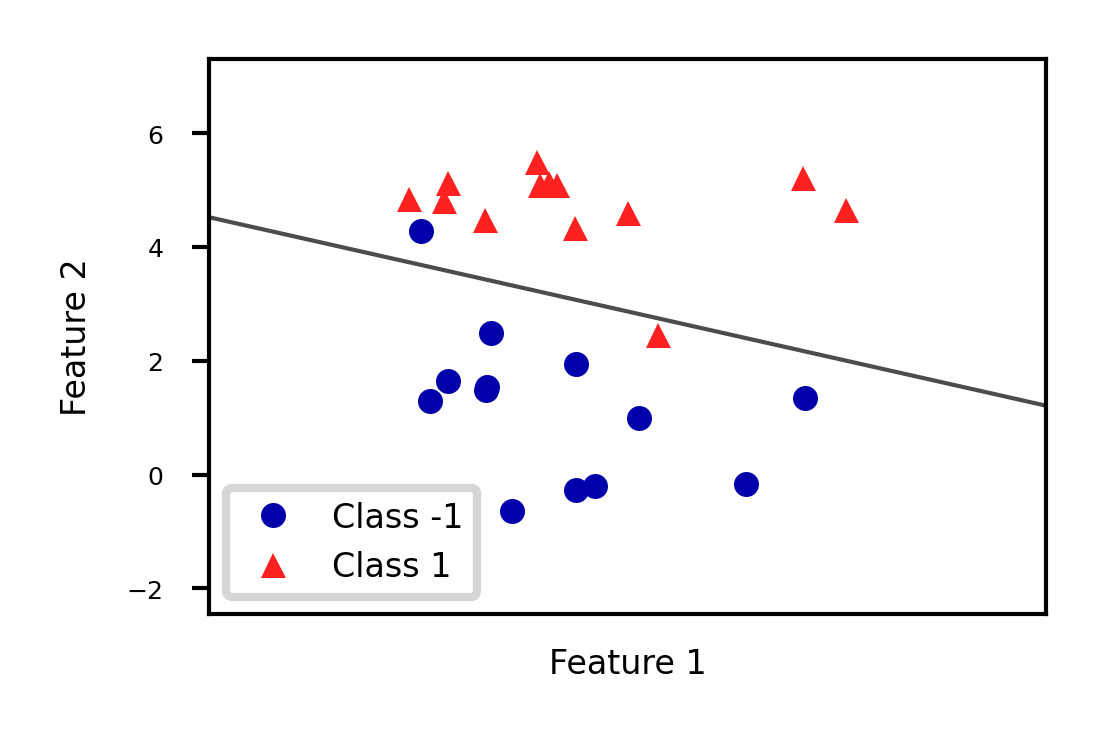
There are many algorithms for linear classification, differing in loss function, regularization techniques, and optimization method
Most common techniques:
Convert target classes {neg,pos} to {0,1} and treat as a regression task
Logistic regression (Log loss)
Ridge Classification (Least Squares + L2 loss)
Find hyperplane that maximizes the margin between classes
Linear Support Vector Machines (Hinge loss)
Neural networks without activation functions
Perceptron (Perceptron loss)
SGDClassifier: can act like any of these by choosing loss function
Hinge, Log, Modified_huber, Squared_hinge, Perceptron
Logistic regression¶
Aims to predict the probability that a point belongs to the positive class
Converts target values {negative (blue), positive (red)} to {0,1}
Fits a logistic (or sigmoid or S curve) function through these points
Maps (-Inf,Inf) to a probability [0,1]
E.g. in 1D:
Source
def sigmoid(x,w1,w0):
return 1 / (1 + np.exp(-(x*w1+w0)))
@interact
def plot_logreg(w0=(-10.0,5.0,1),w1=(-1.0,3.0,0.3)):
fig, ax = plt.subplots(figsize=(8*fig_scale,3*fig_scale))
red = [Xf[i, 1] for i in range(len(yf)) if yf[i]==1]
blue = [Xf[i, 1] for i in range(len(yf)) if yf[i]==0]
ax.scatter(red, [1]*len(red), c='r', label='Positive class')
ax.scatter(blue, [0]*len(blue), c='b', label='Negative class')
x = np.linspace(min(-1, -w0/w1),max(6, -w0/w1))
ax.plot(x,sigmoid(x,w1,w0),lw=2*fig_scale,c='g', label='logistic(x*w1+w0)'.format(np.round(w0,2),np.round(w1,2)))
ax.axvline(x=(-w0/w1), ymin=0, ymax=1, label='Decision boundary')
ax.plot(x,x*w1+w0,lw=2*fig_scale,c='k',linestyle=':', label='y=x*w1+w0')
ax.set_xlabel("Feature")
ax.set_ylabel("y")
ax.set_ylim(-0.05,1.05)
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width * 0.8, box.height]);
plt.show()Source
if not interactive:
# fitted solution
clf2 = LogisticRegression(C=100).fit(Xf[:, 1].reshape(-1, 1), yf)
w0 = clf2.intercept_
w1 = clf2.coef_[0][0]
plot_logreg(w0=w0,w1=w1)Fitted solution to our 2D example:
To get a binary prediction, choose a probability threshold (e.g. 0.5)
Source
lr_clf = LogisticRegression(C=100).fit(Xf, yf)
def sigmoid2d(x1,x2,w0,w1,w2):
return 1 / (1 + np.exp(-(x2*w2+x1*w1+w0)))
@interact
def plot_logistic_fit(rotation=(0,360,10)):
w0 = lr_clf.intercept_
w1 = lr_clf.coef_[0][0]
w2 = lr_clf.coef_[0][1]
# plot surface of f
fig = plt.figure(figsize=(7*fig_scale,5*fig_scale))
ax = plt.axes(projection="3d")
x0 = np.linspace(8, 16, 30)
x1 = np.linspace(-1, 6, 30)
X0, X1 = np.meshgrid(x0, x1)
# Surface
ax.plot_surface(X0, X1, sigmoid2d(X0, X1, w0, w1, w2), rstride=1, cstride=1,
cmap='bwr', edgecolor='none',alpha=0.5,label='sigmoid')
# Points
c=['b','r']
ax.scatter3D(Xf[:, 0], Xf[:, 1], yf, c=[c[i] for i in yf], s=10*fig_scale)
# Decision boundary
# x2 = -(x1*w1 + w0)/w2
ax.plot3D(x0,-(x0*w1 + w0)/w2,[0.5]*len(x0), lw=1*fig_scale, c='k', linestyle=':')
z = np.linspace(0, 1, 31)
XZ, Z = np.meshgrid(x0, z)
YZ = -(XZ*w1 + w0)/w2
ax.plot_wireframe(XZ, YZ, Z, rstride=5, lw=1*fig_scale, cstride=5, alpha=0.3, color='k',label='decision boundary')
ax.tick_params(axis='both', width=0, labelsize=10*fig_scale, pad=-4)
ax.set_xlabel('x0', labelpad=-6)
ax.set_ylabel('x1', labelpad=-6)
ax.get_zaxis().set_ticks([])
ax.view_init(30, rotation) # Use this to rotate the figure
plt.tight_layout()
#plt.legend() # Doesn't work yet, bug in matplotlib
plt.show()Source
if not interactive:
plot_logistic_fit(rotation=150)Loss function: Cross-entropy¶
Models that return class probabilities can use cross-entropy loss
Also known as log loss, logistic loss, or maximum likelihood
Based on true probabilities (0 or 1) and predicted probabilities over instances and classes
Binary case (C=2):
Penalty (a.k.a. ‘surprise’) grows exponentially as difference between and increases
If you are sure of an answer (high ) and it’s wrong (low ), you definitely want to learn
Often used together with L2 (or L1) loss:
Source
def cross_entropy(yHat, y):
if y == 1:
return -np.log(yHat)
else:
return -np.log(1 - yHat)
fig, ax = plt.subplots(figsize=(6*fig_scale,2*fig_scale))
x = np.linspace(0,1,100)
ax.plot(x,cross_entropy(x, 1),lw=2*fig_scale,c='b',label='true label = 1', linestyle='-')
ax.plot(x,cross_entropy(x, 0),lw=2*fig_scale,c='r',label='true label = 0', linestyle='-')
ax.set_xlabel(r"Predicted probability $\hat{y}$")
ax.set_ylabel("Log loss")
plt.grid()
plt.legend();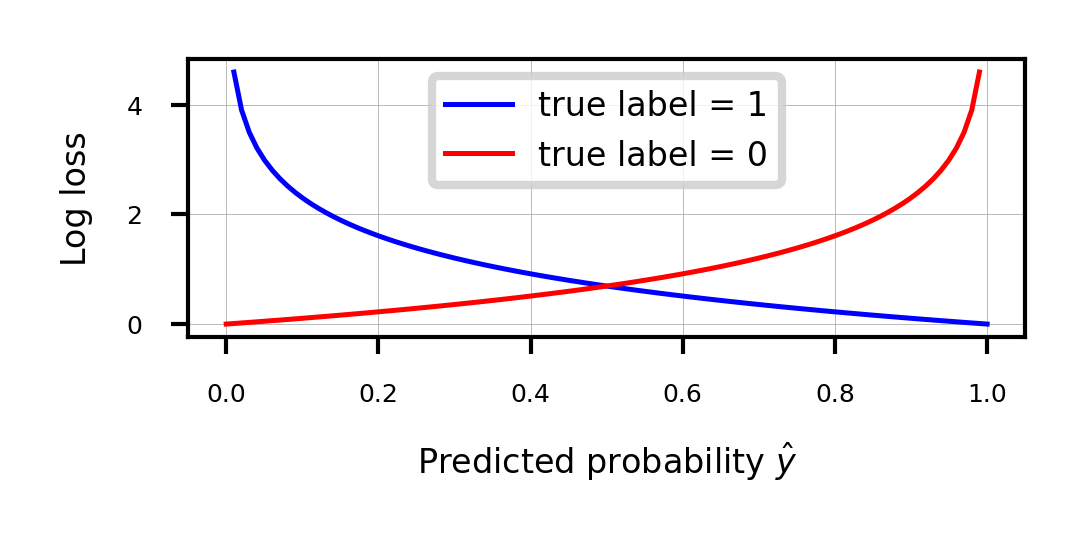
Optimization methods (solvers) for cross-entropy loss¶
Gradient descent (only supports L2 regularization)
Log loss is differentiable, so we can use (stochastic) gradient descent
Variants thereof, e.g. Stochastic Average Gradient (SAG, SAGA)
Coordinate descent (supports both L1 and L2 regularization)
Faster iteration, but may converge more slowly, has issues with saddlepoints
Called
liblinearin sklearn. Can’t run in parallel.
Newton-Rhapson or Newton Conjugate Gradient (only L2):
Uses the Hessian :
Slow for large datasets. Works well if solution space is (near) convex
Quasi-Newton methods (only L2)
Approximate, faster to compute
E.g. Limited-memory Broyden–Fletcher–Goldfarb–Shanno (
lbfgs)Default in sklearn for Logistic Regression
Some hints on choosing solvers
Data scaling helps convergence, minimizes differences between solvers
#### In practice
* Logistic regression can also be found in `sklearn.linear_model`.
* `C` hyperparameter is the _inverse_ regularization strength: $C=\alpha^{-1}$
* `penalty`: type of regularization: L1, L2 (default), Elastic-Net, or None
* `solver`: newton-cg, lbfgs (default), liblinear, sag, saga
* Increasing C: less regularization, tries to overfit individual points
``` python
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C=1).fit(X_train, y_train)
```#### Optimization methods (solvers) for cross-entropy loss
* Gradient descent (only supports L2 regularization)
- Log loss is differentiable, so we can use (stochastic) gradient descent
- Variants thereof, e.g. Stochastic Average Gradient (SAG, SAGA)
* Coordinate descent (supports both L1 and L2 regularization)
- Faster iteration, but may converge more slowly, has issues with saddlepoints
- Called `liblinear` in sklearn. Can't run in parallel.
* Newton-Rhapson or Newton Conjugate Gradient (only L2):
- Uses the Hessian $H = \big[\frac{\partial^2 \mathcal{L}}{\partial x_i \partial x_j} \big]$: $\mathbf{w}^{s+1} = \mathbf{w}^s-\eta H^{-1}(\mathbf{w}^s) \nabla \mathcal{L}(\mathbf{w}^s)$
- Slow for large datasets. Works well if solution space is (near) convex
* Quasi-Newton methods (only L2)
- Approximate, faster to compute
- E.g. Limited-memory Broyden–Fletcher–Goldfarb–Shanno (`lbfgs`)
- Default in sklearn for Logistic Regression
* [Some hints on choosing solvers](https://dev.to/discdiver/don-t-sweat-the-solver-stuff-20np)
- Data scaling helps convergence, minimizes differences between solversSource
from sklearn.linear_model import LogisticRegression
@interact
def plot_lr(C_log=(-3,4,0.1)):
# Still using artificial data
fig, ax = plt.subplots(figsize=(6*fig_scale,3*fig_scale))
mglearn.discrete_scatter(Xf[:, 0], Xf[:, 1], yf, ax=ax, s=10*fig_scale)
lr = LogisticRegression(C=10**C_log).fit(Xf, yf)
w = lr.coef_[0]
xx = np.linspace(7, 13)
yy = (-w[0] * xx - lr.intercept_[0]) / w[1]
ax.plot(xx, yy, c='k')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title("C = {:.3f}, w1={:.3f}, w2={:.3f}".format(10**C_log,w[0],w[1]))
ax.legend(loc="best");
plt.show()Source
if not interactive:
plot_lr(C_log=(4))Analyze behavior on the breast cancer dataset
Underfitting if C is too small, some overfitting if C is too large
We use cross-validation because the dataset is small
Source
from sklearn.datasets import fetch_openml
from sklearn.model_selection import cross_validate
spam_data = fetch_openml(name="qsar-biodeg", as_frame=True)
X_C, y_C = spam_data.data, spam_data.target
C=np.logspace(-3,6,num=19)
test_score=[]
train_score=[]
for c in C:
lr = LogisticRegression(C=c)
scores = cross_validate(lr,X_C,y_C,cv=10, return_train_score=True)
test_score.append(np.mean(scores['test_score']))
train_score.append(np.mean(scores['train_score']))
fig, ax = plt.subplots(figsize=(6*fig_scale,4*fig_scale))
ax.set_xticks(range(19))
ax.set_xticklabels(np.round(C,3))
ax.set_xlabel('C')
ax.plot(test_score, lw=2*fig_scale, label='test score')
ax.plot(train_score, lw=2*fig_scale, label='train score')
ax.legend()
plt.xticks(rotation=45);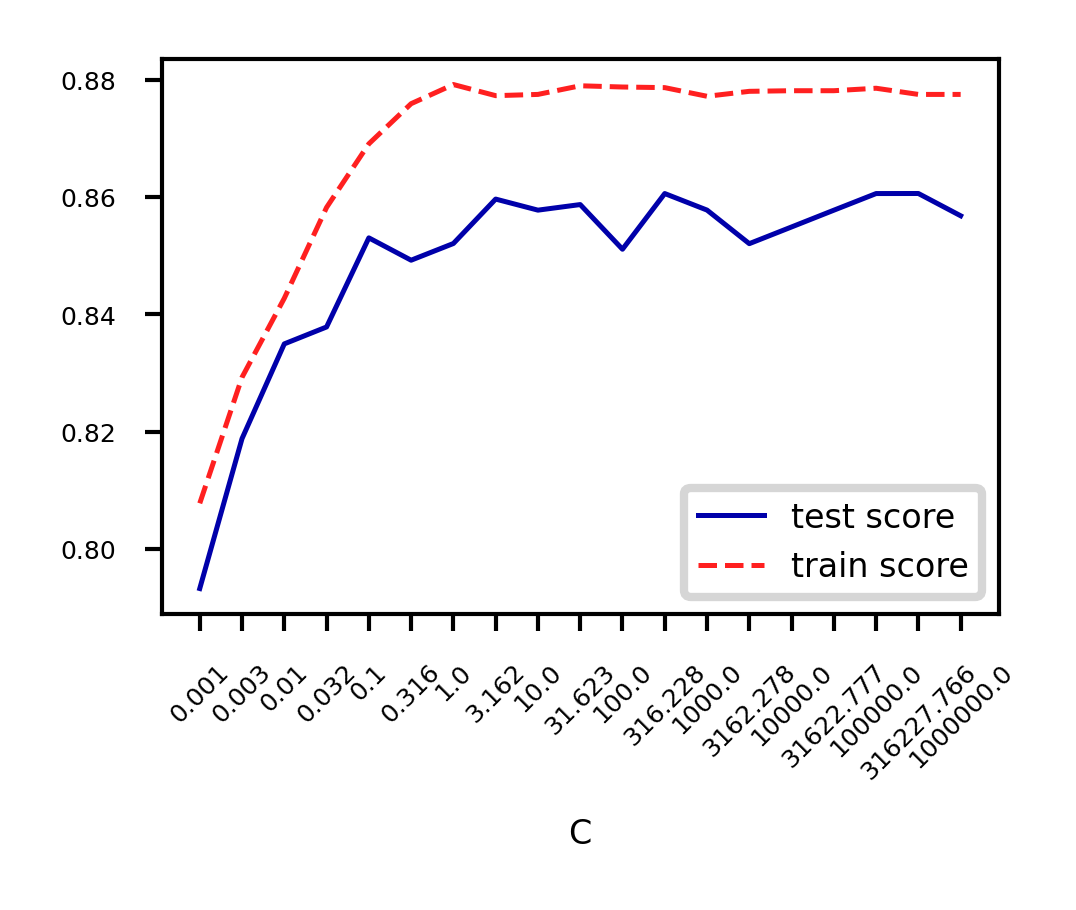
Again, choose between L1 or L2 regularization (or elastic-net)
Small C overfits, L1 leads to sparse models
Source
X_C_train, X_C_test, y_C_train, y_C_test = train_test_split(X_C, y_C, random_state=0)
@interact
def plot_logreg(C=(0.01,1000.0,0.1), penalty=['l1','l2']):
r = LogisticRegression(C=C, penalty=penalty, solver='liblinear').fit(X_C_train, y_C_train)
fig, ax = plt.subplots(figsize=(8*fig_scale,1.9*fig_scale))
ax.plot(r.coef_.T, 'o', markersize=6*fig_scale)
ax.set_title("C: {:.3f}, penalty: {}, score {:.2f} (training score {:.2f})".format(C, penalty, r.score(X_C_test, y_C_test), r.score(X_C_train, y_C_train)),pad=0)
ax.set_xlabel("Coefficient index", labelpad=0)
ax.set_ylabel("Coeff. magnitude", labelpad=0, fontsize=10*fig_scale)
ax.tick_params(axis='both', pad=0)
ax.hlines(0, 40, len(r.coef_)-1)
ax.set_ylim(-10, 10)
ax.set_xlim(0, 40);
plt.tight_layout();
plt.show();Source
if not interactive:
plot_logreg(0.001, 'l2')
plot_logreg(100, 'l2')
plot_logreg(100, 'l1')Ridge Classification¶
Instead of log loss, we can also use ridge loss:
In this case, target values {negative, positive} are converted to {-1,1}
Can be solved similarly to Ridge regression:
Closed form solution (a.k.a. Cholesky)
Gradient descent and variants
E.g. Conjugate Gradient (CG) or Stochastic Average Gradient (SAG,SAGA)
Use Cholesky for smaller datasets, Gradient descent for larger ones
Support vector machines¶
Decision boundaries close to training points may generalize badly
Very similar (nearby) test point are classified as the other class
Choose a boundary that is as far away from training points as possible
The support vectors are the training samples closest to the hyperplane
The margin is the distance between the separating hyperplane and the support vectors
Hence, our objective is to maximize the margin
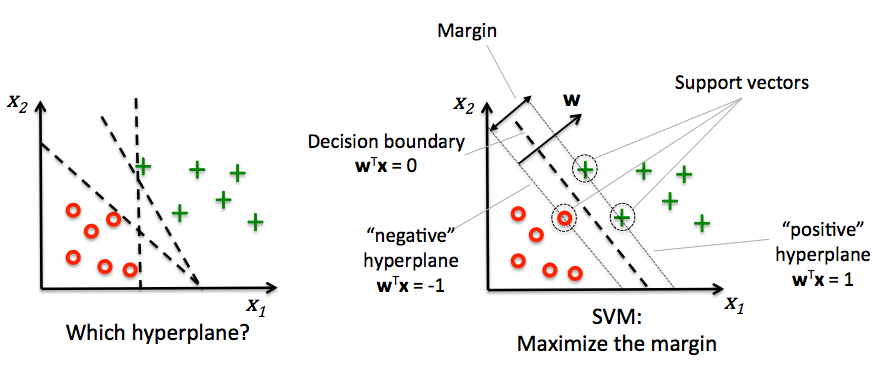
Solving SVMs with Lagrange Multipliers¶
Imagine a hyperplane (green) that has slope , value ‘+1’ for the positive (red) support vectors, and ‘-1’ for the negative (blue) ones
Margin between the boundary and support vectors is , with
We want to find the weights that maximize . We can also do that by maximizing
Source
from sklearn.svm import SVC
# we create 40 separable points
np.random.seed(0)
sX = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
sY = [0] * 20 + [1] * 20
# fit the model
s_clf = SVC(kernel='linear')
s_clf.fit(sX, sY)
@interact
def plot_svc_fit(rotationX=(0,20,1),rotationY=(90,180,1)):
# get the separating hyperplane
w = s_clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-5, 5)
yy = a * xx - (s_clf.intercept_[0]) / w[1]
zz = np.linspace(-2, 2, 30)
# plot the parallels to the separating hyperplane that pass through the
# support vectors
b = s_clf.support_vectors_[0]
yy_down = a * xx + (b[1] - a * b[0])
b = s_clf.support_vectors_[-1]
yy_up = a * xx + (b[1] - a * b[0])
# plot the line, the points, and the nearest vectors to the plane
fig = plt.figure(figsize=(7*fig_scale,4.5*fig_scale))
ax = plt.axes(projection="3d")
ax.plot3D(xx, yy, [0]*len(xx), 'k-')
ax.plot3D(xx, yy_down, [0]*len(xx), 'k--')
ax.plot3D(xx, yy_up, [0]*len(xx), 'k--')
ax.scatter3D(s_clf.support_vectors_[:, 0], s_clf.support_vectors_[:, 1], [0]*len(s_clf.support_vectors_[:, 0]),
s=85*fig_scale, edgecolors='k', c='w')
ax.scatter3D(sX[:, 0], sX[:, 1], [0]*len(sX[:, 0]), c=sY, cmap=plt.cm.bwr, s=10*fig_scale )
# Planes
XX, YY = np.meshgrid(xx, yy)
if interactive:
ZZ = w[0]*XX+w[1]*YY+clf.intercept_[0]
else: # rescaling (for prints) messes up the Z values
ZZ = w[0]*XX/fig_scale+w[1]*YY/fig_scale+clf.intercept_[0]*fig_scale/2
ax.plot_wireframe(XX, YY, XX*0, rstride=5, cstride=5, alpha=0.3, color='k', label='XY plane')
ax.plot_wireframe(XX, YY, ZZ, rstride=5, cstride=5, alpha=0.3, color='g', label='hyperplane')
ax.set_axis_off()
ax.view_init(rotationX, rotationY) # Use this to rotate the figure
ax.dist = 6
plt.tight_layout()
plt.show()Source
if not interactive:
plot_svc_fit(9,135)Geometric interpretation¶
We want to maximize (blue contours)
The hyperplane (red) must be for all positive examples:
Find the weights that satify but maximize
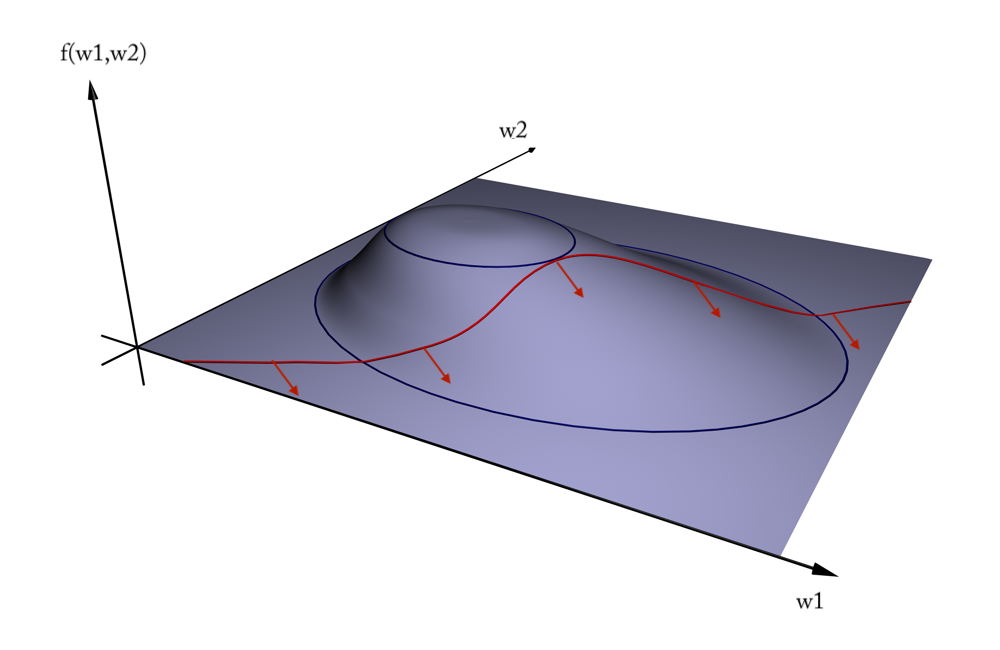
Solution¶
A quadratic loss function with linear constraints can be solved with Lagrangian multipliers
This works by assigning a weight (called a dual coefficient) to every data point
They reflect how much individual points influence the weights
The points with non-zero are the support vectors
Next, solve the following Primal objective:
is the correct class for example
so that
It has a Dual formulation as well (See ‘Elements of Statistical Learning’ for the full derivation):
so that
Computes the dual coefficients directly. A number of these are non-zero (sparseness).
Dot product can be interpreted as the closeness between points and
We can replace the dot product with other similarity functions (kernels)
increases if nearby support vectors with high weights have different class
also increases with the number of support vectors and their weights
Can be solved with quadratic programming, e.g. Sequential Minimal Optimization (SMO)
Example result. The circled samples are support vectors, together with their coefficients.
Source
from sklearn.svm import SVC
# Plot SVM support vectors
def plot_linear_svm(X,y,C,ax):
clf = SVC(kernel='linear', C=C)
clf.fit(X, y)
# get the separating hyperplane
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-5, 5)
yy = a * xx - (clf.intercept_[0]) / w[1]
# plot the parallels to the separating hyperplane
yy_down = (-1-w[0]*xx-clf.intercept_[0])/w[1]
yy_up = (1-w[0]*xx-clf.intercept_[0])/w[1]
# plot the line, the points, and the nearest vectors to the plane
ax.set_title('C = %s' % C)
ax.plot(xx, yy, 'k-')
ax.plot(xx, yy_down, 'k--')
ax.plot(xx, yy_up, 'k--')
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
s=85*fig_scale, edgecolors='gray', c='w', zorder=10, lw=1*fig_scale)
ax.scatter(X[:, 0], X[:, 1], c=y, zorder=10, cmap=plt.cm.bwr)
ax.axis('tight')
# Add coefficients
for i, coef in enumerate(clf.dual_coef_[0]):
ax.annotate("%0.2f" % (coef), (clf.support_vectors_[i, 0]+0.1,clf.support_vectors_[i, 1]+0.35), fontsize=10*fig_scale, zorder=11)
ax.set_xlim(np.min(X[:, 0])-0.5, np.max(X[:, 0])+0.5)
ax.set_ylim(np.min(X[:, 1])-0.5, np.max(X[:, 1])+0.5)
ax.set_xticks(())
ax.set_yticks(())
# we create 40 separable points
np.random.seed(0)
svm_X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
svm_Y = [0] * 20 + [1] * 20
svm_fig, svm_ax = plt.subplots(figsize=(8*fig_scale,5*fig_scale))
plot_linear_svm(svm_X,svm_Y,1,svm_ax)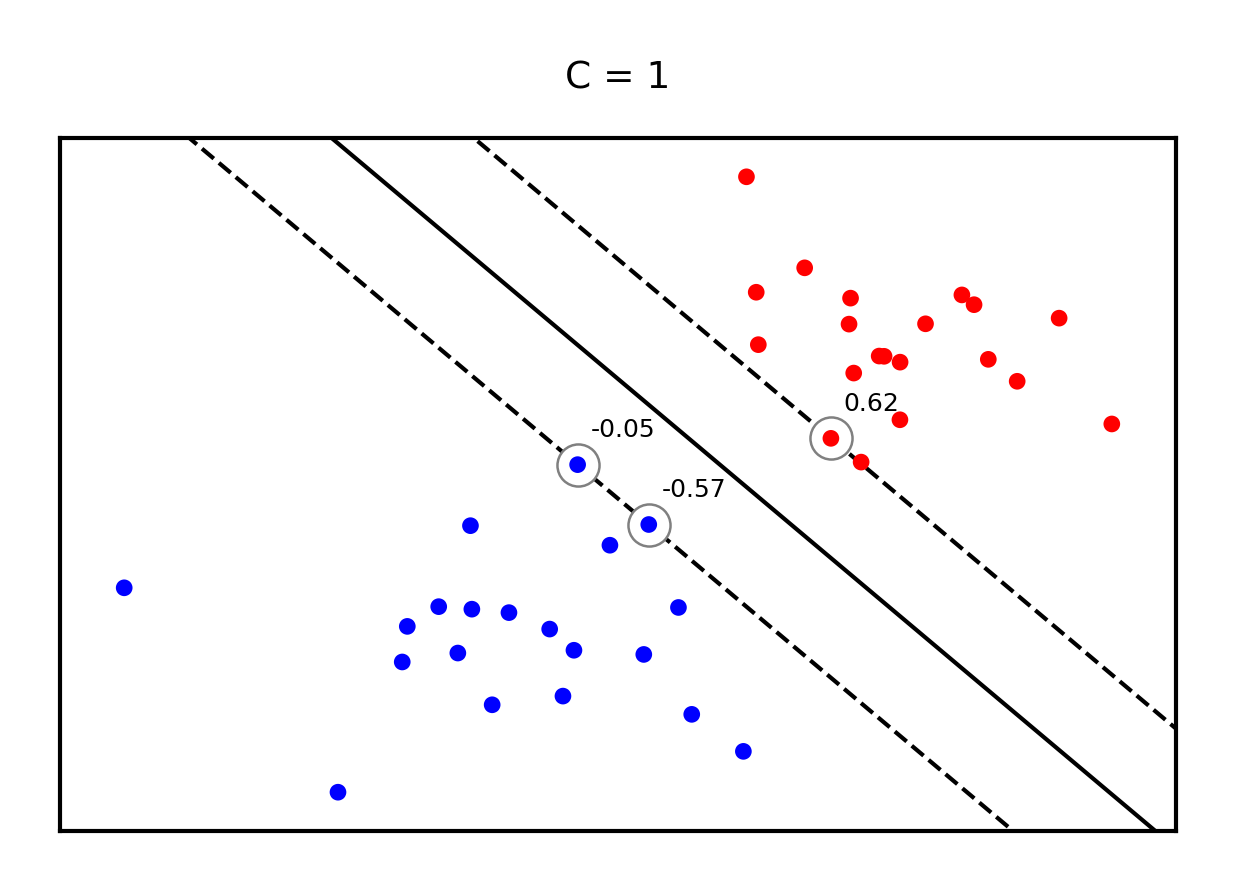
Making predictions¶
will be 0 if the training point lies on the right side of the decision boundary and outside the margin
The training samples for which is not 0 are the support vectors
Hence, the SVM model is completely defined by the support vectors and their dual coefficients (weights)
Knowing the dual coefficients , we can find the weights for the maximal margin separating hyperplane
And we could classify a new sample by looking at the sign of
However, we don’t need to compute to make predictions. We only need to look at the support vectors.
SVMs and kNN¶
Remember, we will classify a new point by looking at the sign of:
Weighted k-nearest neighbor is a generalization of the k-nearest neighbor classifier. It classifies points by evaluating:
Hence: SVM’s predict much the same way as k-NN, only:
They only consider the truly important points (the support vectors): much faster
The number of neighbors is the number of support vectors
The distance function is an inner product of the inputs (or another kernel)
Given , we predict by looking at the classes of the support vectors, weighted by their distance.
Regularized (soft margin) SVMs¶
If the data is not linearly separable, (hard) margin maximization becomes meaningless
Relax the contraint by allowing an error :
Or (since ):
The sum over all points is called hinge loss:
Attenuating the error component with a hyperparameter , we get the objective
Can still be solved with quadratic programming
Source
def hinge_loss(yHat, y):
if y == 1:
return np.maximum(0,1-yHat)
else:
return np.maximum(0,1+yHat)
fig, ax = plt.subplots(figsize=(6*fig_scale,2*fig_scale))
x = np.linspace(-2,2,100)
ax.plot(x,hinge_loss(x, 1),lw=2*fig_scale,c='b',label='true label = 1', linestyle='-')
ax.plot(x,hinge_loss(x, 0),lw=2*fig_scale,c='r',label='true label = 0', linestyle='-')
ax.set_xlabel(r"Prediction value $\hat{y}$")
ax.set_ylabel("Hinge loss")
plt.grid()
plt.legend();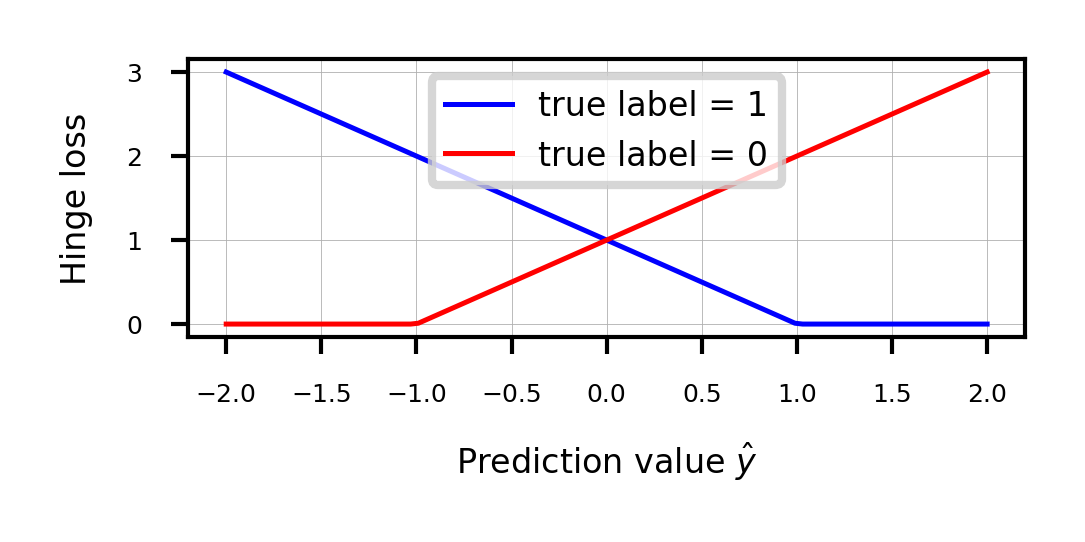
Sidenote: Least Squares SVMs¶
We can also use the squares of all the errors, or squared hinge loss:
This yields the Least Squares SVM objective
Can be solved with Lagrangian Multipliers and a set of linear equations
Still yields support vectors and still allows kernelization
Support vectors are not sparse, but pruning techniques exist
Source
fig, ax = plt.subplots(figsize=(6*fig_scale,2*fig_scale))
x = np.linspace(-2,2,100)
ax.plot(x,hinge_loss(x, 1)** 2,lw=2*fig_scale,c='b',label='true label = 1', linestyle='-')
ax.plot(x,hinge_loss(x, 0)** 2,lw=2*fig_scale,c='r',label='true label = 0', linestyle='-')
ax.set_xlabel(r"Prediction value $\hat{y}$")
ax.set_ylabel("Squared hinge loss")
plt.grid()
plt.legend();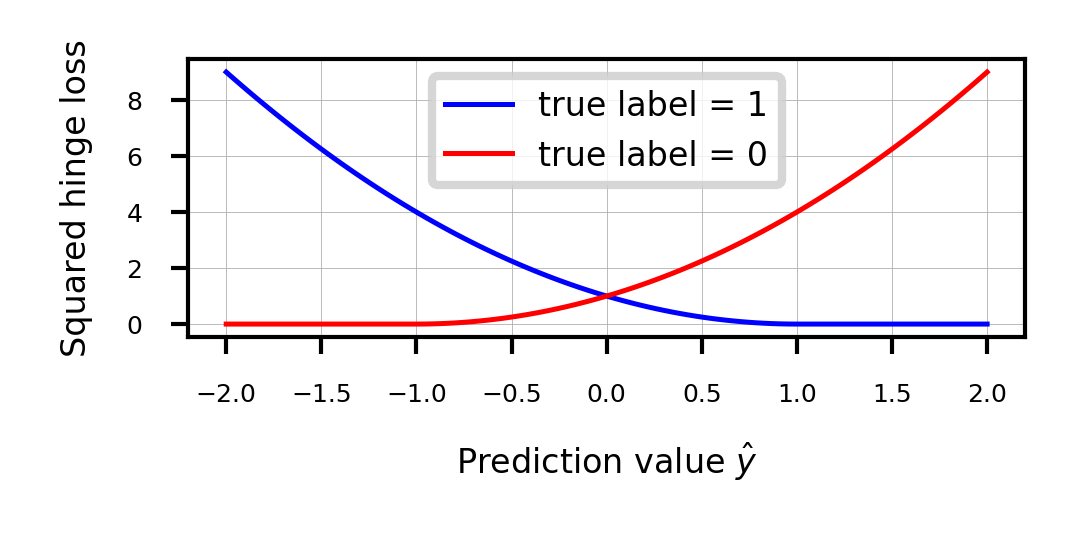
Effect of regularization on margin and support vectors¶
SVM’s Hinge loss acts like L1 regularization, yields sparse models
C is the inverse regularization strength (inverse of in Lasso)
Larger C: fewer support vectors, smaller margin, more overfitting
Smaller C: more support vectors, wider margin, less overfitting
Needs to be tuned carefully to the data
Source
fig, svm_axes = plt.subplots(nrows=1, ncols=2, figsize=(12*fig_scale, 4*fig_scale))
plot_linear_svm(svm_X,svm_Y,1,svm_axes[0])
plot_linear_svm(svm_X,svm_Y,0.05,svm_axes[1])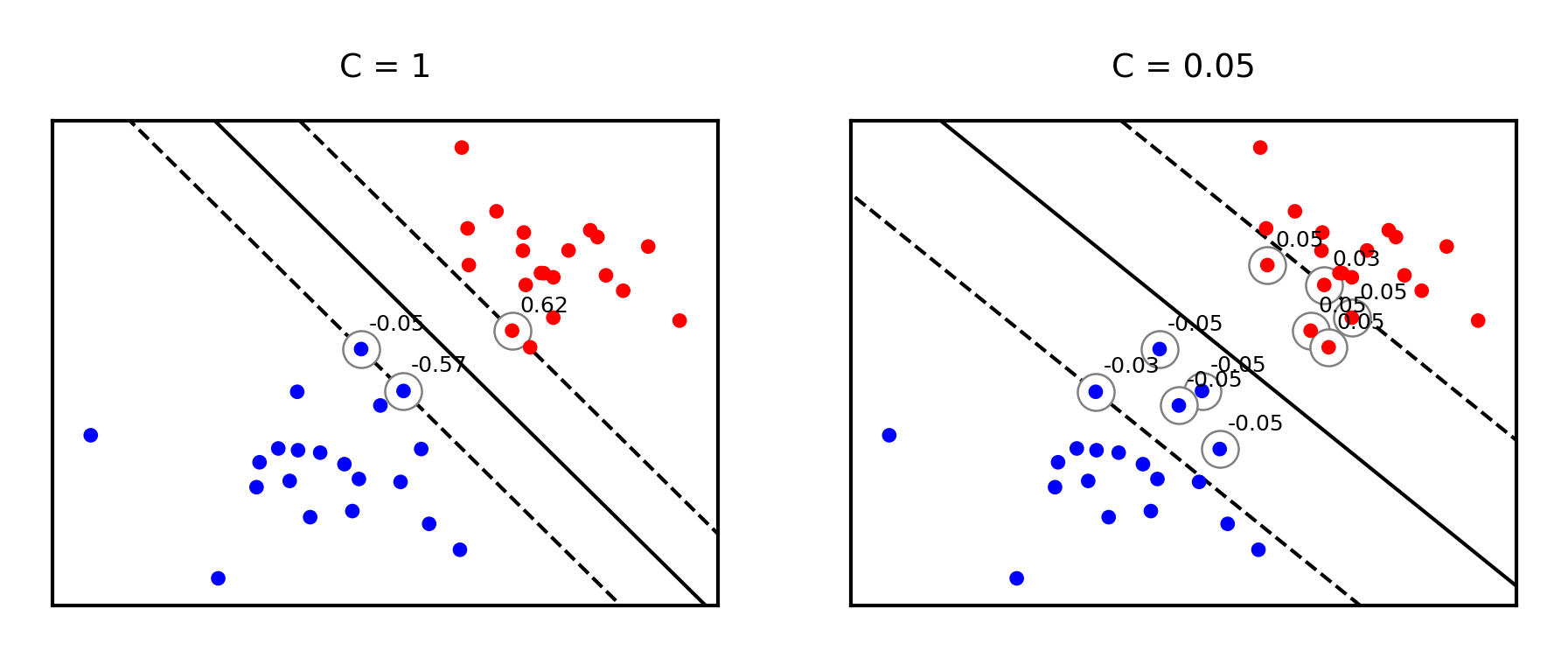
Same for non-linearly separable data
Source
svm_X = np.r_[np.random.randn(20, 2) - [1, 1], np.random.randn(20, 2) + [1, 1]]
fig, svm_axes = plt.subplots(nrows=1, ncols=2, figsize=(12*fig_scale, 5*fig_scale))
plot_linear_svm(svm_X,svm_Y,1,svm_axes[0])
plot_linear_svm(svm_X,svm_Y,0.05,svm_axes[1])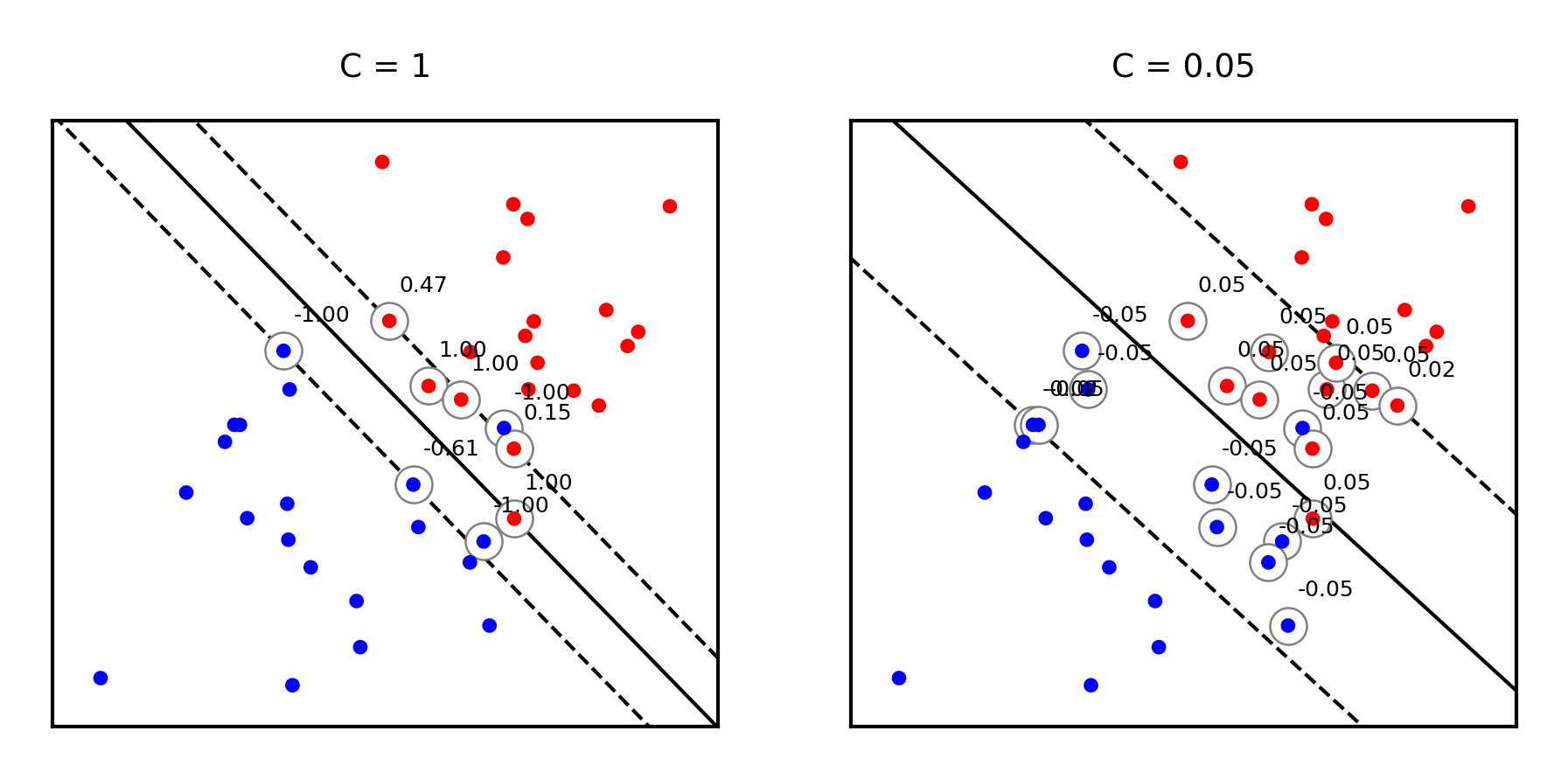
Large C values can lead to overfitting (e.g. fitting noise), small values can lead to underfitting
Source
mglearn.plots.plot_linear_svc_regularization()
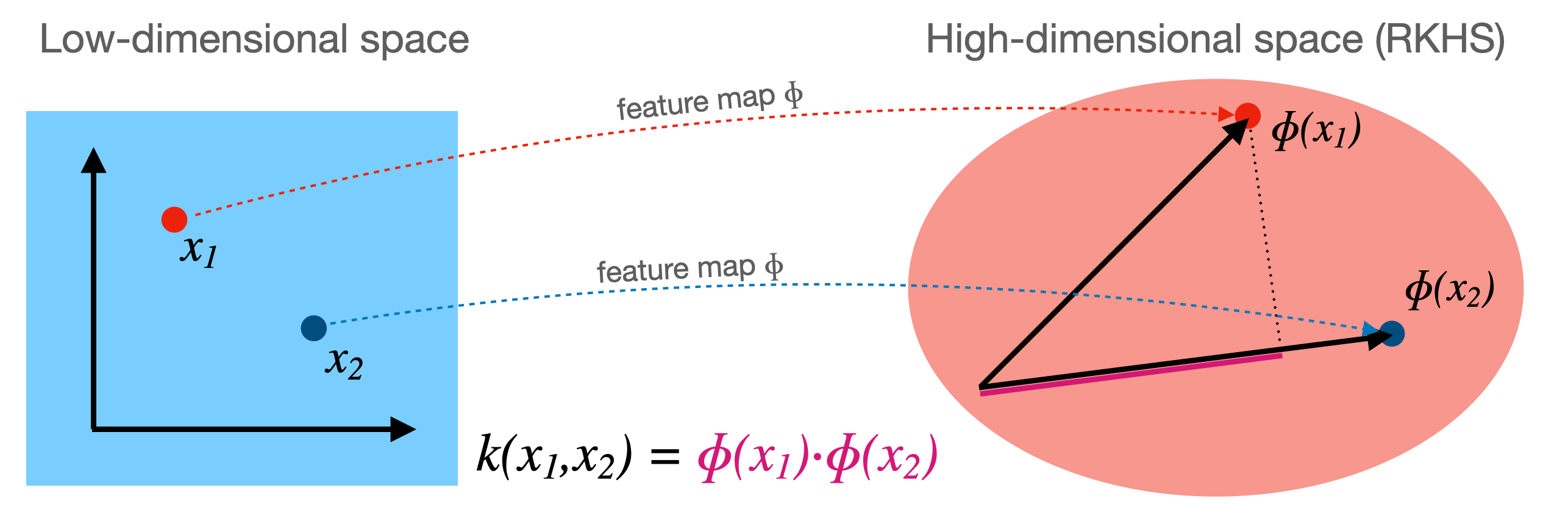
Kernelization¶
Sometimes we can separate the data better by first transforming it to a higher dimensional space
This transformation is called a feature map (but can be expensive)
For certain , we know the function that computes the dot product in :
This kernel function computes the dot product without having to construct (reproduce)
Kernel trick: if your loss function has a dot product, you can simply replace it with a kernel!
For SVMs (in dual form), replacing yields a kernelized SVM:
Polynomial kernel¶
The polynomial kernel (for degree ) reproduces the polynomial feature map
It can be easily computed from the original dot product:
It has two more hyperparameters, but you can usually leave them at default
is a scaling hyperparameter (default )
is a hyperparameter (default 1) to trade off influence of higher-order terms
By simply replacing the dot product with a kernel we can learn non-linear SVMs!
It is technically still linear in , but in our original space the boundary becomes a polynomial curve
Prediction still happens as before, but the influence of each support vector drops of polynomially (with degree )
from sklearn import svm
def plot_svm_kernels(kernels, poly_degree=3, gamma=2, C=1, size=4):
# Our dataset and targets
X = np.c_[(.4, -.7),
(-1.5, -1),
(-1.4, -.9),
(-1.3, -1.2),
(-1.1, -.2),
(-1.2, -.4),
(-.5, 1.2),
(-1.5, 2.1),
(1, 1),
# --
(1.3, .8),
(1.2, .5),
(.2, -2),
(.5, -2.4),
(.2, -2.3),
(0, -2.7),
(1.3, 2.1)].T
Y = [0] * 8 + [1] * 8
# figure number
fig, axes = plt.subplots(-(-len(kernels)//3), min(len(kernels),3), figsize=(min(len(kernels),3)*size*1.2*fig_scale, -(-len(kernels)//3)*size*fig_scale), tight_layout=True)
if len(kernels) == 1:
axes = np.array([axes])
if not isinstance(gamma,list):
gamma = [gamma]*len(kernels)
if not isinstance(C,list):
C = [C]*len(kernels)
# fit the model
for kernel, ax, g, c in zip(kernels,axes.reshape(-1),gamma,C):
clf = svm.SVC(kernel=kernel, gamma=g, C=c, degree=poly_degree)
clf.fit(X, Y)
# plot the line, the points, and the nearest vectors to the plane
if kernel == 'rbf':
ax.set_title(r"kernel = {}, $\gamma$={}, C={}".format(kernel, g, c), pad=0.1)
else:
ax.set_title('kernel = %s' % kernel,pad=0.1)
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
s=25, edgecolors='grey', c='w', zorder=10, linewidths=0.5)
ax.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.bwr, s=10*fig_scale)
for i, coef in enumerate(clf.dual_coef_[0]):
ax.annotate("%0.2f" % (coef), (clf.support_vectors_[i, 0]+0.1,clf.support_vectors_[i, 1]+0.25), zorder=11, fontsize=3)
ax.axis('tight')
x_min = -3
x_max = 3
y_min = -3
y_max = 3
XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()])
# Put the result into a color plot
Z = Z.reshape(XX.shape)
#plt.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.bwr, alpha=0.1)
ax.contour(XX, YY, Z, colors=['k', 'k', 'k', 'k', 'k'], linestyles=['--', ':', '-', ':', '--'],
levels=[-1, -0.5, 0, 0.5, 1])
ax.set_xlim(x_min, x_max)
ax.set_ylim(y_min, y_max)
ax.set_xticks([])
ax.set_yticks([])
plt.tight_layout()
plt.show()
plot_svm_kernels(['linear', 'poly'],poly_degree=3,size=3.5)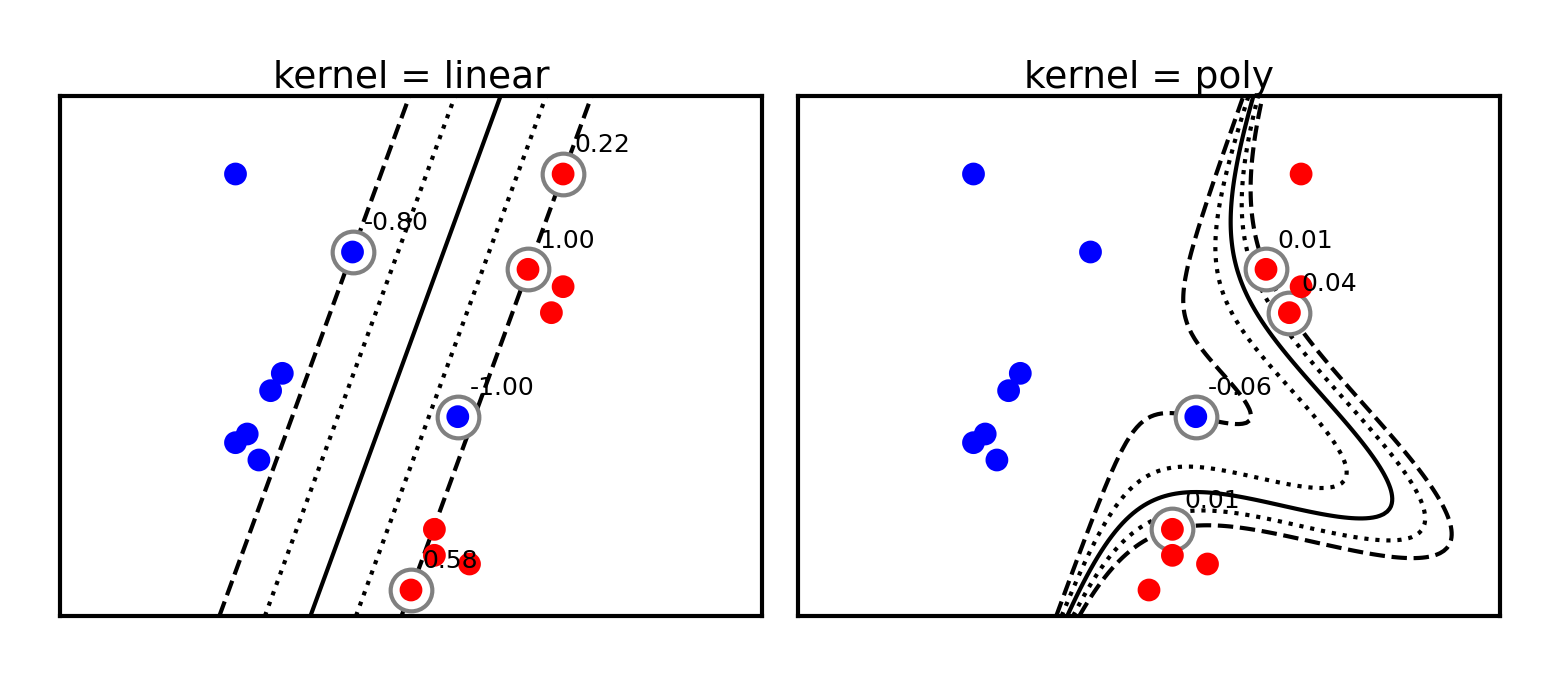
Radial Basis Function (RBF) kernel¶
The RBF or Gaussian kernel (of width ) is related to the Taylor series expansion of
It is a function of how closely together two data points are:
The influence of a point on point drops off exponentially with its distance to
The influence of each support vector now drops of exponentially
Hence, predictions are only affected by very nearby support vectors
RBF kernels are therefore called local kernels
plot_svm_kernels(['linear', 'rbf'],poly_degree=3,gamma=2,size=4)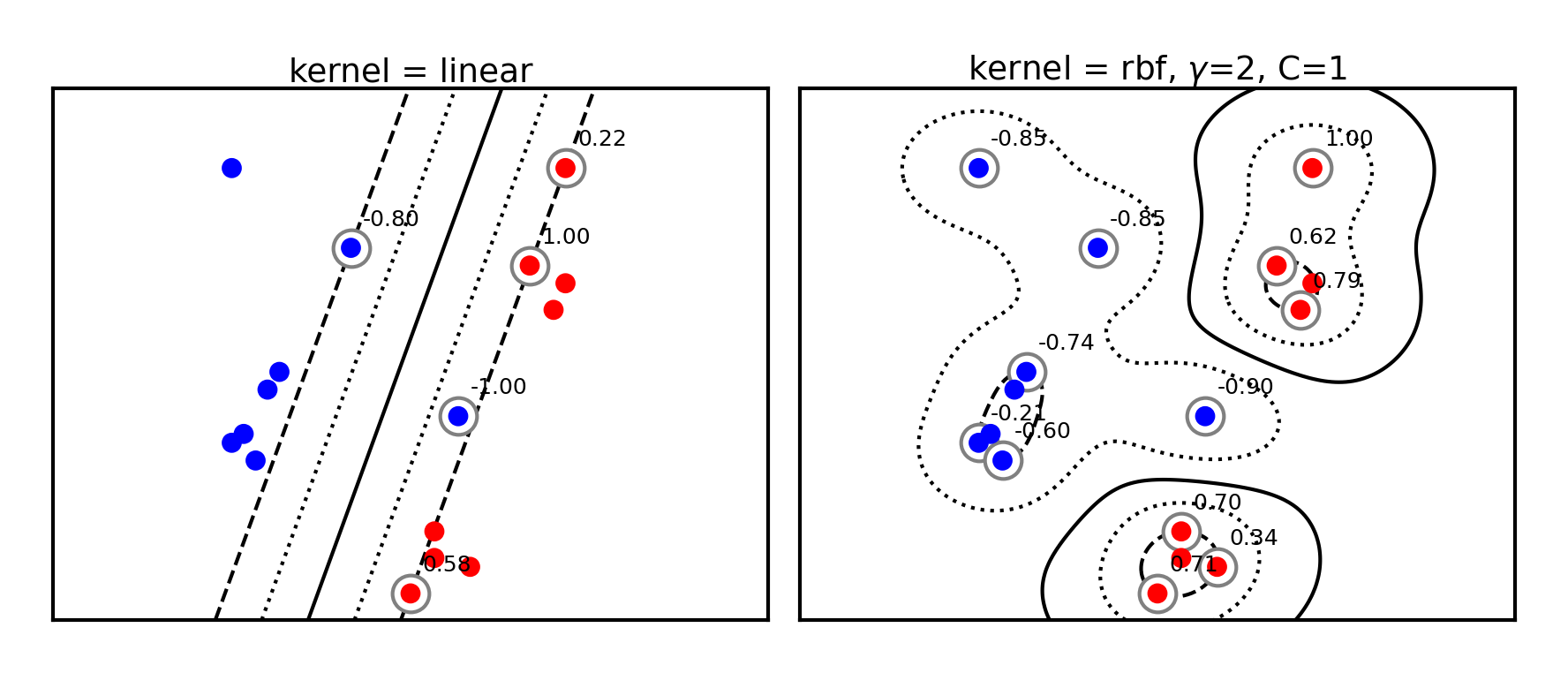
The kernel width () defines how sharply the local influence decays
Acts as a regularizer: low causes underfitting and high causes overfitting
SVM’s C parameter (inverse regularizer) is still at play and thus interacts with
@interact
def plot_rbf_data(gamma=(0.1,10,0.5),C=(0.01,5,0.1)):
plot_svm_kernels(['rbf'],gamma=gamma,C=C,size=5)if not interactive:
plot_svm_kernels(['rbf'],gamma=0.5,C=1,size=5)Kernelization sidenotes (optional)¶
You can invent many more feature maps and corresponding kernels (eg. for text, graphs,...)
However, learning deep learning embeddings from lots of data often works better
You can also kernelize Ridge regression, Logistic regression, Perceptrons, Support Vector Regression,...
The Representer theorem will give you the corresponding loss function
For more detail see the Kernelization lecture under extra materials.
SVMs in scikit-learn¶
svm.LinearSVC: faster for large datasetsAllows choosing between the primal or dual. Primal recommended when >>
Returns
coef_() andintercept_()
svm.SVCallows different kernels to be usedAlso returns
support_vectors_(the support vectors) and thedual_coef_Scales at least quadratically with the number of samples
svm.LinearSVRandsvm.SVRare variants for regression
clf = svm.SVC(kernel='linear') # or 'RBF' or 'Poly'
clf.fit(X, Y)
print("Support vectors:", clf.support_vectors_[:])
print("Coefficients:", clf.dual_coef_[:])Source
from sklearn import svm
# Linearly separable dat
np.random.seed(0)
X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
Y = [0] * 20 + [1] * 20
# Fit the model
clf = svm.SVC(kernel='linear')
clf.fit(X, Y)
# Get the support vectors and weights
print("Support vectors:")
print(clf.support_vectors_[:])
print("Coefficients:")
print(clf.dual_coef_[:])Support vectors:
[[-1.021 0.241]
[-0.467 -0.531]
[ 0.951 0.58 ]]
Coefficients:
[[-0.048 -0.569 0.617]]
Solving SVMs with Gradient Descent¶
SVMs can, alternatively, be solved using gradient decent
Good for large datasets, but does not yield support vectors or kernelization
Hinge loss is not differentiable but convex, and has a subgradient:
Can be solved with (stochastic) gradient descent
Generalized SVMs¶
There are many smoothed versions of hinge loss:
Squared hinge loss:
Also known as Ridge classification
Least Squares SVM: allows kernelization (using a linear equation solver)
Modified Huber loss: squared hinge, but linear after -1. Robust against outliers
Log loss: equivalent to logistic regression
In sklearn,
SGDClassifiercan be used with any of these. Good for large datasets.
Source
def modified_huber_loss(y_true, y_pred):
z = y_pred * y_true
loss = -4 * z
loss[z >= -1] = (1 - z[z >= -1]) ** 2
loss[z >= 1.] = 0
return loss
xmin, xmax = -4, 4
xx = np.linspace(xmin, xmax, 100)
lw = 2*fig_scale
fig, ax = plt.subplots(figsize=(8*fig_scale,4*fig_scale))
plt.plot([xmin, 0, 0, xmax], [1, 1, 0, 0], 'k-', lw=lw,
label="Zero-one loss")
plt.plot(xx, np.where(xx < 1, 1 - xx, 0), 'b-', lw=lw,
label="Hinge loss")
plt.plot(xx, -np.minimum(xx, 0), color='yellowgreen', lw=lw,
label="Perceptron loss")
plt.plot(xx, np.log2(1 + np.exp(-xx)), 'r-', lw=lw,
label="Log loss")
plt.plot(xx, np.where(xx < 1, 1 - xx, 0) ** 2, 'c-', lw=lw,
label="Squared hinge loss")
plt.plot(xx, modified_huber_loss(xx, 1), color='darkorchid', lw=lw,
linestyle='--', label="Modified Huber loss")
plt.ylim((0, 7))
plt.legend(loc="upper right")
plt.xlabel(r"Decision function $f(x)$")
plt.ylabel("$Loss(y=1, f(x))$")
plt.grid()
plt.legend();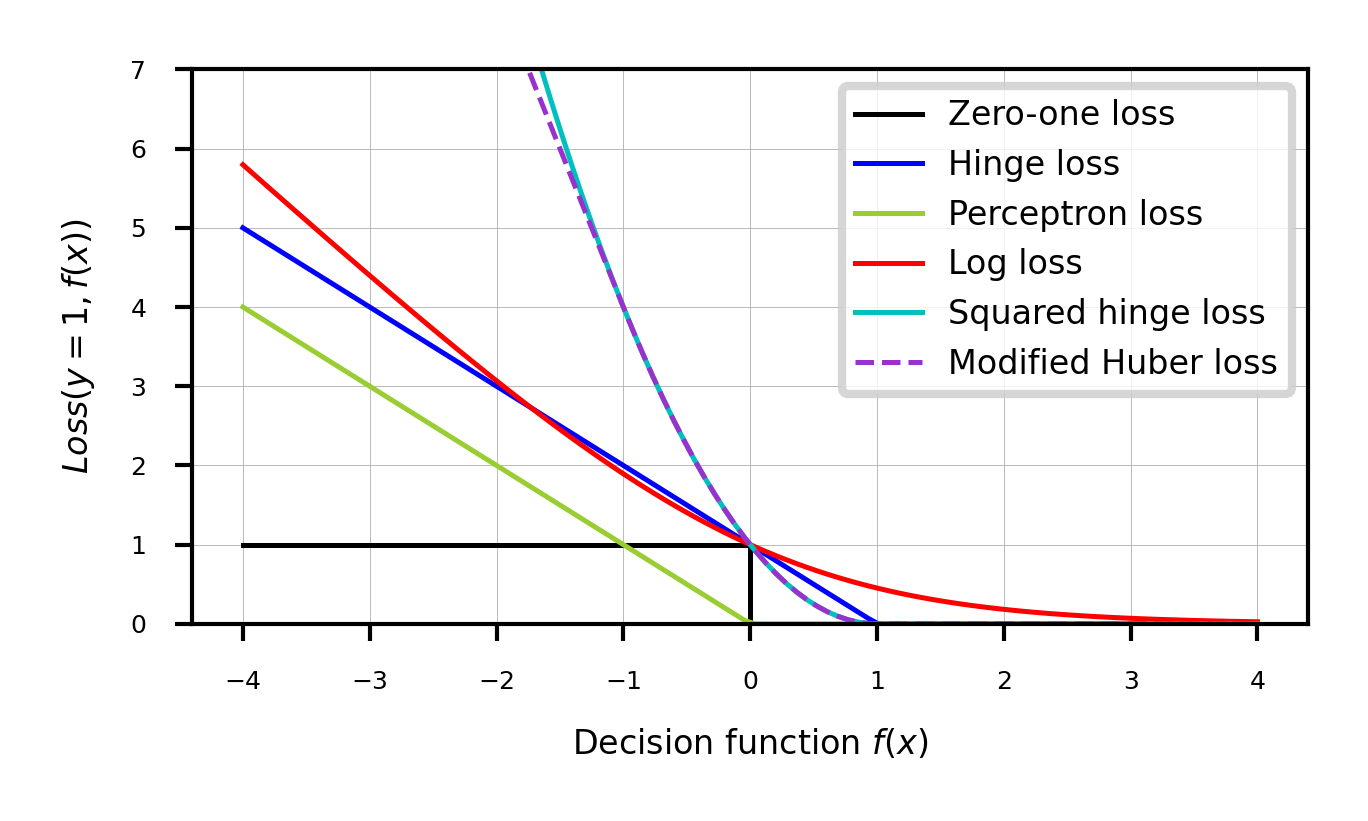
Perceptron¶
Represents a single neuron (node) with inputs , a bias , and output
Each connection has a (synaptic) weight . The node outputs
The activation function (neuron output) is 1 if , -1 otherwise
Idea: Update synapses only on misclassification, correct output by exactly
Weights can be learned with (stochastic) gradient descent and Hinge(0) loss
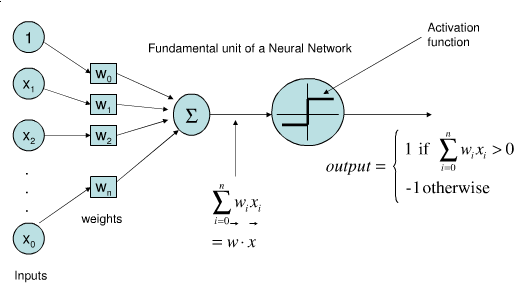
Linear Models for multiclass classification¶
one-vs-rest (aka one-vs-all)¶
Learn a binary model for each class vs. all other classes
Create as many binary models as there are classes
Source
from sklearn.datasets import make_blobs
X, y = make_blobs(random_state=42)
linear_svm = LinearSVC().fit(X, y)
#plt.rcParams["figure.figsize"] = (7*fig_scale,5*fig_scale)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, s=10*fig_scale)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color, lw=2*fig_scale)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1',
'Line class 2'], loc=(1.01, 0.3));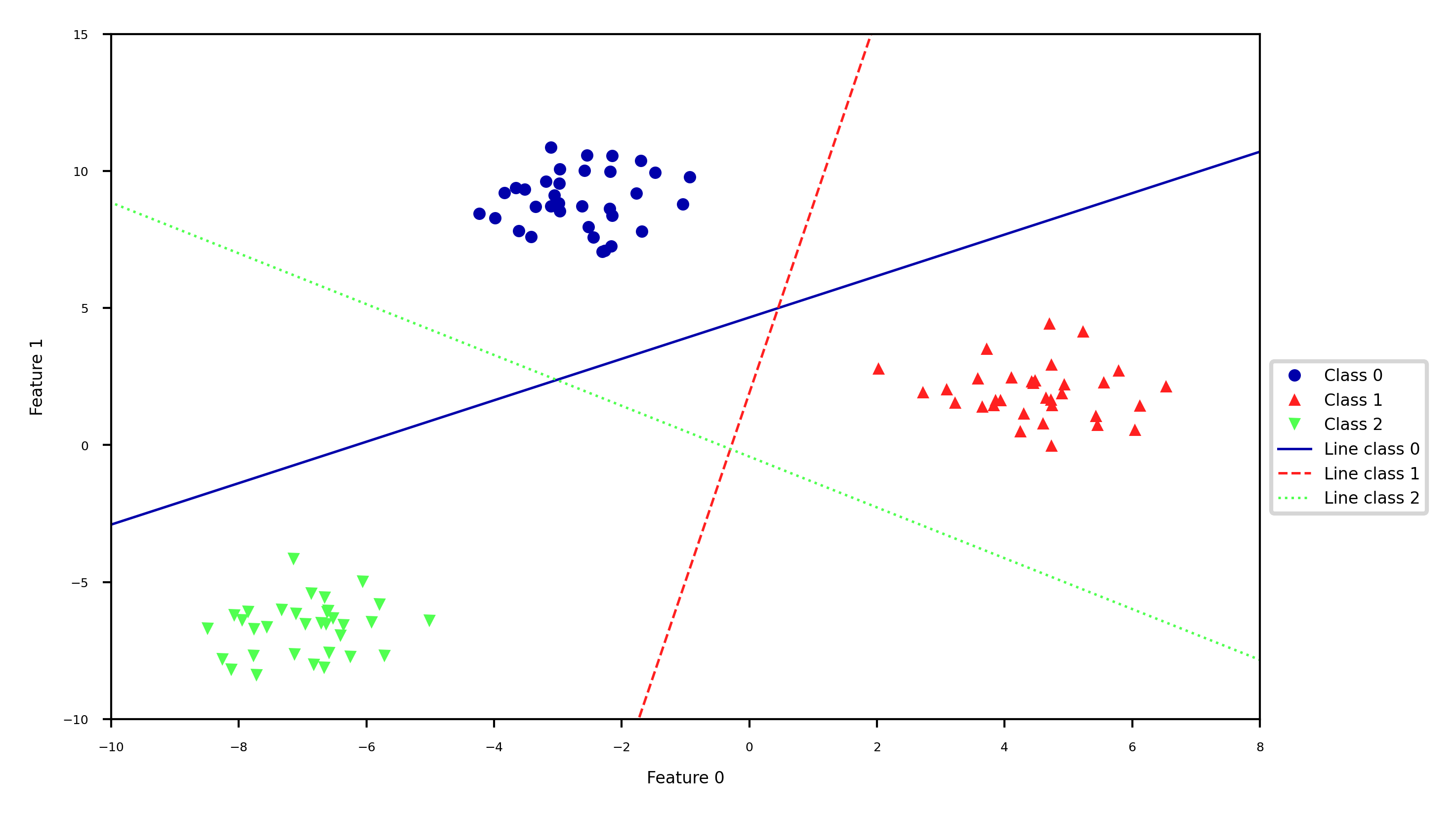
Every binary classifiers makes a prediction, the one with the highest score (>0) wins
Source
mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=0.3)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, s=10*fig_scale)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color, lw=2*fig_scale)
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1',
'Line class 2'], loc=(1.01, 0.3))
plt.xlabel("Feature 0")
plt.ylabel("Feature 1");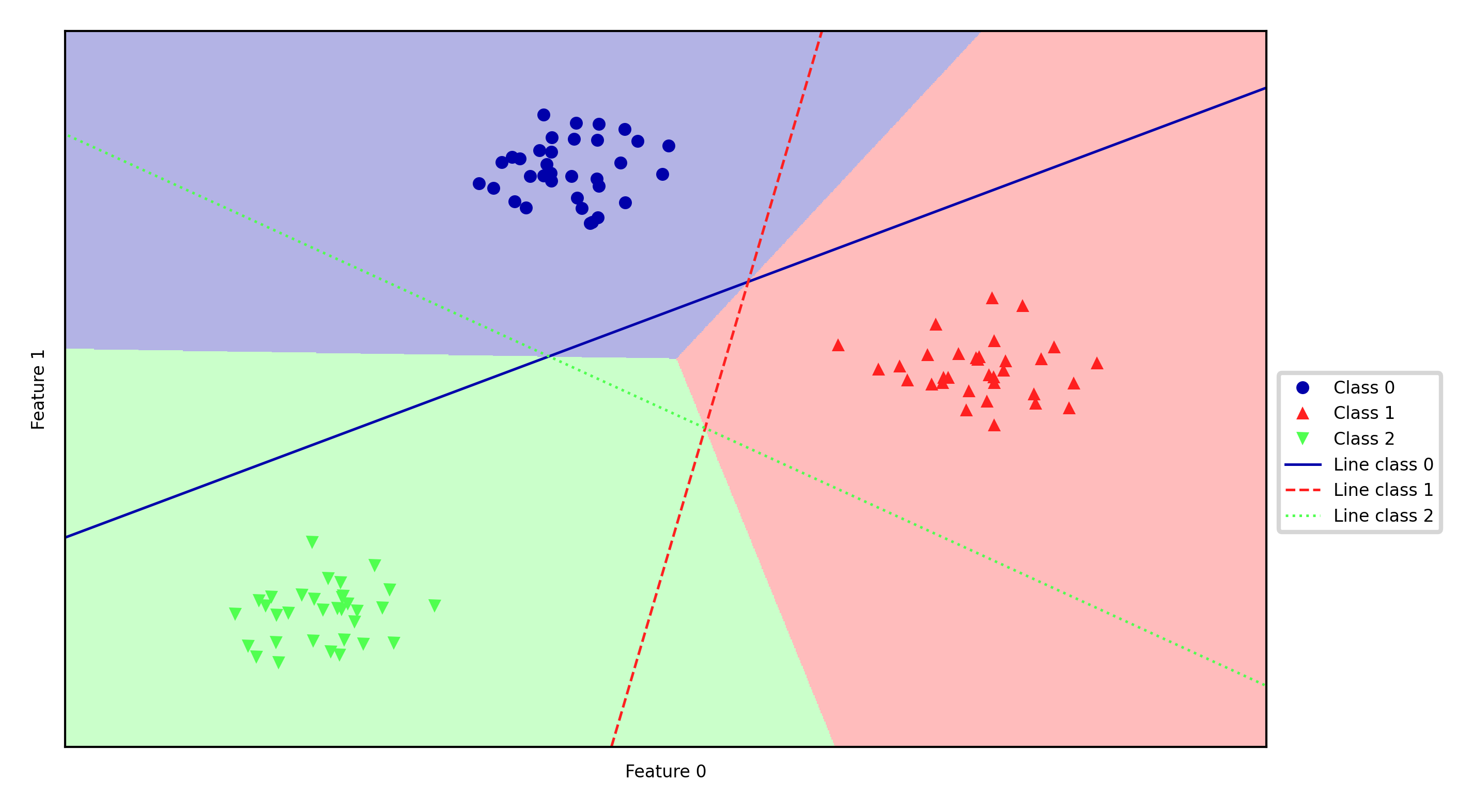
one-vs-one¶
An alternative is to learn a binary model for every combination of two classes
For classes, this results in binary models
Each point is classified according to a majority vote amongst all models
Can also be a ‘soft vote’: sum up the probabilities (or decision values) for all models. The class with the highest sum wins.
Requires more models than one-vs-rest, but training each one is faster
Only the examples of 2 classes are included in the training data
Recommended for algorithms than learn well on small datasets
Especially SVMs and Gaussian Processes
Source
#%%HTML
#<style>
#td {font-size: 16px}
#th {font-size: 16px}
#.rendered_html table, .rendered_html td, .rendered_html th {
# font-size: 16px;
#}
#</style>Linear models overview¶
| Name | Representation | Loss function | Optimization | Regularization |
|---|---|---|---|---|
| Least squares | Linear function (R) | SSE | CFS or SGD | None |
| Ridge | Linear function (R) | SSE + L2 | CFS or SGD | L2 strength () |
| Lasso | Linear function (R) | SSE + L1 | Coordinate descent | L1 strength () |
| Elastic-Net | Linear function (R) | SSE + L1 + L2 | Coordinate descent | , L1 ratio () |
| SGDRegressor | Linear function (R) | SSE, Huber, -ins,... + L1/L2 | SGD | L1/L2, |
| Logistic regression | Linear function (C) | Log + L1/L2 | SGD, coordinate descent,... | L1/L2, |
| Ridge classification | Linear function (C) | SSE + L2 | CFS or SGD | L2 strength () |
| Linear SVM | Support Vectors | Hinge(1) | Quadratic programming or SGD | Cost (C) |
| Kernelized SVM | Support Vectors | Hinge(1) | Quadratic programming or SGD | Cost (C), ,... |
| Least Squares SVM | Support Vectors | Squared Hinge | Linear equations or SGD | Cost (C) |
| Perceptron | Linear function (C) | Hinge(0) | SGD | None |
| SGDClassifier | Linear function (C) | Log, (Sq.) Hinge, Mod. Huber,... | SGD | L1/L2, |
SSE: Sum of Squared Errors
CFS: Closed-form solution
SGD: (Stochastic) Gradient Descent and variants
(R)egression, (C)lassification
Summary¶
Linear models
Good for very large datasets (scalable)
Good for very high-dimensional data (not for low-dimensional data)
Can be used to fit non-linear or low-dim patterns as well (see later)
Preprocessing: e.g. Polynomial or Poisson transformations
Generalized linear models (kernelization)
Regularization is important. Tune the regularization strength ()
Ridge (L2): Good fit, sometimes sensitive to outliers
Lasso (L1): Sparse models: fewer features, more interpretable, faster
Elastic-Net: Trade-off between both, e.g. for correlated features
Most can be solved by different optimizers (solvers)
Closed form solutions or quadratic/linear solvers for smaller datasets
Gradient descent variants (SGD,CD,SAG,CG,...) for larger ones
Multi-class classification can be done using a one-vs-all approach