# General imports
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as pltMachine Learning in Python¶
Joaquin Vanschoren, Eindhoven University of Technology
Why Python?¶
Many data-heavy applications are now developed in Python
Highly readable, less complexity, fast prototyping
Easy to offload number crunching to underlying C/Fortran/...
Easy to install and import many rich libraries
numpy: efficient data structures
scipy: fast numerical recipes
matplotlib: high-quality graphs
scikit-learn: machine learning algorithms
tensorflow: neural networks
...
Numpy, Scipy, Matplotlib¶
We’ll illustrate these with a practical example
Many good tutorials online
from scipy.stats import gamma
np.random.seed(3) # to reproduce the data
def gen_web_traffic_data():
'''
This function generates some fake data that first shows a weekly pattern
for a couple weeks before it grows exponentially.
'''
# 31 days, 24 hours
x = np.arange(1, 31*24)
# Sine wave with weekly rhythm + noise + exponential increase
y = np.array(200*(np.sin(2*np.pi*x/(7*24))), dtype=np.float32)
y += gamma.rvs(15, loc=0, scale=100, size=len(x))
y += 2 * np.exp(x/100.0)
y = np.ma.array(y, mask=[y<0])
return x, y
def plot_web_traffic(x, y, models=None, mx=None, ymax=None):
'''
Plot the web traffic (y) over time (x).
If models is given, it is expected to be a list fitted models,
which will be plotted as well (used later).
'''
plt.figure(figsize=(12,6), dpi=300) # width and height of the plot in inches
plt.scatter(x, y, s=10)
plt.xlabel("Time")
plt.ylabel("Hits/hour")
plt.xticks([w*7*24 for w in range(20)],
['week %i' %w for w in range(20)])
if models:
colors = ['g', 'r', 'm', 'b', 'k']
linestyles = ['-', '-.', '--', ':', '-']
if mx is None:
mx = np.linspace(0, x[-1], 1000)
for model, style, color in zip(models, linestyles, colors):
plt.plot(mx, model(mx), linestyle=style, linewidth=2, c=color)
plt.legend(["d=%i" % m.order for m in models], loc="upper left")
plt.autoscale()
if ymax:
plt.ylim(ymax=ymax)
plt.grid()
plt.ylim(ymin=0)Example: Modelling web traffic¶
We generate some artificial data to mimic web traffic data
E.g. website visits, tweets with certain hashtag,...
Weekly rhythm + noise + exponential increase
x, y = gen_web_traffic_data()
plot_web_traffic(x, y)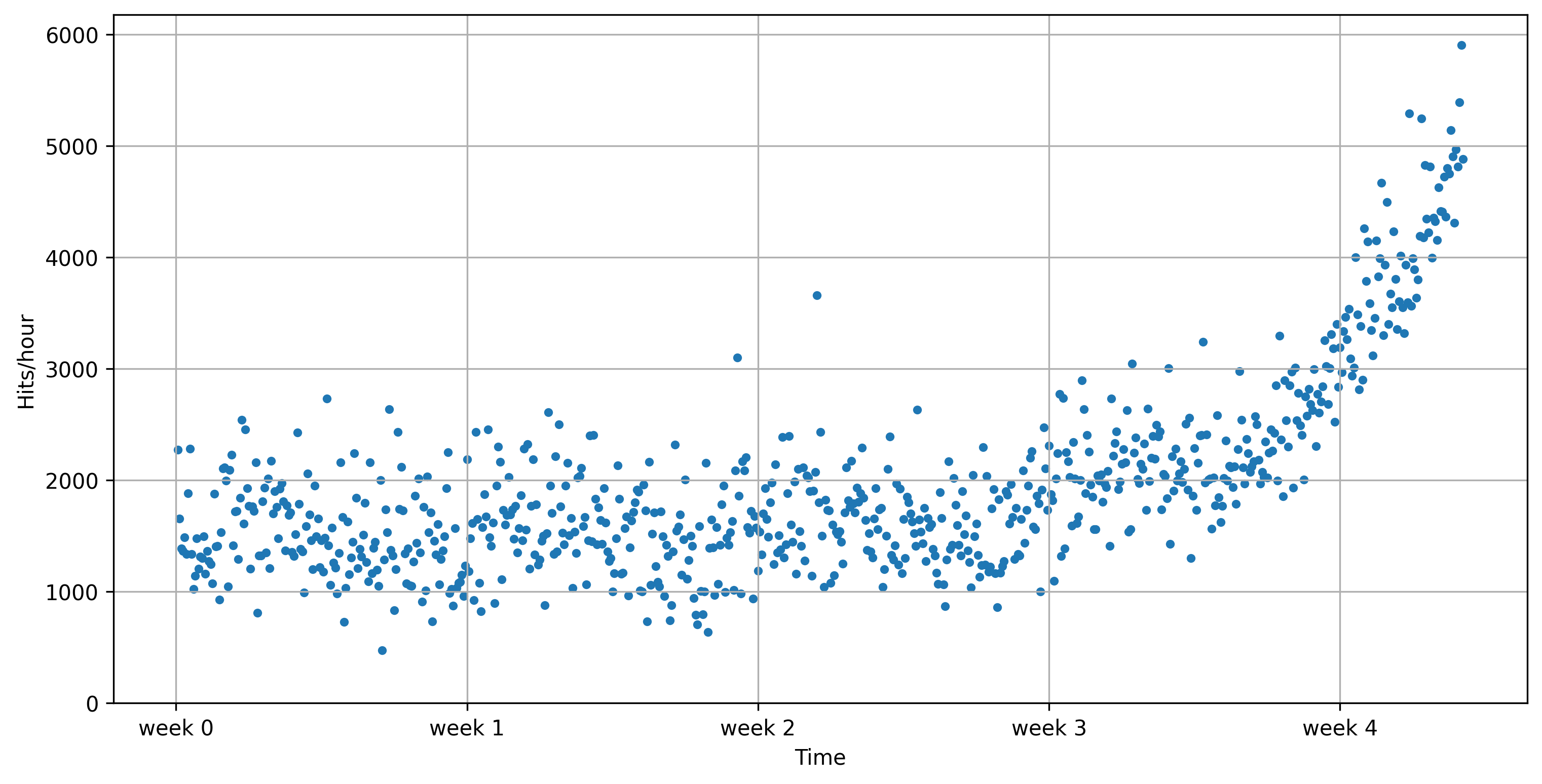
Use numpy to fit some polynomial lines¶
polyfitfits a polynomial of degree dpoly1devaluates the function using the learned coefficientsPlot with matplotlib
f2 = np.poly1d(np.polyfit(x, y, 2))
f10 = np.poly1d(np.polyfit(x, y, 10))
f50 = np.poly1d(np.polyfit(x, y, 50))
mx = np.linspace(0, x[-1], 1000)
plt.plot(mx, f2(mx))f2 = np.poly1d(np.polyfit(x, y, 2))
f10 = np.poly1d(np.polyfit(x, y, 10))
f50 = np.poly1d(np.polyfit(x, y, 50))
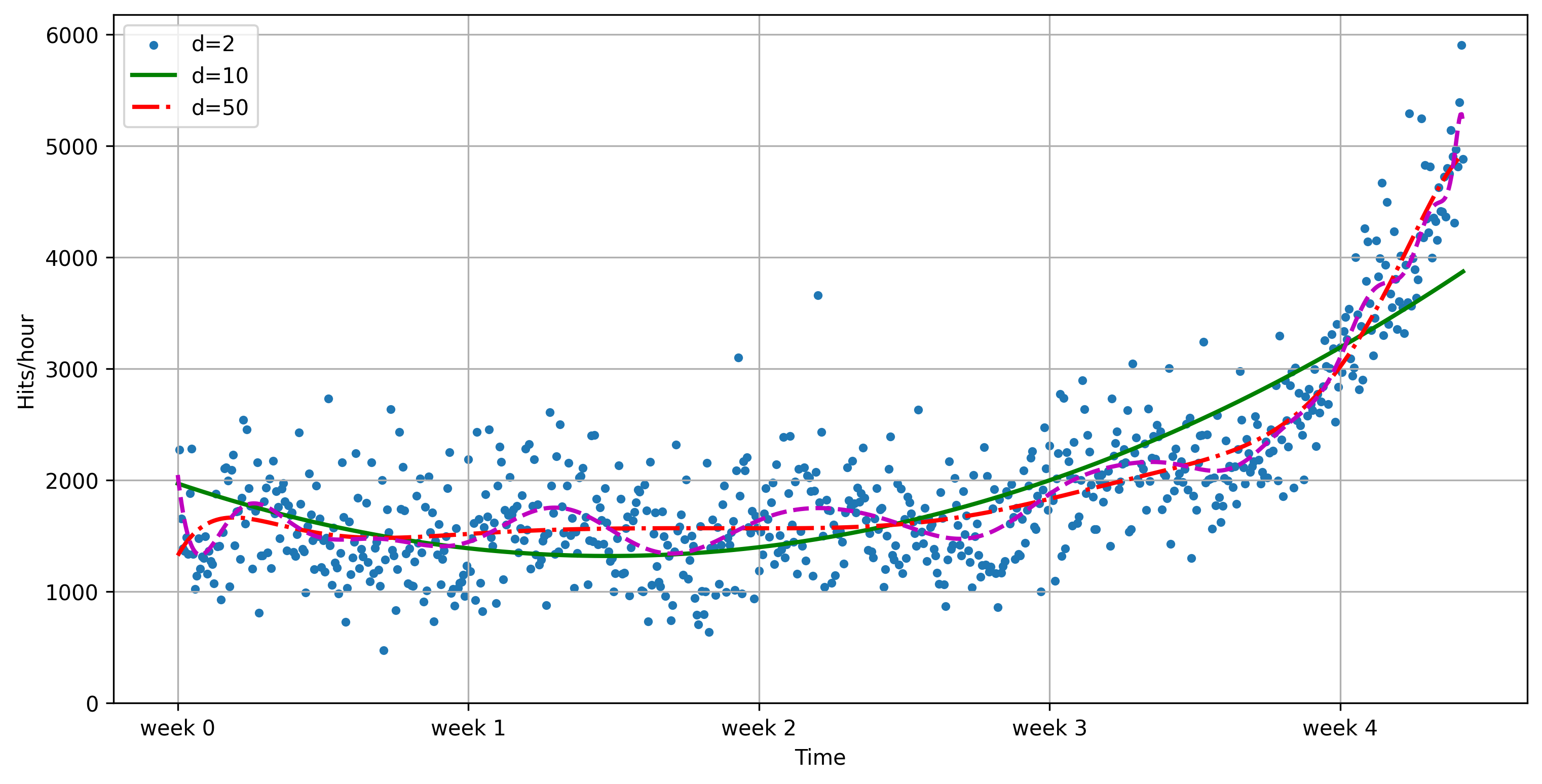
plot_web_traffic(x, y, [f2,f10,f50])/Users/jvanscho/miniforge3/lib/python3.9/site-packages/IPython/core/interactiveshell.py:3457: RankWarning: Polyfit may be poorly conditioned
exec(code_obj, self.user_global_ns, self.user_ns)
Evaluate¶
Using root mean squared error:
The degree of the polynomial needs to be tuned to the data
Predictions don’t look great. We need more sophisticated methods.
import ipywidgets as widgets
from ipywidgets import interact, interact_manual
mx=np.linspace(0, 6 * 7 * 24, 100)
def error(f, x, y):
return np.sqrt(np.sum((f(x)-y)**2))
@interact
def play_with_degree(degree=(1,30,2)):
f = np.poly1d(np.polyfit(x, y, degree))
plot_web_traffic(x, y, [f], mx=mx, ymax=10000)
print("Training error for d=%i: %f" % (f.order, error(f, x, y)))scikit-learn¶
One of the most prominent Python libraries for machine learning:
Contains many state-of-the-art machine learning algorithms
Builds on numpy (fast), implements advanced techniques
Wide range of evaluation measures and techniques
Offers comprehensive documentation about each algorithm
Widely used, and a wealth of tutorials and code snippets are available
Works well with numpy, scipy, pandas, matplotlib,...
Note: We’ll repeat most of the material below in the lectures and labs on model selection and data preprocessing, but it’s still very useful to study it beforehand.
Supervised learning:
Linear models (Ridge, Lasso, Elastic Net, ...)
Support Vector Machines
Tree-based methods (Classification/Regression Trees, Random Forests,...)
Nearest neighbors
Neural networks
Gaussian Processes
Feature selection
Unsupervised learning:
Clustering (KMeans, ...)
Matrix Decomposition (PCA, ...)
Manifold Learning (Embeddings)
Density estimation
Outlier detection
Model selection and evaluation:
Cross-validation
Grid-search
Lots of metrics
Data import¶
Multiple options:
A few toy datasets are included in
sklearn.datasetsImport 1000s of datasets via
sklearn.datasets.fetch_openmlYou can import data files (CSV) with
pandasornumpy
from sklearn.datasets import load_iris, fetch_openml
iris_data = load_iris()
dating_data = fetch_openml(name="SpeedDating")from sklearn.datasets import load_iris, fetch_openml
iris_data = load_iris()
dating_data = fetch_openml("SpeedDating", version=1)These will return a Bunch object (similar to a dict)
print("Keys of iris_dataset: {}".format(iris_dataset.keys()))
print(iris_dataset['DESCR'][:193] + "\n...")print("Keys of iris_dataset: {}".format(iris_data.keys()))
print(iris_data['DESCR'][:193] + "\n...")Keys of iris_dataset: dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])
.. _iris_dataset:
Iris plants dataset
--------------------
**Data Set Characteristics:**
:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, pre
...
Targets (classes) and features are lists of strings
Data and target values are always numeric (ndarrays)
print("Targets: {}".format(iris_data['target_names']))
print("Features: {}".format(iris_data['feature_names']))
print("Shape of data: {}".format(iris_data['data'].shape))
print("First 5 rows:\n{}".format(iris_data['data'][:5]))
print("Targets:\n{}".format(iris_data['target']))print("Targets: {}".format(iris_data['target_names']))
print("Features: {}".format(iris_data['feature_names']))
print("Shape of data: {}".format(iris_data['data'].shape))
print("First 5 rows:\n{}".format(iris_data['data'][:5]))
print("Targets:\n{}".format(iris_data['target']))Targets: ['setosa' 'versicolor' 'virginica']
Features: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Shape of data: (150, 4)
First 5 rows:
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
Targets:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
Building models¶
All scikitlearn estimators follow the same interface
class SupervisedEstimator(...):
def __init__(self, hyperparam, ...):
def fit(self, X, y): # Fit/model the training data
... # given data X and targets y
return self
def predict(self, X): # Make predictions
... # on unseen data X
return y_pred
def score(self, X, y): # Predict and compare to true
... # labels y
return scoreTraining and testing data¶
To evaluate our classifier, we need to test it on unseen data.train_test_split: splits data randomly in 75% training and 25% test data.
X_train, X_test, y_train, y_test = train_test_split(
iris_data['data'], iris_data['target'], random_state=0)from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
iris_data['data'], iris_data['target'],
random_state=0)
print("X_train shape: {}".format(X_train.shape))
print("y_train shape: {}".format(y_train.shape))
print("X_test shape: {}".format(X_test.shape))
print("y_test shape: {}".format(y_test.shape))X_train shape: (112, 4)
y_train shape: (112,)
X_test shape: (38, 4)
y_test shape: (38,)
Fitting a model¶
The first model we’ll build is a k-Nearest Neighbor classifier.
kNN is included in sklearn.neighbors, so let’s build our first model
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)KNeighborsClassifier(n_neighbors=1)Making predictions¶
Let’s create a new example and ask the kNN model to classify it
X_new = np.array([[5, 2.9, 1, 0.2]])
prediction = knn.predict(X_new)
class_name = iris_data['target_names'][prediction]X_new = np.array([[5, 2.9, 1, 0.2]])
prediction = knn.predict(X_new)
print("Prediction: {}".format(prediction))
print("Predicted target name: {}".format(
iris_data['target_names'][prediction]))Prediction: [0]
Predicted target name: ['setosa']
Evaluating the model¶
Feeding all test examples to the model yields all predictions
y_pred = knn.predict(X_test)y_pred = knn.predict(X_test)
print("Test set predictions:\n {}".format(y_pred))Test set predictions:
[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0
2]
The score function computes the percentage of correct predictions
knn.score(X_test, y_test)print("Score: {:.2f}".format(knn.score(X_test, y_test) ))Score: 0.97
Cross-validation¶
More stable, thorough way to estimate generalization performance
k-fold cross-validation (CV): split (randomized) data into k equal-sized parts, called folds
First, fold 1 is the test set, and folds 2-5 comprise the training set
Then, fold 2 is the test set, folds 1,3,4,5 comprise the training set
Compute k evaluation scores, aggregate afterwards (e.g. take the mean)
Cross-validation in scikit-learn¶
cross_val_scorefunction with learner, training data, labelsReturns list of all scores
Does 3-fold CV by default, can be changed via
cvhyperparameterDefault scoring measures are accuracy (classification) or (regression)
Even though models are built internally, they are not returned
knn = KNeighborsClassifier(n_neighbors=1)
scores = cross_val_score(knn, iris.data, iris.target, cv=5)
print("Cross-validation scores: {}".format(scores))
print("Average cross-validation score: {:.2f}".format(scores.mean()))
print("Variance in cross-validation score: {:.4f}".format(np.var(scores)))from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
iris = load_iris()
knn = KNeighborsClassifier(n_neighbors=1)
scores = cross_val_score(knn, iris.data, iris.target)
print("Cross-validation scores: {}".format(scores))
print("Average cross-validation score: {:.2f}".format(scores.mean()))
print("Variance in cross-validation score: {:.4f}".format(np.var(scores)))Cross-validation scores: [0.96666667 0.96666667 0.93333333 0.93333333 1. ]
Average cross-validation score: 0.96
Variance in cross-validation score: 0.0006
More variants¶
Stratified cross-validation: for inbalanced datasets
Leave-one-out cross-validation: for very small datasets
Shuffle-Split cross-validation: whenever you need to shuffle the data first
Repeated cross-validation: more trustworthy, but more expensive
Cross-validation with groups: Whenever your data contains non-independent datapoints, e.g. data points from the same patient
Bootstrapping: sampling with replacement, for extracting statistical properties
Avoid data leakage¶
Simply taking the best performing model based on cross-validation performance yields optimistic results
We’ve already used the test data to evaluate each model!
Hence, we don’t have an independent test set to evaluate these hyperparameter settings
Information ‘leaks’ from test set into the final model
Solution: Set aside part of the training data to evaluate the hyperparameter settings
Select best model on validation set
Rebuild the model on the training+validation set
Evaluate optimal model on the test set
Pipelines¶
Many learning algorithms are greatly affected by how you represent the training data
Examples: Scaling, numeric/categorical values, missing values, feature selection/construction
We typically need chain together different algorithms
Many preprocessing steps
Possibly many models
This is called a pipeline (or workflow)
The best way to represent data depends not only on the semantics of the data, but also on the kind of model you are using.
Example: Speed dating data¶
Data collected from speed dating events
Could also be collected from dating website or app
Real-world data:
Different numeric scales
Missing values
Likely irrelevant features
Different types: Numeric, categorical,...
Input errors (e.g. ‘lawyer’ vs ‘Lawyer’)
dating_data = fetch_openml("SpeedDating")dating_data = fetch_openml("SpeedDating", version=1)Scaling¶
When the features have different scales (their values range between very different minimum and maximum values), one feature will overpower the others. Several scaling techniques are available to solve this:
StandardScalerrescales all features to mean=0 and variance=1Does not ensure and min/max value
RobustScaleruses the median and quartilesMedian m: half of the values < m, half > m
Lower Quartile lq: 1/4 of values < lq
Upper Quartile uq: 1/4 of values > uq
Ignores outliers, brings all features to same scale
MinMaxScalerbrings all feature values between 0 and 1Normalizerscales data such that the feature vector has Euclidean length 1Projects data to the unit circle
Used when only the direction/angle of the data matters
Applying scaling transformations¶
Lets apply a scaling transformation manually, then use it to train a learning algorithm
First, split the data in training and test set
Next, we
fitthe preprocessor on the training dataThis computes the necessary transformation parameters
For
MinMaxScaler, these are the min/max values for every feature
After fitting, we can
transformthe training and test data
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)Missing value imputation¶
Many sci-kit learn algorithms cannot handle missing value
Imputerreplaces specific valuesmissing_values(default ‘NaN’) placeholder for the missing valuestrategy:mean, replace using the mean along the axismedian, replace using the median along the axismost_frequent, replace using the most frequent value
Many more advanced techniques exist, but not yet in scikit-learn
e.g. low rank approximations (uses matrix factorization)
imp = Imputer(missing_values='NaN', strategy='mean', axis=0)
imp.fit_transform(X1_train)Feature encoding¶
scikit-learn classifiers only handle numeric data. If your features are categorical, you need to encode them first
LabelEncodersimply replaces each value with an integer valueOneHotEncoderconverts a feature of values to binary featuresProvide
categoriesas array or set to ‘auto’
X_enc = OneHotEncoder(categories='auto').fit_transform(X)
ColumnTransformercan apply different transformers to different featuresTransformers can be pipelines doing multiple things
numeric_features = ['age', 'pref_o_attractive']
numeric_transformer = Pipeline(steps=[
('imputer', SimpleImputer(strategy='median')),
('scaler', StandardScaler())])
categorical_features = ['gender', 'd_d_age', 'field']
categorical_transformer = Pipeline(steps=[
('imputer', SimpleImputer(strategy='constant', fill_value='missing')),
('onehot', OneHotEncoder(handle_unknown='ignore'))])
preprocessor = ColumnTransformer(
transformers=[
('num', numeric_transformer, numeric_features),
('cat', categorical_transformer, categorical_features)])Building Pipelines¶
In scikit-learn, a
pipelinecombines multiple processing steps in a single estimatorAll but the last step should be transformer (have a
transformmethod)The last step can be a transformer too (e.g. Scaler+PCA)
It has a
fit,predict, andscoremethod, just like any other learning algorithmPipelines are built as a list of steps, which are (name, algorithm) tuples
The name can be anything you want, but can’t contain
'__'We use
'__'to refer to the hyperparameters, e.g.svm__C
Let’s build, train, and score a
MinMaxScaler+LinearSVCpipeline:
pipe = Pipeline([("scaler", MinMaxScaler()), ("svm", LinearSVC())])
pipe.fit(X_train, y_train).score(X_test, y_test)from sklearn.pipeline import Pipeline
from sklearn.preprocessing import MinMaxScaler
from sklearn.svm import LinearSVC
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
pipe = Pipeline([("scaler", MinMaxScaler()), ("svm", LinearSVC())])
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,
random_state=1)
pipe.fit(X_train, y_train)
print("Test score: {:.2f}".format(pipe.score(X_test, y_test)))Test score: 0.97
Now with cross-validation:
scores = cross_val_score(pipe, cancer.data, cancer.target)from sklearn.model_selection import cross_val_score
scores = cross_val_score(pipe, cancer.data, cancer.target)
print("Cross-validation scores: {}".format(scores))
print("Average cross-validation score: {:.2f}".format(scores.mean()))Cross-validation scores: [0.98245614 0.97368421 0.96491228 0.96491228 0.99115044]
Average cross-validation score: 0.98
We can retrieve the trained SVM by querying the right step indices
pipe.steps[1][1]pipe.fit(X_train, y_train)
print("SVM component: {}".format(pipe.steps[1][1]))SVM component: LinearSVC()
Or we can use the
named_stepsdictionary
pipe.named_steps['svm']print("SVM component: {}".format(pipe.named_steps['svm']))SVM component: LinearSVC()
When you don’t need specific names for specific steps, you can use
make_pipelineAssigns names to steps automatically
pipe_short = make_pipeline(MinMaxScaler(), LinearSVC(C=100))
print("Pipeline steps:\n{}".format(pipe_short.steps))from sklearn.pipeline import make_pipeline
# abbreviated syntax
pipe_short = make_pipeline(MinMaxScaler(), LinearSVC(C=100))
print("Pipeline steps:\n{}".format(pipe_short.steps))Pipeline steps:
[('minmaxscaler', MinMaxScaler()), ('linearsvc', LinearSVC(C=100))]
Model selection and Hyperparameter tuning¶
There are many algorithms to choose from
Most algorithms have parameters (hyperparameters) that control model complexity
Now that we know how to evaluate models, we can improve them selecting by
tuningalgorithms for your data
We can basically use any optimization technique to optimize hyperparameters:
Grid search
Random search
More advanced techniques:
Local search
Racing algorithms
Bayesian optimization
Multi-armed bandits
Genetic algorithms
Grid vs Random Search
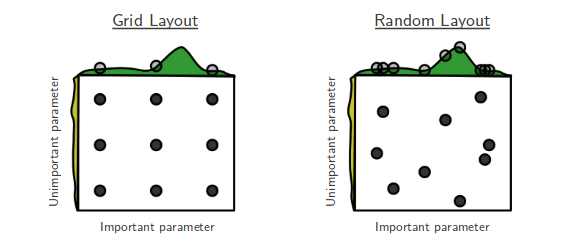
Grid Search¶
For each hyperparameter, create a list of interesting/possible values
E.g. For kNN: k in [1,3,5,7,9,11,33,55,77,99]
E.g. For SVM: C and gamma in [10-10..1010]
Evaluate all possible combinations of hyperparameter values
E.g. using cross-validation
Split the training data into a training and validation set
Select the hyperparameter values yielding the best results on the validation set
Grid search in scikit-learn¶
Create a parameter grid as a dictionary
Keys are parameter names
Values are lists of hyperparameter values
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
print("Parameter grid:\n{}".format(param_grid))param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
print("Parameter grid:\n{}".format(param_grid))Parameter grid:
{'C': [0.001, 0.01, 0.1, 1, 10, 100], 'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
GridSearchCV: like a classifier that uses CV to automatically optimize its hyperparameters internallyInput: (untrained) model, parameter grid, CV procedure
Output: optimized model on given training data
Should only have access to training data
grid_search = GridSearchCV(SVC(), param_grid, cv=5)
grid_search.fit(X_train, y_train)from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
grid_search = GridSearchCV(SVC(), param_grid, cv=5)
X_train, X_test, y_train, y_test = train_test_split(
iris.data, iris.target, random_state=0)
grid_search.fit(X_train, y_train)GridSearchCV(cv=5, estimator=SVC(),
param_grid={'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]})The optimized test score and hyperparameters can easily be retrieved:
grid_search.score(X_test, y_test)
grid_search.best_params_
grid_search.best_score_
grid_search.best_estimator_print("Test set score: {:.2f}".format(grid_search.score(X_test, y_test)))
print("Best parameters: {}".format(grid_search.best_params_))
print("Best cross-validation score: {:.2f}".format(grid_search.best_score_))
print("Best estimator:\n{}".format(grid_search.best_estimator_))Test set score: 0.97
Best parameters: {'C': 10, 'gamma': 0.1}
Best cross-validation score: 0.97
Best estimator:
SVC(C=10, gamma=0.1)
Nested cross-validation¶
Note that we are still using a single split to create the outer test set
We can also use cross-validation here
Nested cross-validation:
Outer loop: split data in training and test sets
Inner loop: run grid search, splitting the training data into train and validation sets
Result is a just a list of scores
There will be multiple optimized models and hyperparameter settings (not returned)
To apply on future data, we need to train
GridSearchCVon all data again
scores = cross_val_score(GridSearchCV(SVC(), param_grid, cv=5),
iris.data, iris.target, cv=5)scores = cross_val_score(GridSearchCV(SVC(), param_grid, cv=5),
iris.data, iris.target, cv=5)
print("Cross-validation scores: ", scores)
print("Mean cross-validation score: ", scores.mean())Cross-validation scores: [0.96666667 1. 0.96666667 0.96666667 1. ]
Mean cross-validation score: 0.9800000000000001
Random Search¶
Grid Search has a few downsides:
Optimizing many hyperparameters creates a combinatorial explosion
You have to predefine a grid, hence you may jump over optimal values
Random Search:
Picks
n_iterrandom parameter valuesScales better, you control the number of iterations
Often works better in practice, too
not all hyperparameters interact strongly
you don’t need to explore all combinations
Executing random search in scikit-learn:
RandomizedSearchCVworks likeGridSearchCVHas
n_iterparameter for the number of iterationsSearch grid can use distributions instead of fixed lists
param_grid = {'C': expon(scale=100),
'gamma': expon(scale=.1)}
random_search = RandomizedSearchCV(SVC(), param_distributions=param_grid,
n_iter=20)
random_search.fit(X_train, y_train)
random_search.best_estimator_from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import expon
param_grid = {'C': expon(scale=100),
'gamma': expon(scale=.1)}
random_search = RandomizedSearchCV(SVC(), param_distributions=param_grid,
n_iter=20)
X_train, X_test, y_train, y_test = train_test_split(
iris.data, iris.target, random_state=0)
random_search.fit(X_train, y_train)
random_search.best_estimator_SVC(C=210.39084256954456, gamma=0.003623016212739808)Using Pipelines in Grid-searches¶
We can use the pipeline as a single estimator in
cross_val_scoreorGridSearchCVTo define a grid, refer to the hyperparameters of the steps
Step
svm, parameterCbecomessvm__C
param_grid = {'svm__C': [0.001, 0.01, 0.1, 1, 10, 100],
'svm__gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
pipe = pipeline.Pipeline([("scaler", MinMaxScaler()), ("svm", SVC(C=100))])
grid = GridSearchCV(pipe, param_grid=param_grid, cv=5)
grid.fit(X_train, y_train)param_grid = {'svm__C': [0.001, 0.01, 0.1, 1, 10, 100],
'svm__gamma': [0.001, 0.01, 0.1, 1, 10, 100]}from sklearn import pipeline
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
pipe = pipeline.Pipeline([("scaler", MinMaxScaler()), ("svm", SVC(C=100))])
grid = GridSearchCV(pipe, param_grid=param_grid, cv=5)
grid.fit(X_train, y_train)
print("Best cross-validation accuracy: {:.2f}".format(grid.best_score_))
print("Test set score: {:.2f}".format(grid.score(X_test, y_test)))
print("Best parameters: {}".format(grid.best_params_))Best cross-validation accuracy: 0.96
Test set score: 0.97
Best parameters: {'svm__C': 1, 'svm__gamma': 10}
Automated Machine Learning¶
Optimizes both the pipeline and all hyperparameters
E.g. auto-sklearn
Drop-in sklearn classifier
Also optimizes pipelines (e.g. feature selection)
Uses OpenML to find good models on similar datasets
Lacks Windows support
automl = autosklearn.classification.AutoSklearnClassifier(
time_left_for_this_task=60, # sec., for entire process
per_run_time_limit=15, # sec., for each model
ml_memory_limit=1024, # MB, memory limit
)
automl.fit(X_train, y_train)