Overview¶
- Neural architectures
- Training neural nets
- Forward pass: Tensor operations
- Backward pass: Backpropagation
- Neural network design:
- Activation functions
- Weight initialization
- Optimizers
- Neural networks in practice
- Model selection
- Early stopping
- Memorization capacity and information bottleneck
- L1/L2 regularization
- Dropout
- Batch normalization
Linear models as a building block¶
- Logistic regression, drawn in a different, neuro-inspired, way
- Linear model: inner product ($z$) of input vector $\mathbf{x}$ and weight vector $\mathbf{w}$, plus bias $w_0$
- Logistic (or sigmoid) function maps the output to a probability in [0,1]
- Uses log loss (cross-entropy) and gradient descent to learn the weights
Basic Architecture¶
- Add one (or more) hidden layers $h$ with $k$ nodes (or units, cells, neurons)
- Every 'neuron' is a tiny function, the network is an arbitrarily complex function
- Weights $w_{i,j}$ between node $i$ and node $j$ form a weight matrix $\mathbf{W}^{(l)}$ per layer $l$
- Every neuron weights the inputs $\mathbf{x}$ and passes it through a non-linear activation function
- Activation functions ($f,g$) can be different per layer, output $\mathbf{a}$ is called activation $$\color{blue}{h(\mathbf{x})} = \color{blue}{\mathbf{a}} = f(\mathbf{z}) = f(\mathbf{W}^{(1)} \color{green}{\mathbf{x}}+\mathbf{w}^{(1)}_0) \quad \quad \color{red}{o(\mathbf{x})} = g(\mathbf{W}^{(2)} \color{blue}{\mathbf{a}}+\mathbf{w}^{(2)}_0)$$
More layers¶
- Add more layers, and more nodes per layer, to make the model more complex
- For simplicity, we don't draw the biases (but remember that they are there)
- In dense (fully-connected) layers, every previous layer node is connected to all nodes
- The output layer can also have multiple nodes (e.g. 1 per class in multi-class classification)
interactive(children=(IntSlider(value=3, description='nr_layers', max=6), IntSlider(value=6, description='nr_n…
Why layers?¶
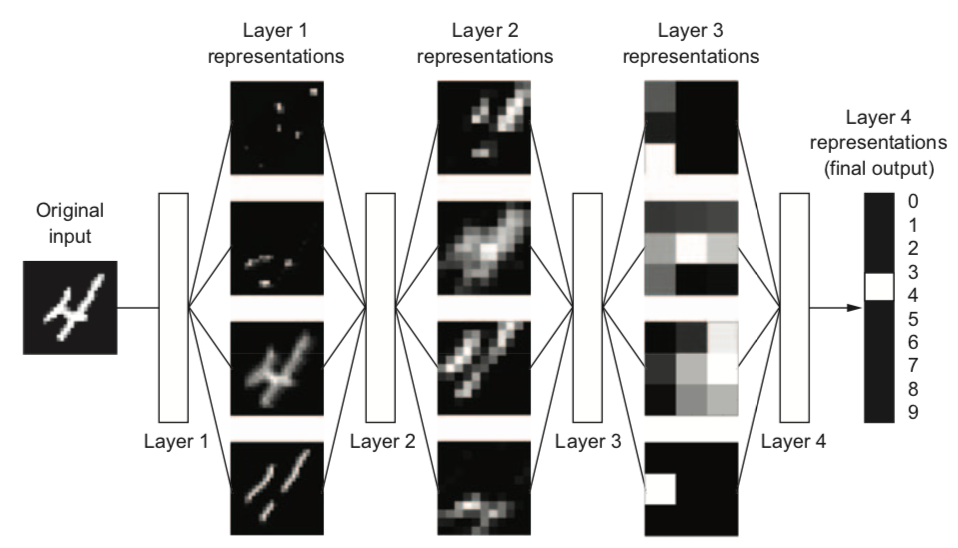
- Each layer acts as a filter and learns a new representation of the data
- Subsequent layers can learn iterative refinements
- Easier that learning a complex relationship in one go
- Example: for image input, each layer yields new (filtered) images
- Can learn multiple mappings at once: weight tensor $\mathit{W}$ yields activation tensor $\mathit{A}$
- From low-level patterns (edges, end-points, ...) to combinations thereof
- Each neuron 'lights up' if certain patterns occur in the input
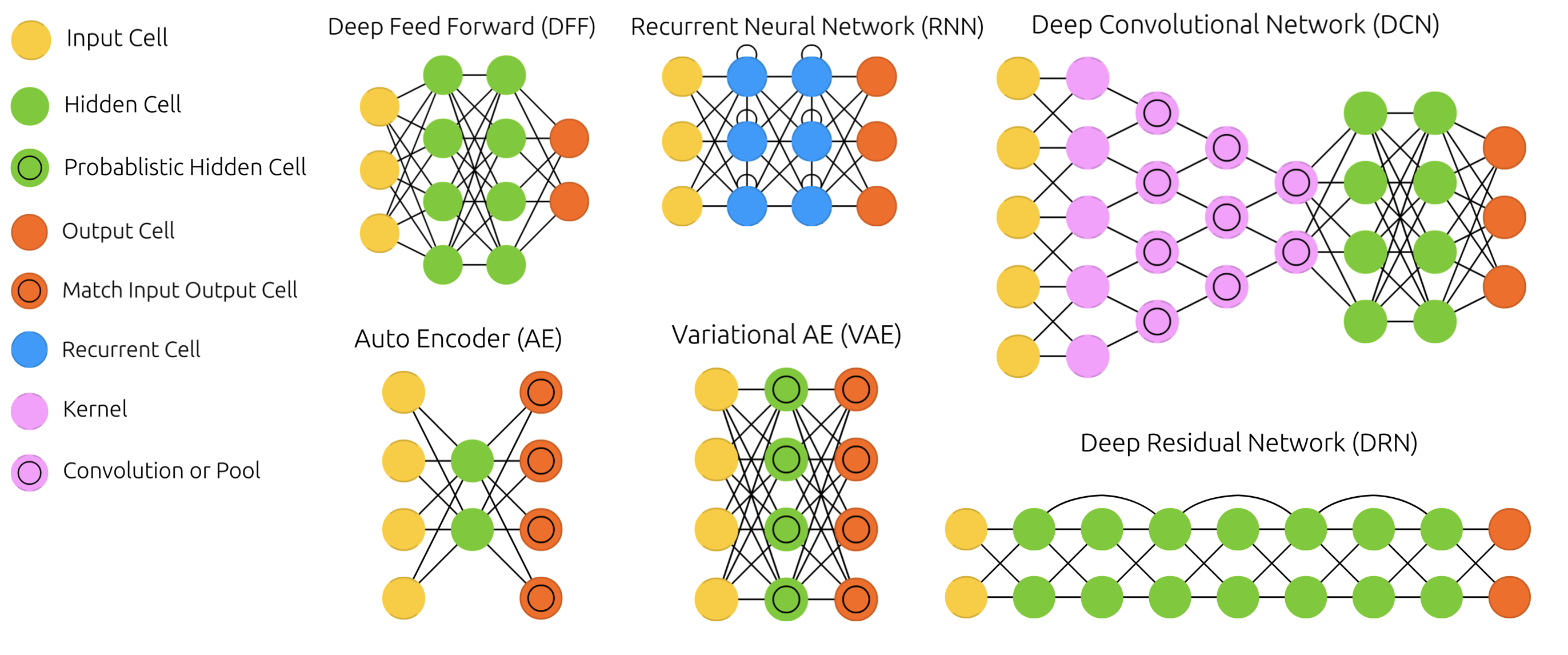
Other architectures¶
- There exist MANY types of networks for many different tasks
- Convolutional nets for image data, Recurrent nets for sequential data,...
- Also used to learn representations (embeddings), generate new images, text,...
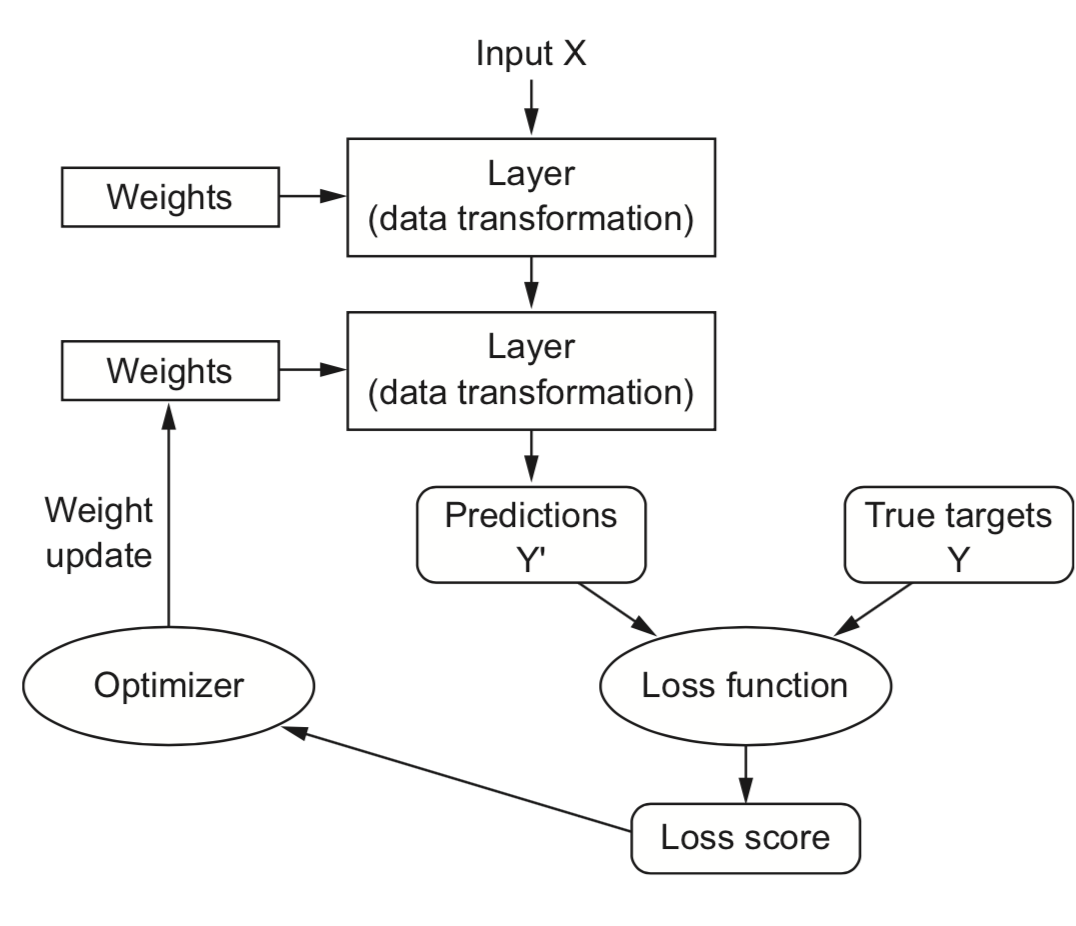
Training Neural Nets¶
- Design the architecture, choose activation functions (e.g. sigmoids)
- Choose a way to initialize the weights (e.g. random initialization)
- Choose a loss function (e.g. log loss) to measure how well the model fits training data
- Choose an optimizer (typically an SGD variant) to update the weights
Mini-batch Stochastic Gradient Descent (recap)¶
- Draw a batch of batch_size training data $\mathbf{X}$ and $\mathbf{y}$
- Forward pass : pass $\mathbf{X}$ though the network to yield predictions $\mathbf{\hat{y}}$
- Compute the loss $\mathcal{L}$ (mismatch between $\mathbf{\hat{y}}$ and $\mathbf{y}$)
- Backward pass : Compute the gradient of the loss with regard to every weight
- Backpropagate the gradients through all the layers
- Update $W$: $W_{(i+1)} = W_{(i)} - \frac{\partial L(x, W_{(i)})}{\partial W} * \eta$
Repeat until n passes (epochs) are made through the entire training set
interactive(children=(IntSlider(value=50, description='iteration', min=1), Output()), _dom_classes=('widget-in…
Forward pass¶
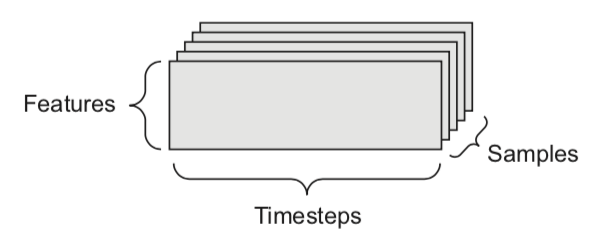
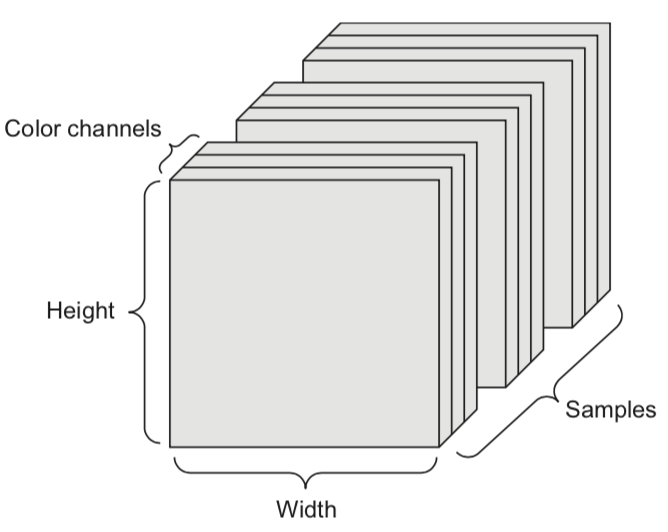
- We can naturally represent the data as tensors
- Numerical n-dimensional array (with n axes)
- 2D tensor: matrix (samples, features)
- 3D tensor: time series (samples, timesteps, features)
- 4D tensor: color images (samples, height, width, channels)
- 5D tensor: video (samples, frames, height, width, channels)
Tensor operations¶
- The operations that the network performs on the data can be reduced to a series of tensor operations
- These are also much easier to run on GPUs
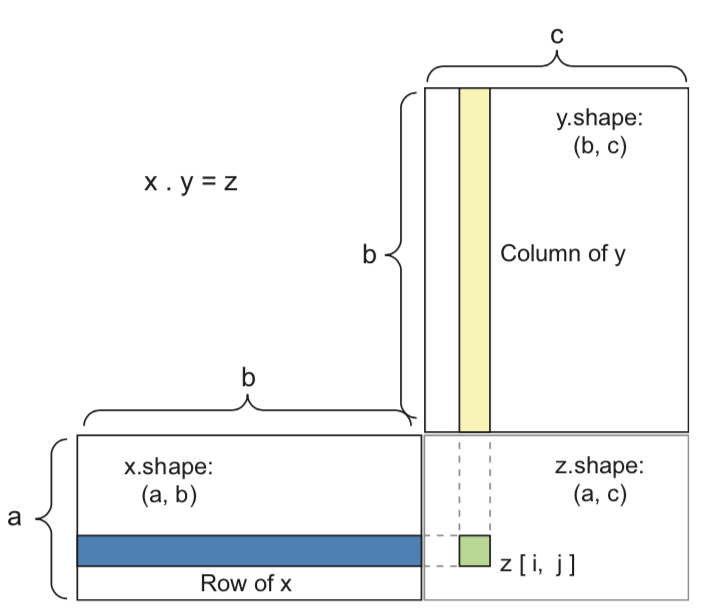
- A dense layer with sigmoid activation, input tensor $\mathbf{X}$, weight tensor $\mathbf{W}$, bias $\mathbf{b}$:
y = sigmoid(np.dot(X, W) + b)
- Tensor dot product for 2D inputs ($a$ samples, $b$ features, $c$ hidden nodes)
Element-wise operations¶
- Activation functions and addition are element-wise operations:
def sigmoid(x):
return 1/(1 + np.exp(-x))
def add(x, y):
return x + y
- Note: if y has a lower dimension than x, it will be broadcasted: axes are added to match the dimensionality, and y is repeated along the new axes
>>> np.array([[1,2],[3,4]]) + np.array([10,20])
array([[11, 22],
[13, 24]])
Backward pass (backpropagation)¶
- For last layer, compute gradient of the loss function $\mathcal{L}$ w.r.t all weights of layer $l$
- Sum up the gradients for all $\mathbf{x}_j$ in minibatch: $\sum_{j} \frac{\partial \mathcal{L}(\mathbf{x}_j,y_j)}{\partial W^{(l)}}$
- Update all weights in a layer at once (with learning rate $\eta$): $W_{(i+1)}^{(l)} = W_{(i)}^{(l)} - \eta \sum_{j} \frac{\partial \mathcal{L}(\mathbf{x}_j,y_j)}{\partial W_{(i)}^{(l)}}$
- Repeat for next layer, iterating backwards (most efficient, avoids redundant calculations)
Backpropagation (example)¶
- Imagine feeding a single data point, output is $\hat{y} = g(z) = g(w_0 + w_1 * a_1 + w_2 * a_2 +... + w_p * a_p)$
- Decrease loss by updating weights:
- Update the weights of last layer to maximize improvement: $w_{i,(new)} = w_{i} - \frac{\partial \mathcal{L}}{\partial w_i} * \eta$
- To compute gradient $\frac{\partial \mathcal{L}}{\partial w_i}$ we need the chain rule: $f(g(x)) = f'(g(x)) * g'(x)$ $$\frac{\partial \mathcal{L}}{\partial w_i} = \color{red}{\frac{\partial \mathcal{L}}{\partial g}} \color{blue}{\frac{\partial \mathcal{g}}{\partial z_0}} \color{green}{\frac{\partial \mathcal{z_0}}{\partial w_i}}$$
- E.g., with $\mathcal{L} = \frac{1}{2}(y-\hat{y})^2$ and sigmoid $\sigma$: $\frac{\partial \mathcal{L}}{\partial w_i} = \color{red}{(y - \hat{y})} * \color{blue}{\sigma'(z_0)} * \color{green}{a_i}$
Backpropagation (2)¶
- Another way to decrease the loss $\mathcal{L}$ is to update the activations $a_i$
- To update $a_i = f(z_i)$, we need to update the weights of the previous layer
- We want to nudge $a_i$ in the right direction by updating $w_{i,j}$: $$\frac{\partial \mathcal{L}}{\partial w_{i,j}} = \frac{\partial \mathcal{L}}{\partial a_i} \frac{\partial a_i}{\partial z_i} \frac{\partial \mathcal{z_i}}{\partial w_{i,j}} = \left( \frac{\partial \mathcal{L}}{\partial g} \frac{\partial \mathcal{g}}{\partial z_0} \frac{\partial \mathcal{z_0}}{\partial a_i} \right) \frac{\partial a_i}{\partial z_i} \frac{\partial \mathcal{z_i}}{\partial w_{i,j}}$$
- We know $\frac{\partial \mathcal{L}}{\partial g}$ and $\frac{\partial \mathcal{g}}{\partial z_0}$ from the previous step, $\frac{\partial \mathcal{z_0}}{\partial a_i} = w_i$, $\frac{\partial a_i}{\partial z_i} = f'$ and $\frac{\partial \mathcal{z_i}}{\partial w_{i,j}} = x_j$
Backpropagation (3)¶
- With multiple output nodes, $\mathcal{L}$ is the sum of all per-output (per-class) losses
- $\frac{\partial \mathcal{L}}{\partial a_i}$ is sum of the gradients for every output
- Per layer, sum up gradients for every point $\mathbf{x}$ in the batch: $\sum_{j} \frac{\partial \mathcal{L}(\mathbf{x}_j,y_j)}{\partial W}$
- Update all weights of every layer $l$
- $W_{(i+1)}^{(l)} = W_{(i)}^{(l)} - \eta \sum_{j} \frac{\partial \mathcal{L}(\mathbf{x}_j,y_j)}{\partial W_{(i)}^{(l)}}$
- Repeat with a new batch of data until loss converges
- Nice animation of the entire process
Backpropagation (summary)¶
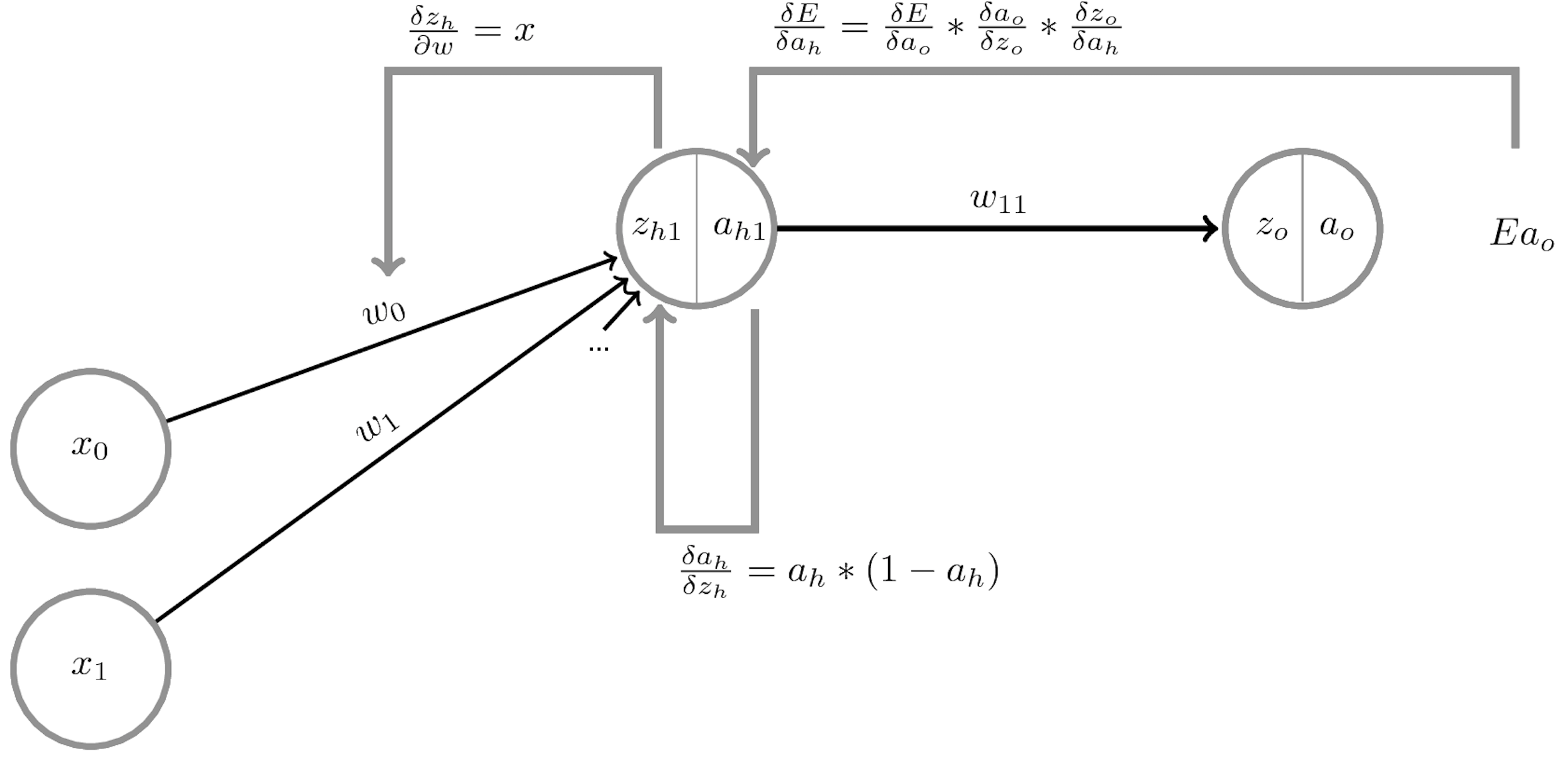
- The network output $a_o$ is defined by the weights $W^{(o)}$ and biases $\mathbf{b}^{(o)}$ of the output layer, and
- The activations of a hidden layer $h_1$ with activation function $a_{h_1}$, weights $W^{(1)}$ and biases $\mathbf{b^{(1)}}$:
- Minimize the loss by SGD. For layer $l$, compute $\frac{\partial \mathcal{L}(a_o(x))}{\partial W_l}$ and $\frac{\partial \mathcal{L}(a_o(x))}{\partial b_{l,i}}$ using the chain rule
- Decomposes into gradient of layer above, gradient of activation function, gradient of layer input:
Activation functions for hidden layers¶
- Sigmoid: $f(z) = \frac{1}{1+e^{-z}}$
- Tanh: $f(z) = \frac{2}{1+e^{-2z}} - 1$
- Activations around 0 are better for gradient descent convergence
- Rectified Linear (ReLU): $f(z) = max(0,z)$
- Less smooth, but much faster (note: not differentiable at 0)
- Leaky ReLU: $f(z) = \begin{cases} 0.01z & z<0 \\ z & otherwise \end{cases}$
interactive(children=(Dropdown(description='function', options=('sigmoid', 'tanh', 'relu', 'leaky_relu'), valu…
Effect of activation functions on the gradient¶
- During gradient descent, the gradient depends on the activation function $a_{h}$: $\frac{\partial \mathcal{L}(a_o)}{\partial W^{(l)}} = \color{red}{\frac{\partial \mathcal{L}(a_o)}{\partial a_{h_l}}} \color{blue}{\frac{\partial a_{h_l}}{\partial z_{h_l}}} \color{green}{\frac{\partial z_{h_l}}{\partial W^{(l)}}}$
- If derivative of the activation function $\color{blue}{\frac{\partial a_{h_l}}{\partial z_{h_l}}}$ is 0, the weights $w_i$ are not updated
- Moreover, the gradients of previous layers will be reduced (vanishing gradient)
- sigmoid, tanh: gradient is very small for large inputs: slow updates
- With ReLU, $\color{blue}{\frac{\partial a_{h_l}}{\partial z_{h_l}}} = 1$ if $z>0$, hence better against vanishing gradients
- Problem: for very negative inputs, the gradient is 0 and may never recover (dying ReLU)
- Leaky ReLU has a small (0.01) gradient there to allow recovery
interactive(children=(Dropdown(description='function', options=('sigmoid', 'tanh', 'relu', 'leaky_relu'), valu…
ReLU vs Tanh¶
- What is the effect of using non-smooth activation functions?
- ReLU produces piecewise-linear boundaries, but allows deeper networks
- Tanh produces smoother decision boundaries, but is slower
interactive(children=(IntSlider(value=2, description='nr_layers', max=4, min=1), Output()), _dom_classes=('wid…
Activation functions for output layer¶
- sigmoid converts output to probability in [0,1]
- For binary classification
- softmax converts all outputs (aka 'logits') to probabilities that sum up to 1
- For multi-class classification ($k$ classes)
- Can cause over-confident models. If so, smooth the labels: $y_{smooth} = (1-\alpha)y + \frac{\alpha}{k}$ $$\text{softmax}(\mathbf{x},i) = \frac{e^{x_i}}{\sum_{j=1}^k e^{x_j}}$$
- For regression, don't use any activation function, let the model learn the exact target
interactive(children=(Dropdown(description='function', options=('sigmoid', 'softmax', 'none'), value='sigmoid'…
Weight initialization¶
- Initializing weights to 0 is bad: all gradients in layer will be identical (symmetry)
- Too small random weights shrink activations to 0 along the layers (vanishing gradient)
- Too large random weights multiply along layers (exploding gradient, zig-zagging)
- Ideal: small random weights + variance of input and output gradients remains the same
- Glorot/Xavier initialization (for tanh): randomly sample from $N(0,\sigma), \sigma = \sqrt{\frac{2}{\text{fan_in + fan_out}}}$
- fan_in: number of input units, fan_out: number of output units
- He initialization (for ReLU): randomly sample from $N(0,\sigma), \sigma = \sqrt{\frac{2}{\text{fan_in}}}$
- Uniform sampling (instead of $N(0,\sigma)$) for deeper networks (w.r.t. vanishing gradients)
- Glorot/Xavier initialization (for tanh): randomly sample from $N(0,\sigma), \sigma = \sqrt{\frac{2}{\text{fan_in + fan_out}}}$
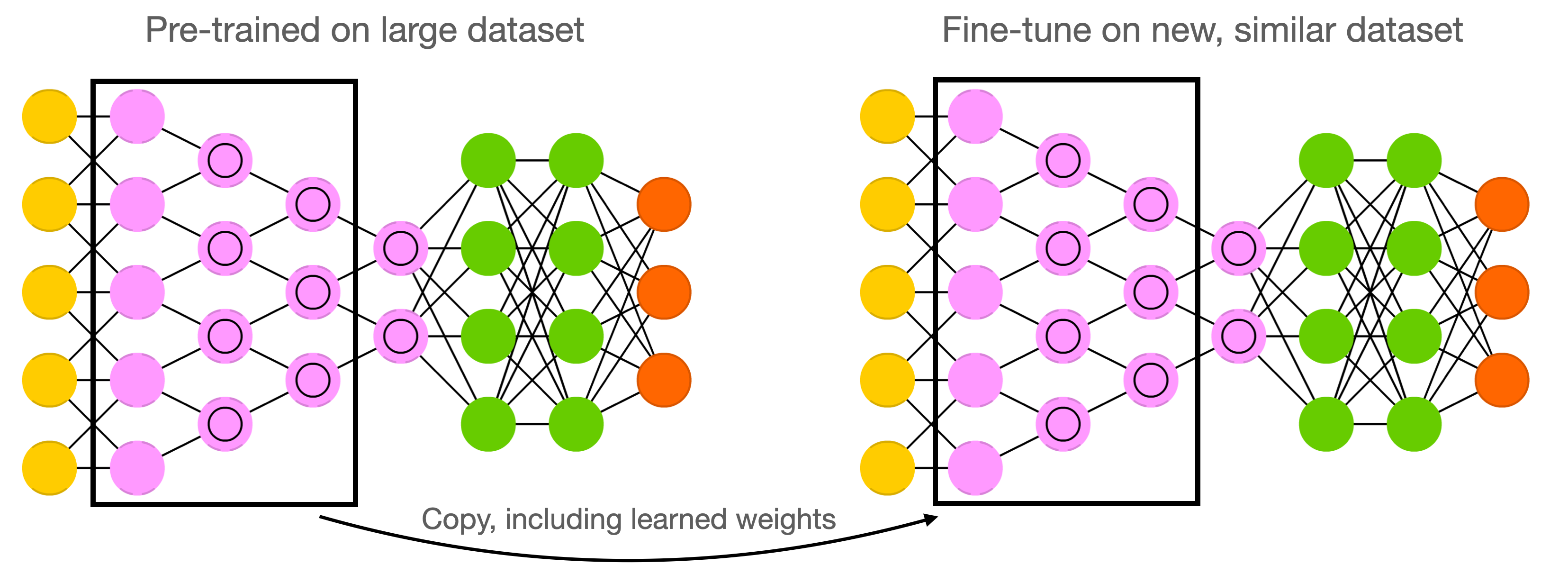
Weight initialization: transfer learning¶
- Instead of starting from scratch, start from weights previously learned from similar tasks
- This is, to a big extent, how humans learn so fast
- Transfer learning: learn weights on task T, transfer them to new network
- Weights can be frozen, or finetuned to the new data
- Only works if the previous task is 'similar' enough
- Meta-learning: learn a good initialization across many related tasks
Optimizers¶
SGD with learning rate schedules¶
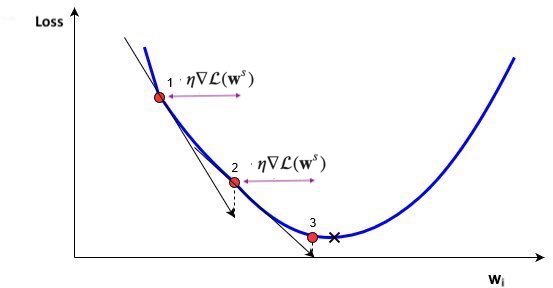
- Using a constant learning $\eta$ rate for weight updates $\mathbf{w}_{(s+1)} = \mathbf{w}_s-\eta\nabla \mathcal{L}(\mathbf{w}_s)$ is not ideal
- Learning rate decay/annealing with decay rate $k$
- E.g. exponential ($\eta_{s+1} = \eta_{s} e^{-ks}$), inverse-time ($\eta_{s+1} = \frac{\eta_{0}}{1+ks}$),...
- Cyclical learning rates
- Change from small to large: hopefully in 'good' region long enough before diverging
- Warm restarts: aggressive decay + reset to initial learning rate
interactive(children=(IntSlider(value=50, description='iterations', min=1), Dropdown(description='optimizer1',…
Momentum¶
- Imagine a ball rolling downhill: accumulates momentum, doesn't exactly follow steepest descent
- Reduces oscillation, follows larger (consistent) gradient of the loss surface
- Adds a velocity vector $\mathbf{v}$ with momentum $\gamma$ (e.g. 0.9, or increase from $\gamma=0.5$ to $\gamma=0.99$) $$\mathbf{w}_{(s+1)} = \mathbf{w}_{(s)} + \mathbf{v}_{(s)} \qquad \text{with} \qquad \color{blue}{\mathbf{v}_{(s)}} = \color{green}{\gamma \mathbf{v}_{(s-1)}} - \color{red}{\eta \nabla \mathcal{L}(\mathbf{w}_{(s)})}$$
- Nesterov momentum: Look where momentum step would bring you, compute gradient there
- Responds faster (and reduces momentum) when the gradient changes $$\color{blue}{\mathbf{v}_{(s)}} = \color{green}{\gamma \mathbf{v}_{(s-1)}} - \color{red}{\eta \nabla \mathcal{L}(\mathbf{w}_{(s)} + \gamma \mathbf{v}_{(s-1)})}$$
Momentum in practice¶
interactive(children=(IntSlider(value=50, description='iterations', min=1), Dropdown(description='optimizer1',…
Adaptive gradients¶
- 'Correct' the learning rate for each $w_i$ based on specific local conditions (layer depth, fan-in,...)
- Adagrad: scale $\eta$ according to squared sum of previous gradients $G_{i,(s)} = \sum_{t=1}^s \mathcal{L}(w_{i,(t)})^2$
- Update rule for $w_i$. Usually $\epsilon=10^{-7}$ (avoids division by 0), $\eta=0.001$. $$w_{i,(s+1)} = w_{i,(s)} - \frac{\eta}{\sqrt{G_{i,(s)}+\epsilon}} \nabla \mathcal{L}(w_{i,(s)})$$
- RMSProp: use moving average of squared gradients $m_{i,(s)} = \gamma m_{i,(s-1)} + (1-\gamma) \nabla \mathcal{L}(w_{i,(s)})^2$
- Avoids that gradients dwindle to 0 as $G_{i,(s)}$ grows. Usually $\gamma=0.9, \eta=0.001$ $$w_{i,(s+1)} = w_{i,(s)}- \frac{\eta}{\sqrt{m_{i,(s)}+\epsilon}} \nabla \mathcal{L}(w_{i,(s)})$$
interactive(children=(IntSlider(value=50, description='iterations', min=1), Dropdown(description='optimizer1',…
Adam (Adaptive moment estimation)¶
Adam: RMSProp + momentum. Adds moving average for gradients as well ($\gamma_2$ = momentum):
- Adds a bias correction to avoid small initial gradients: $\hat{m}_{i,(s)} = \frac{m_{i,(s)}}{1-\gamma}$ and $\hat{g}_{i,(s)} = \frac{g_{i,(s)}}{1-\gamma_2}$ $$g_{i,(s)} = \gamma_2 g_{i,(s-1)} + (1-\gamma_2) \nabla \mathcal{L}(w_{i,(s)})$$ $$w_{i,(s+1)} = w_{i,(s)}- \frac{\eta}{\sqrt{\hat{m}_{i,(s)}+\epsilon}} \hat{g}_{i,(s)}$$
Adamax: Idem, but use max() instead of moving average: $u_{i,(s)} = max(\gamma u_{i,(s-1)}, |\mathcal{L}(w_{i,(s)})|)$ $$w_{i,(s+1)} = w_{i,(s)}- \frac{\eta}{u_{i,(s)}} \hat{g}_{i,(s)}$$
interactive(children=(IntSlider(value=50, description='iterations', min=1), Dropdown(description='optimizer1',…
interactive(children=(IntSlider(value=50, description='iterations', min=1), Output()), _dom_classes=('widget-i…
Neural networks in practice¶
- There are many practical courses on training neural nets. E.g.:
- With TensorFlow: https://www.tensorflow.org/resources/learn-ml
- With PyTorch: fast.ai course, https://pytorch.org/tutorials/
- Here, we'll use Keras, a general API for building neural networks
- Default API for TensorFlow, also has backends for CNTK, Theano
- Focus on key design decisions, evaluation, and regularization
- Running example: Fashion-MNIST
- 28x28 pixel images of 10 classes of fashion items
Building the network¶
- We first build a simple sequential model (no branches)
- Input layer ('input_shape'): a flat vector of 28*28=784 nodes
- We'll see how to properly deal with images later
- Two dense hidden layers: 512 nodes each, ReLU activation
- Glorot weight initialization is applied by default
- Output layer: 10 nodes (for 10 classes) and softmax activation
network = models.Sequential()
network.add(layers.Dense(512, activation='relu', kernel_initializer='he_normal', input_shape=(28 * 28,)))
network.add(layers.Dense(512, activation='relu', kernel_initializer='he_normal'))
network.add(layers.Dense(10, activation='softmax'))
Model summary¶
- Lots of parameters (weights and biases) to learn!
- hidden layer 1 : (28 28 + 1) 512 = 401920
- hidden layer 2 : (512 + 1) * 512 = 262656
- output layer: (512 + 1) * 10 = 5130
network.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 512) 401920
dense_1 (Dense) (None, 512) 262656
dense_2 (Dense) (None, 10) 5130
=================================================================
Total params: 669,706
Trainable params: 669,706
Non-trainable params: 0
_________________________________________________________________
Choosing loss, optimizer, metrics¶
- Loss function
- Cross-entropy (log loss) for multi-class classification ($y_{true}$ is one-hot encoded)
- Use binary crossentropy for binary problems (single output node)
- Use sparse categorical crossentropy if $y_{true}$ is label-encoded (1,2,3,...)
- Optimizer
- Any of the optimizers we discussed before. RMSprop usually works well.
- Metrics
- To monitor performance during training and testing, e.g. accuracy
# Shorthand
network.compile(loss='categorical_crossentropy', optimizer='rmsprop', metrics=['accuracy'])
# Detailed
network.compile(loss=CategoricalCrossentropy(label_smoothing=0.01),
optimizer=RMSprop(learning_rate=0.001, momentum=0.0)
metrics=[Accuracy()])
Preprocessing: Normalization, Reshaping, Encoding¶
- Always normalize (standardize or min-max) the inputs. Mean should be close to 0.
- Avoid that some inputs overpower others
- Speed up convergence
- Gradients of activation functions $\frac{\partial a_{h}}{\partial z_{h}}$ are (near) 0 for large inputs
- If some gradients become much larger than others, SGD will start zig-zagging
- Reshape the data to fit the shape of the input layer, e.g. (n, 28*28) or (n, 28,28)
- Tensor with instances in first dimension, rest must match the input layer
- In multi-class classification, every class is an output node, so one-hot-encode the labels
- e.g. class '4' becomes [0,0,0,0,1,0,0,0,0,0]
X = X.astype('float32') / 255
X = X.reshape((60000, 28 * 28))
y = to_categorical(y)
Choosing training hyperparameters¶
- Number of epochs: enough to allow convergence
- Too much: model starts overfitting (or just wastes time)
- Batch size: small batches (e.g. 32, 64,... samples) often preferred
- 'Noisy' training data makes overfitting less likely
- Larger batches generalize less well ('generalization gap')
- Requires less memory (especially in GPUs)
- Large batches do speed up training, may converge in fewer epochs
- 'Noisy' training data makes overfitting less likely
- Batch size interacts with learning rate
- Instead of shrinking the learning rate you can increase batch size
history = network.fit(X_train, y_train, epochs=3, batch_size=32);
Epoch 1/3 1875/1875 [==============================] - 24s 13ms/step - loss: 0.4331 - accuracy: 0.8529 Epoch 2/3 1875/1875 [==============================] - 25s 13ms/step - loss: 0.4242 - accuracy: 0.8568 Epoch 3/3 1875/1875 [==============================] - 26s 14ms/step - loss: 0.4183 - accuracy: 0.8573
Predictions and evaluations¶
We can now call predict to generate predictions, and evaluate the trained model on the entire test set
network.predict(X_test)
test_loss, test_acc = network.evaluate(X_test, y_test)
[0.0240177 0.0001167 0.4472437 0.0056629 0.057807 0.000094 0.4632739 0.0000267 0.0017463 0.0000112]
313/313 [==============================] - 2s 7ms/step - loss: 0.3845 - accuracy: 0.8636 Test accuracy: 0.8636000156402588
Model selection¶
- How many epochs do we need for training?
- Train the neural net and track the loss after every iteration on a validation set
- You can add a callback to the fit version to get info on every epoch
- Best model after a few epochs, then starts overfitting
Early stopping¶
- Stop training when the validation loss (or validation accuracy) no longer improves
- Loss can be bumpy: use a moving average or wait for $k$ steps without improvement
earlystop = callbacks.EarlyStopping(monitor='val_loss', patience=3)
model.fit(x_train, y_train, epochs=25, batch_size=512, callbacks=[earlystop])
Regularization and memorization capacity¶
- The number of learnable parameters is called the model capacity
- A model with more parameters has a higher memorization capacity
- Too high capacity causes overfitting, too low causes underfitting
- In the extreme, the training set can be 'memorized' in the weights
- Smaller models are forced it to learn a compressed representation that generalizes better
- Find the sweet spot: e.g. start with few parameters, increase until overfitting stars.
- Example: 256 nodes in first layer, 32 nodes in second layer, similar performance
Information bottleneck¶
- If a layer is too narrow, it will lose information that can never be recovered by subsequent layers
- Information bottleneck theory defines a bound on the capacity of the network
- Imagine that you need to learn 10 outputs (e.g. classes) and your hidden layer has 2 nodes
- This is like trying to learn 10 hyperplanes from a 2-dimensional representation
- Example: bottleneck of 2 nodes, no overfitting, much higher training loss
Weight regularization (weight decay)¶
- As we did many times before, we can also add weight regularization to our loss function
- L1 regularization: leads to sparse networks with many weights that are 0
- L2 regularization: leads to many very small weights
network = models.Sequential()
network.add(layers.Dense(256, activation='relu', kernel_regularizer=regularizers.l2(0.001), input_shape=(28 * 28,)))
network.add(layers.Dense(128, activation='relu', kernel_regularizer=regularizers.l2(0.001)))
Dropout¶
- Every iteration, randomly set a number of activations $a_i$ to 0
- Dropout rate : fraction of the outputs that are zeroed-out (e.g. 0.1 - 0.5)
- Idea: break up accidental non-significant learned patterns
- At test time, nothing is dropped out, but the output values are scaled down by the dropout rate
- Balances out that more units are active than during training
Dropout layers¶
- Dropout is usually implemented as a special layer
network = models.Sequential()
network.add(layers.Dense(256, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dropout(0.5))
network.add(layers.Dense(32, activation='relu'))
network.add(layers.Dropout(0.5))
network.add(layers.Dense(10, activation='softmax'))
Batch Normalization¶
- We've seen that scaling the input is important, but what if layer activations become very large?
- Same problems, starting deeper in the network
- Batch normalization: normalize the activations of the previous layer within each batch
- Within a batch, set the mean activation close to 0 and the standard deviation close to 1
- Across badges, use exponential moving average of batch-wise mean and variance
- Allows deeper networks less prone to vanishing or exploding gradients
- Within a batch, set the mean activation close to 0 and the standard deviation close to 1
network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.BatchNormalization())
network.add(layers.Dropout(0.5))
network.add(layers.Dense(256, activation='relu'))
network.add(layers.BatchNormalization())
network.add(layers.Dropout(0.5))
network.add(layers.Dense(64, activation='relu'))
network.add(layers.BatchNormalization())
network.add(layers.Dropout(0.5))
network.add(layers.Dense(32, activation='relu'))
network.add(layers.BatchNormalization())
network.add(layers.Dropout(0.5))
Tuning multiple hyperparameters¶
- You can wrap Keras models as scikit-learn models and use any tuning technique
- Keras also has built-in RandomSearch (and HyperBand and BayesianOptimization - see later)
def make_model(hp):
m.add(Dense(units=hp.Int('units', min_value=32, max_value=512, step=32)))
m.compile(optimizer=Adam(hp.Choice('learning rate', [1e-2, 1e-3, 1e-4])))
return model
from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
clf = KerasClassifier(make_model)
grid = GridSearchCV(clf, param_grid=param_grid, cv=3)
from kerastuner.tuners import RandomSearch
tuner = keras.RandomSearch(build_model, max_trials=5)
Summary¶
- Neural architectures
- Training neural nets
- Forward pass: Tensor operations
- Backward pass: Backpropagation
- Neural network design:
- Activation functions
- Weight initialization
- Optimizers
- Neural networks in practice
- Model selection
- Early stopping
- Memorization capacity and information bottleneck
- L1/L2 regularization
- Dropout
- Batch normalization