Evaluation¶
- To know whether we can trust our method or system, we need to evaluate it.
- Model selection: choose between different models in a data-driven way.
- If you cannot measure it, you cannot improve it.
- Convince others that your work is meaningful
- Peers, leadership, clients, yourself(!)
- When possible, try to interpret what your model has learned
- The signal your model found may just be an artifact of your biased data
- See 'Why Should I Trust You?' by Marco Ribeiro et al.

Designing Machine Learning systems¶
- Just running your favourite algorithm is usually not a great way to start
- Consider the problem: How to measure success? Are there costs involved?
- Do you want to understand phenomena or do black box modelling?
- Analyze your model's mistakes. Don't just finetune endlessly.
- Build early prototypes. Should you collect more, or additional data?
- Should the task be reformulated?
- Overly complex machine learning systems are hard to maintain
- See 'Machine Learning: The High Interest Credit Card of Technical Debt'
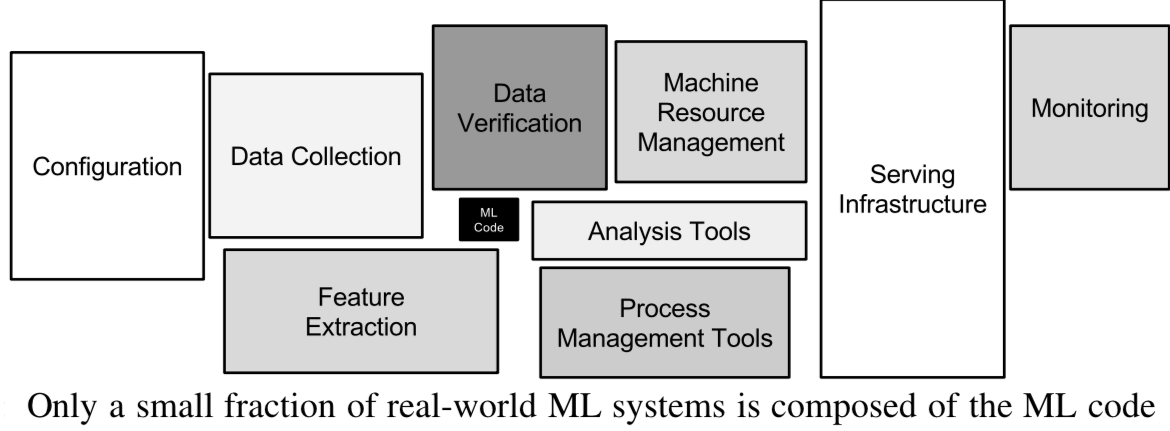
Real world evaluations¶
- Evaluate predictions, but also how outcomes improve because of them
- Beware of feedback loops: predictions can influence future input data
- Medical recommendations, spam filtering, trading algorithms,...
- Evaluate algorithms in the wild.
- A/B testing: split users in groups, test different models in parallel
- Bandit testing: gradually direct more users to the winning system
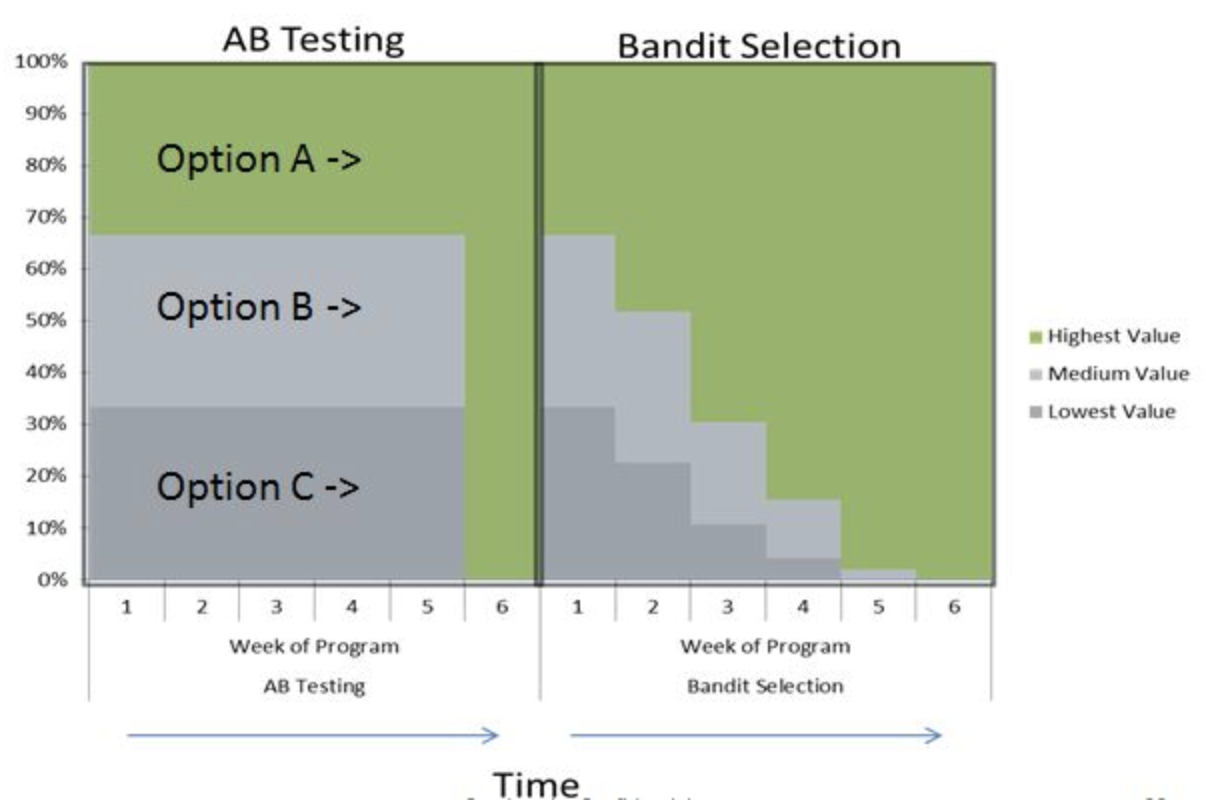
Performance estimation techniques¶
- Always evaluate models as if they are predicting future data
- We do not have access to future data, so we pretend that some data is hidden
- Simplest way: the holdout (simple train-test split)
- Randomly split data (and corresponding labels) into training and test set (e.g. 75%-25%)
- Train (fit) a model on the training data, score on the test data
K-fold Cross-validation¶
- Each random split can yield very different models (and scores)
- e.g. all easy (of hard) examples could end up in the test set
- Split data into k equal-sized parts, called folds
- Create k splits, each time using a different fold as the test set
- Compute k evaluation scores, aggregate afterwards (e.g. take the mean)
- Examine the score variance to see how sensitive (unstable) models are
- Large k gives better estimates (more training data), but is expensive
Can you explain this result?
kfold = KFold(n_splits=3)
cross_val_score(logistic_regression, iris.data, iris.target, cv=kfold)
Cross-validation scores KFold(n_splits=3): [0. 0. 0.]
Stratified K-Fold cross-validation¶
- If the data is unbalanced, some classes have only few samples
- Likely that some classes are not present in the test set
- Stratification: proportions between classes are conserved in each fold
- Order examples per class
- Separate the samples of each class in k sets (strata)
- Combine corresponding strata into folds
Leave-One-Out cross-validation¶
- k fold cross-validation with k equal to the number of samples
- Completely unbiased (in terms of data splits), but computationally expensive
- Actually generalizes less well towards unseen data
- The training sets are correlated (overlap heavily)
- Overfits on the data used for (the entire) evaluation
- A different sample of the data can yield different results
- Recommended only for small datasets
Shuffle-Split cross-validation¶
- Shuffles the data, samples (
train_size) points randomly as the training set - Can also use a smaller (
test_size), handy with very large datasets - Never use if the data is ordered (e.g. time series)
The Bootstrap¶
- Sample n (dataset size) data points, with replacement, as training set (the bootstrap)
- On average, bootstraps include 66% of all data points (some are duplicates)
- Use the unsampled (out-of-bootstrap) samples as the test set
- Repeat $k$ times to obtain $k$ scores
- Similar to Shuffle-Split with
train_size=0.66,test_size=0.34but without duplicates
Repeated cross-validation¶
- Cross-validation is still biased in that the initial split can be made in many ways
- Repeated, or n-times-k-fold cross-validation:
- Shuffle data randomly, do k-fold cross-validation
- Repeat n times, yields n times k scores
- Unbiased, very robust, but n times more expensive
Cross-validation with groups¶
- Sometimes the data contains inherent groups:
- Multiple samples from same patient, images from same person,...
- Data from the same person may end up in the training and test set
- We want to measure how well the model generalizes to other people
- Make sure that data from one person are in either the train or test set
- This is called grouping or blocking
- Leave-one-subject-out cross-validation: test set for each subject/group
Time series¶
When the data is ordered, random test sets are not a good idea
Test-then-train (prequential evaluation)¶
- Every new sample is evaluated only once, then added to the training set
- Can also be done in batches (of n samples at a time)
TimeSeriesSplit- In the kth split, the first k folds are the train set and the (k+1)th fold as the test set
- Often, a maximum training set size (or window) is used
- more robust against concept drift (change in data over time)
Choosing a performance estimation procedure¶
No strict rules, only guidelines:
- Always use stratification for classification (sklearn does this by default)
- Use holdout for very large datasets (e.g. >1.000.000 examples)
- Or when learners don't always converge (e.g. deep learning)
- Choose k depending on dataset size and resources
- Use leave-one-out for very small datasets (e.g. <100 examples)
- Use cross-validation otherwise
- Most popular (and theoretically sound): 10-fold CV
- Literature suggests 5x2-fold CV is better
- Use grouping or leave-one-subject-out for grouped data
- Use train-then-test for time series
Evaluation Metrics for Classification¶
Evaluation vs Optimization¶
Each algorithm optimizes a given objective function (on the training data)
- E.g. remember L2 loss in Ridge regression $$\mathcal{L}_{Ridge} = \sum_{n=1}^{N} (y_n-(\mathbf{w}\mathbf{x_n} + w_0))^2 + \alpha \sum_{i=0}^{p} w_i^2$$
The choice of function is limited by what can be efficiently optimized
- However, we evaluate the resulting model with a score that makes sense in the real world
- Percentage of correct predictions (on a test set)
- The actual cost of mistakes (e.g. in money, time, lives,...)
- We also tune the algorithm's hyperparameters to maximize that score
Binary classification¶
- We have a positive and a negative class
- 2 different kind of errors:
- False Positive (type I error): model predicts positive while true label is negative
- False Negative (type II error): model predicts negative while true label is positive
- They are not always equally important
- Which side do you want to err on for a medical test?

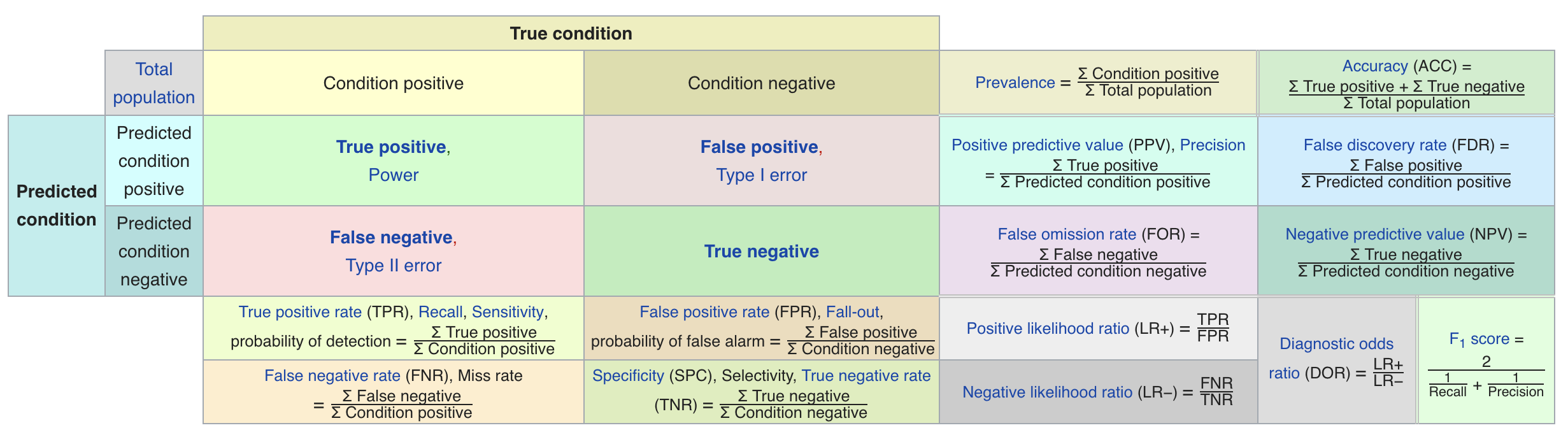
Confusion matrices¶
- We can represent all predictions (correct and incorrect) in a confusion matrix
- n by n array (n is the number of classes)
- Rows correspond to true classes, columns to predicted classes
- Count how often samples belonging to a class C are classified as C or any other class.
- For binary classification, we label these true negative (TN), true positive (TP), false negative (FN), false positive (FP)
| Predicted Neg | Predicted Pos | |
|---|---|---|
| Actual Neg | TN | FP |
| Actual Pos | FN | TP |
confusion_matrix(y_test, y_pred): [[48 5] [ 5 85]]
Predictive accuracy¶
- Accuracy can be computed based on the confusion matrix
- Not useful if the dataset is very imbalanced
- E.g. credit card fraud: is 99.99% accuracy good enough?
- 3 models: very different predictions, same accuracy:
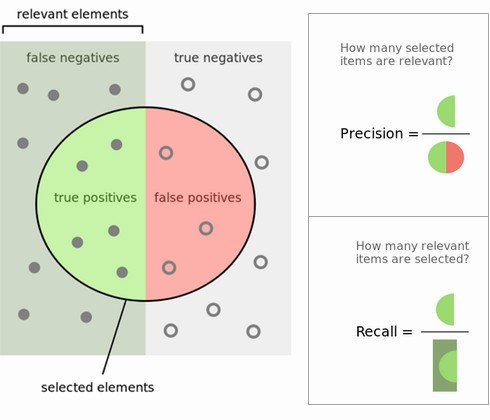
Precision¶
- Use when the goal is to limit FPs
- Clinical trails: you only want to test drugs that really work
- Search engines: you want to avoid bad search results
Recall¶
- Use when the goal is to limit FNs
- Cancer diagnosis: you don't want to miss a serious disease
- Search engines: You don't want to omit important hits
- Also know as sensitivity, hit rate, true positive rate (TPR)
Comparison
F1-score¶
- Trades off precision and recall:
Classification measure Zoo
Multi-class classification¶
Train models per class : one class viewed as positive, other(s) als negative, then average
micro-averaging: count total TP, FP, TN, FN (every sample equally important)
- micro-precision, micro-recall, micro-F1, accuracy are all the same $$\text{Precision:} \frac{\sum_{c=1}^C\text{TP}_c}{\sum_{c=1}^C\text{TP}_c + \sum_{c=1}^C\text{FP}_c} \xrightarrow{c=2} \frac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$
macro-averaging: average of scores $R(y_c,\hat{y_c})$ obtained on each class
- Preferable for imbalanced classes (if all classes are equally important)
- macro-averaged recall is also called balanced accuracy $$\frac{1}{C} \sum_{c=1}^C R(y_c,\hat{y_c})$$
- weighted averaging ($w_c$: ratio of examples of class $c$, aka support): $\sum_{c=1}^C w_c R(y_c,\hat{y_c})$
Other useful classification metrics¶
- Cohen's Kappa
- Measures 'agreement' between different models (aka inter-rater agreement)
- To evaluate a single model, compare it against a model that does random guessing
- Similar to accuracy, but taking into account the possibility of predicting the right class by chance
- Can be weighted: different misclassifications given different weights
- 1: perfect prediction, 0: random prediction, negative: worse than random
- With $p_0$ = accuracy, and $p_e$ = accuracy of random classifier: $$\kappa = \frac{p_o - p_e}{1 - p_e}$$
- Matthews correlation coefficient
- Corrects for imbalanced data, alternative for balanced accuracy or AUROC
- 1: perfect prediction, 0: random prediction, -1: inverse prediction $$MCC = \frac{tp \times tn - fp \times fn}{\sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}$$
Probabilistic evaluation¶
- Classifiers can often provide uncertainty estimates of predictions.
Remember that linear models actually return a numeric value.
- When $\hat{y}<0$, predict class -1, otherwise predict class +1 $$\hat{y} = w_0 * x_0 + w_1 * x_1 + ... + w_p * x_p + b $$
In practice, you are often interested in how certain a classifier is about each class prediction (e.g. cancer treatments).
- Most learning methods can return at least one measure of confidence in their predicions.
- Decision function: floating point value for each sample (higher: more confident)
- Probability: estimated probability for each class
The decision function¶
In the binary classification case, the return value of the decision function encodes how strongly the model believes a data point belongs to the “positive” class.
- Positive values indicate preference for the positive class.
- The range can be arbitrary, and can be affected by hyperparameters. Hard to interpret.
Predicting probabilities¶
Some models can also return a probability for each class with every prediction. These sum up to 1. We can visualize them again. Note that the gradient looks different now.
Threshold calibration¶
- By default, we threshold at 0 for
decision_functionand 0.5 forpredict_proba - Depending on the application, you may want to threshold differently
- Lower threshold yields fewer FN (better recall), more FP (worse precision), and vice-versa
interactive(children=(FloatSlider(value=2.220446049250313e-16, description='threshold', max=1.3, min=-1.2), Ou…
Precision-Recall curve¶
- The best trade-off between precision and recall depends on your application
- You can have arbitrary high recall, but you often want reasonable precision, too.
- Plotting precision against recall for all possible thresholds yields a precision-recall curve
- Change the treshold until you find a sweet spot in the precision-recall trade-off
- Often jagged at high thresholds, when there are few positive examples left
interactive(children=(FloatSlider(value=-0.9899999999999998, description='threshold', max=1.4, min=-3.19), Dro…
Model selection¶
- Some models can achieve trade-offs that others can't
- Your application may require very high recall (or very high precision)
- Choose the model that offers the best trade-off, given your application
- The area under the PR curve (AUPRC) gives the best overall model
Hyperparameter effects¶
Of course, hyperparameters affect predictions and hence also the shape of the curve
Receiver Operating Characteristics (ROC)¶
- Trade off true positive rate $\textit{TPR}= \frac{TP}{TP + FN}$ with false positive rate $\textit{FPR} = \frac{FP}{FP + TN}$
- Plotting TPR against FPR for all possible thresholds yields a Receiver Operating Characteristics curve
- Change the treshold until you find a sweet spot in the TPR-FPR trade-off
- Lower thresholds yield higher TPR (recall), higher FPR, and vice versa
interactive(children=(FloatSlider(value=-0.9899999999999998, description='threshold', max=1.4, min=-3.19), Dro…
Visualization¶
- Histograms show the amount of points with a certain decision value (for each class)
- $\textit{TPR}= \frac{\color{red}{TP}}{\color{red}{TP} + \color{magenta}{FN}}$ can be seen from the positive predictions (top histogram)
- $\textit{FPR} = \frac{\color{cyan}{FP}}{\color{cyan}{FP} + \color{blue}{TN}}$ can be seen from the negative predictions (bottom histogram)
interactive(children=(FloatSlider(value=0.0, description='threshold', max=2.0, min=-2.0), Output()), _dom_clas…
Model selection¶
- Again, some models can achieve trade-offs that others can't
- Your application may require minizing FPR (low FP), or maximizing TPR (low FN)
- The area under the ROC curve (AUROC or AUC) gives the best overall model
- Frequently used for evaluating models on imbalanced data
- Random guessing (TPR=FPR) or predicting majority class (TPR=FPR=1): 0.5 AUC
Multi-class AUROC (or AUPRC)¶
- We again need to choose between micro- or macro averaging TPR and FPR.
- Micro-average if every sample is equally important (irrespective of class)
- Macro-average if every class is equally important, especially for imbalanced data
Model calibration¶
- For some models, the predicted uncertainty does not reflect the actual uncertainty
- If a model is 90% sure that samples are positive, is it also 90% accurate on these?
- A model is called calibrated if the reported uncertainty actually matches how correct it is
- Overfitted models also tend to be over-confident
- LogisticRegression models are well calibrated since they learn probabilities
- SVMs are not well calibrated. Biased towards points close to the decision boundary.
Brier score¶
- You may want to select models based on how accurate the class confidences are.
- The Brier score loss: squared loss between predicted probability $\hat{p}$ and actual outcome $y$
- Lower is better $$\mathcal{L}_{Brier} = \frac{1}{n}\sum_{i=1}^n (\hat{p}_i - y_i)^2$$
Logistic Regression Brier score loss: 0.0322 SVM Brier score loss: 0.0795
Model calibration techniques¶
- We can post-process trained models to make them more calibrated.
- Fit a regression model (a calibrator) to map the model's outcomes $f(x)$ to a calibrated probability in [0,1]
- $f(x)$ returns the decision values or probability estimates
- $f_{calib}$ is fitted on the training data to map these to the correct outcome
- Often an internal cross-validation with few folds is used
- Multi-class models require one calibrator per class
Platt Scaling¶
- Calibrator is a logistic (sigmoid) function:
- Learn the weight $w_1$ and bias $w_0$ from data $$f_{platt}=\frac{1}{1+\exp(−w_1 f(x)− w_0)}$$
Isotonic regression¶
- Maps input $x_i$ to an output $\hat{y}_i$ so that $\hat{y}_i$ increases monotonically with $x_i$ and minimizes loss $\sum_i^n (y_i-\hat{y}_i)$
- Predictions are made by interpolating the predicted $\hat{y}_i$
- Fit to minimize the loss between the uncalibrated predictions $f(x)$ and the actual labels
- Corrects any monotonic distortion, but tends to overfit on small samples
Cost-sensitive classification (dealing with imbalance)¶
- In the real worlds, different kinds of misclassification can have different costs
- Misclassifying certain classes can be more costly than others
- Misclassifying certain samples can be more costly than others
- Cost-sensitive resampling: resample (or reweight) the data to represent real-world expectations
- oversample minority classes (or undersample majority) to 'correct' imbalance
- increase weight of misclassified samples (e.g. in boosting)
- decrease weight of misclassified (noisy) samples (e.g. in model compression)
Class weighting¶
- If some classes are more important than others, we can give them more weight
- E.g. for imbalanced data, we can give more weight to minority classes
- Most classification models can include it in their loss function and optimize for it
- E.g. Logistic regression: add a class weight $w_c$ in the log loss function $$\mathcal{L_{log}}(\mathbf{w}) = - \sum_{c=1}^{C} \color{red}{w_c} \sum_{n=1}^{N} p_{n,c} log(q_{n,c}) $$
Instance weighting¶
- If some training instances are important to get right, we can give them more weight
- E.g. when some examples are from groups underrepresented in the data
- These are passed during training (fit), and included in the loss function
- E.g. Logistic regression: add a instance weight $w_n$ in the log loss function $$\mathcal{L_{log}}(\mathbf{w}) = - \sum_{c=1}^{C} \sum_{n=1}^{N} \color{red}{w_n} p_{n,c} log(q_{n,c}) $$
Cost-sensitive algorithms¶
- Cost-sensitive algorithms
- If misclassification cost of some classes is higher, we can give them higher weights
- Some support cost matrix $C$: costs $c_{i,j}$ for every possible type of error
- Cost-sensitive ensembles: convert cost-insensitive classifiers into cost-sensitive ones
- MetaCost: Build a model (ensemble) to learn the class probabilities $P(j|x)$
- Relabel training data to minimize expected cost: $\underset{i}{\operatorname{argmin}} \sum_j P_j(x) c_{i,j}$
- Accuracy may decrease but cost decreases as well.
- AdaCost: Boosting with reweighting instances to reduce costs
- MetaCost: Build a model (ensemble) to learn the class probabilities $P(j|x)$
Tuning the decision threshold¶
- If every FP or FN has a certain cost, we can compute the total cost for a given model: $$\text{total cost} = \text{FPR} * cost_{FP} * ratio_{pos} + (1-\text{TPR}) * cost_{FN} * (1-ratio_{pos})$$
- This yields different isometrics (lines of equal cost) in ROC space
- Optimal threshold is the point on the ROC curve where cost is minimal (line search)
interactive(children=(FloatSlider(value=5.0, description='cost_FN', max=10.0, min=1.0, step=1.0), FloatSlider(…
Regression metrics¶
Most commonly used are
- mean squared error: $\frac{\sum_{i}(y_{pred_i}-y_{actual_i})^2}{n}$
- root mean squared error (RMSE) often used as well
- mean absolute error: $\frac{\sum_{i}|y_{pred_i}-y_{actual_i}|}{n}$
- Less sensitive to outliers and large errors

R squared¶
- $R^2 = 1 - \frac{\color{blue}{\sum_{i}(y_{pred_i}-y_{actual_i})^2}}{\color{red}{\sum_{i}(y_{mean}-y_{actual_i})^2}}$
- Ratio of variation explained by the model / total variation
- Between 0 and 1, but negative if the model is worse than just predicting the mean
- Easier to interpret (higher is better).
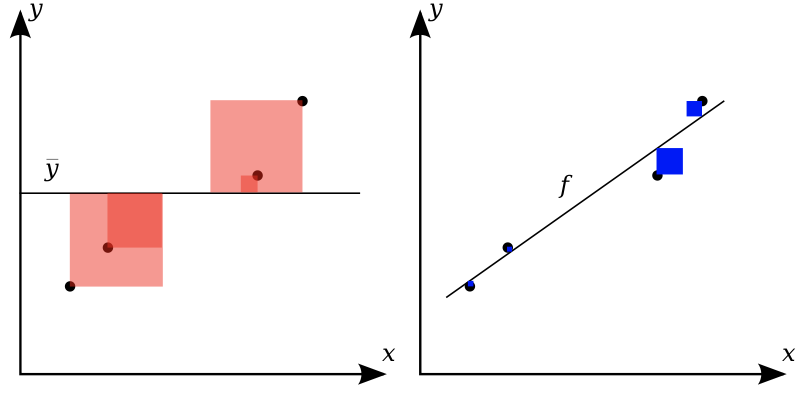
Visualizing regression errors¶
- Prediction plot (left): predicted vs actual target values
- Residual plot (right): residuals vs actual target values
- Over- and underpredictions can be given different costs
Bias-Variance decomposition¶
- Evaluate the same algorithm multiple times on different random samples of the data
- Two types of errors can be observed:
- Bias error: systematic error, independent of the training sample
- These points are predicted (equally) wrong every time
- Variance error: error due to variability of the model w.r.t. the training sample
- These points are sometimes predicted accurately, sometimes inaccurately
- Bias error: systematic error, independent of the training sample
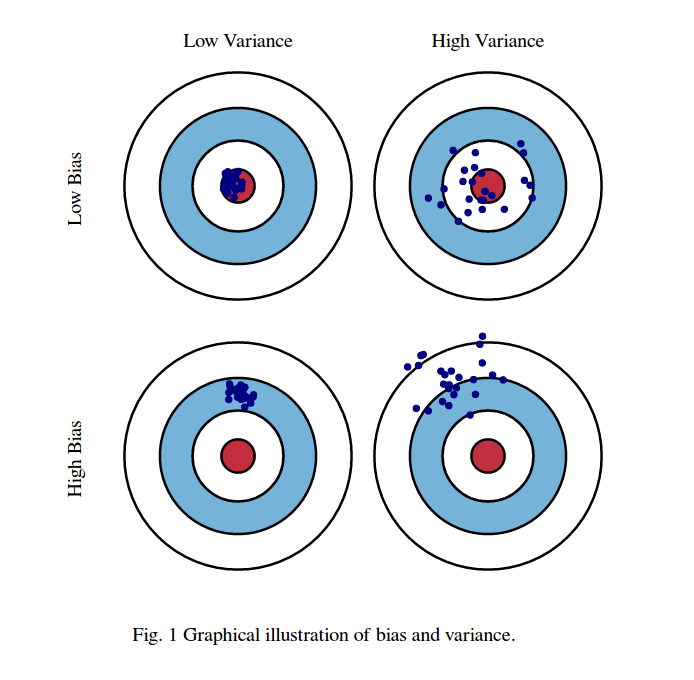
Computing bias and variance error¶
- Take 100 or more bootstraps (or shuffle-splits)
- Regression: for each data point x:
- $bias(x)^2 = (x_{true} - mean(x_{predicted}))^2$
- $variance(x) = var(x_{predicted})$
- Classification: for each data point x:
- $bias(x)$ = misclassification ratio
- $variance(x) = (1 - (P(class_1)^2 + P(class_2)^2))/2$
- $P(class_i)$ is ratio of class $i$ predictions
- Total bias: $\sum_{x} bias(x)^2 * w_x$ $w_x$: the percentage of times $x$ occurs in the test sets
- Total variance: $\sum_{x} variance(x) * w_x$
Bias and variance, underfitting and overfitting¶
- High variance means that you are likely overfitting
- Use more regularization or use a simpler model
- High bias means that you are likely underfitting
- Do less regularization or use a more flexible/complex model
- Ensembling techniques (see later) reduce bias or variance directly
- Bagging (e.g. RandomForests) reduces variance, Boosting reduces bias
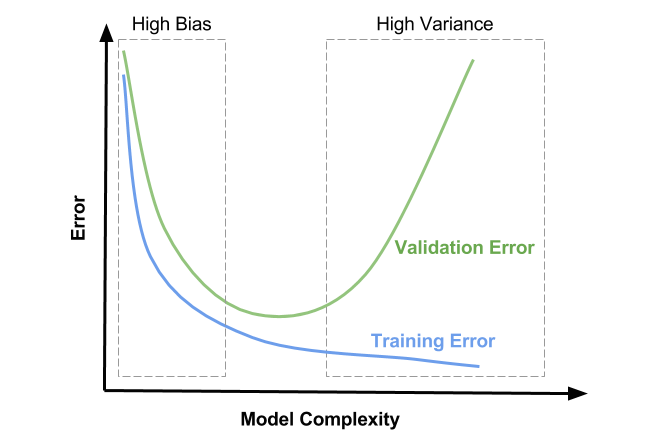
Understanding under- and overfitting¶
- Regularization reduces variance error (increases stability of predictions)
- But too much increases bias error (inability to learn 'harder' points)
- High regularization (left side): Underfitting, high bias error, low variance error
- High training error and high test error
- Low regularization (right side): Overfitting, low bias error, high variance error
- Low training error and higher test error
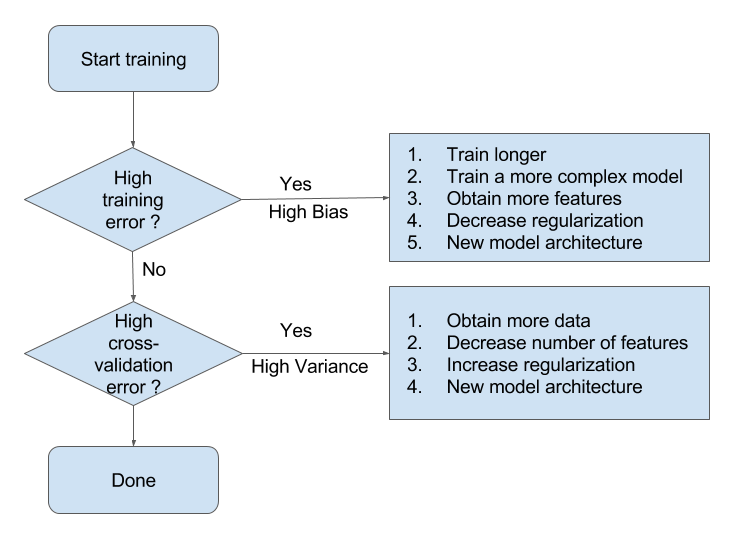
Summary Flowchart (by Andrew Ng)
Hyperparameter tuning¶
- There exists a huge range of techniques to tune hyperparameters. The simplest:
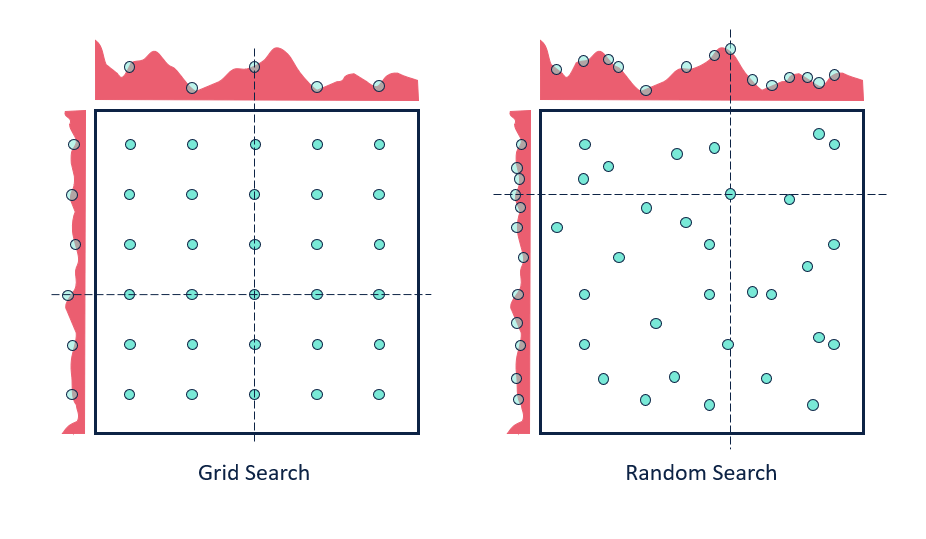
- Grid search: Choose a range of values for every hyperparameter, try every combination
- Doesn't scale to many hyperparameters (combinatorial explosion)
- Random search: Choose random values for all hyperparameters, iterate $n$ times
- Better, especially when some hyperparameters are less important
- Grid search: Choose a range of values for every hyperparameter, try every combination
- Many more advanced techniques exist, see lecture on Automated Machine Learning
- First, split the data in training and test sets (outer split)
- Split up the training data again (inner cross-validation)
- Generate hyperparameter configurations (e.g. random/grid search)
- Evaluate all configurations on all inner splits, select the best one (on average)
- Retrain best configurations on full training set, evaluate on held-out test data
Nested cross-validation¶
- Simplest approach: single outer split and single inner split (shown below)
- Risk of over-tuning hyperparameters on specific train-test split
- Only recommended for very large datasets
- Nested cross-validation:
- Outer loop: split full dataset in $k_1$ training and test splits
- Inner loop: split training data into $k_2$ train and validation sets
- This yields $k_1$ scores for $k_1$ possibly different hyperparameter settings
- Average score is the expected performance of the tuned model
- To use the model in practice, retune on the entire dataset
hps = {'C': expon(scale=100), 'gamma': expon(scale=.1)}
scores = cross_val_score(RandomizedSearchCV(SVC(), hps, cv=3), X, y, cv=5)
Summary¶
- Split the data into training and test sets according to the application
- Holdout only for large datasets, cross-validation for smaller ones
- For classification, always use stratification
- Grouped or ordered data requires special splitting
- Choose a metric that fits your application
- E.g. precision to avoid false positives, recall to avoid false negatives
- Calibrate the decision threshold to fit your application
- ROC curves or Precision-Recall curves can help to find a good tradeoff
- If possible, include the actual or relative costs of misclassifications
- Class weighting, instance weighting, ROC isometrics can help
- Be careful with imbalanced or unrepresentative datasets
- When using the predicted probabilities in applications, calibrate the models
- Always tune the most important hyperparameters
- Manual tuning: Use insight and train-test scores for guidance
- Hyperparameter optimization: be careful not to over-tune