Notation and Definitions¶
- A scalar is a simple numeric value, denoted by an italic letter: $x=3.24$
- A vector is a 1D ordered array of n scalars, denoted by a bold letter: $\mathbf{x}=[3.24, 1.2]$
- $x_i$ denotes the $i$th element of a vector, thus $x_0 = 3.24$.
- Note: some other courses use $x^{(i)}$ notation
- $x_i$ denotes the $i$th element of a vector, thus $x_0 = 3.24$.
- A set is an unordered collection of unique elements, denote by caligraphic capital: $\mathcal{S}=\{3.24, 1.2\}$
- A matrix is a 2D array of scalars, denoted by bold capital: $\mathbf{X}=\begin{bmatrix}
3.24 & 1.2 \\
2.24 & 0.2
\end{bmatrix}$
- $\textbf{X}_{i}$ denotes the $i$th row of the matrix
- $\textbf{X}_{:,j}$ denotes the $j$th column
- $\textbf{X}_{i,j}$ denotes the element in the $i$th row, $j$th column, thus $\mathbf{X}_{1,0} = 2.24$
- $\mathbf{X}^{n \times p}$, an $n \times p$ matrix, can represent $n$ data points in a $p$-dimensional space
- Every row is a vector that can represent a point in an p-dimensional space, given a basis.
- The standard basis for a Euclidean space is the set of unit vectors
- E.g. if $\mathbf{X}=\begin{bmatrix} 3.24 & 1.2 \\ 2.24 & 0.2 \\ 3.0 & 0.6 \end{bmatrix}$
- A tensor is an k-dimensional array of data, denoted by an italic capital: $T$
- k is also called the order, degree, or rank
- $T_{i,j,k,...}$ denotes the element or sub-tensor in the corresponding position
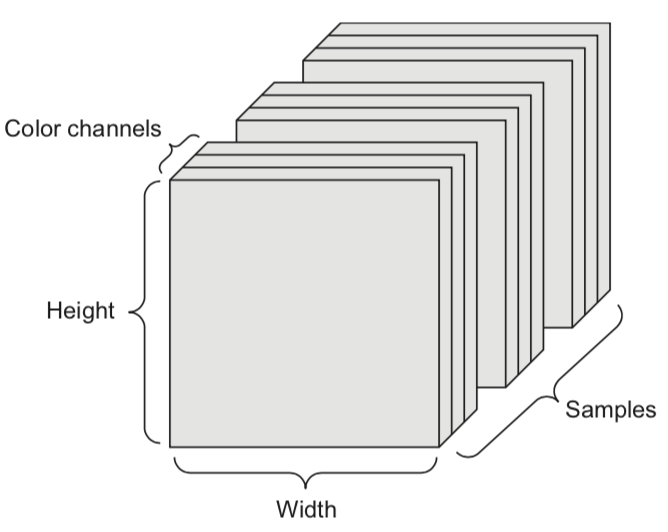
- A set of color images can be represented by:
- a 4D tensor (sample x height x width x color channel)
- a 2D tensor (sample x flattened vector of pixel values)
Basic operations¶
- Sums and products are denoted by capital Sigma and capital Pi:
$$\sum_{i=0}^{p} = x_0 + x_1 + ... + x_p \quad \prod_{i=0}^{p} = x_0 \cdot x_1 \cdot ... \cdot x_p$$
- Operations on vectors are element-wise: e.g. $\mathbf{x}+\mathbf{z} = [x_0+z_0,x_1+z_1, ... , x_p+z_p]$
- Dot product $\mathbf{w}\mathbf{x} = \mathbf{w} \cdot \mathbf{x} = \mathbf{w}^{T} \mathbf{x} = \sum_{i=0}^{p} w_i \cdot x_i = w_0 \cdot x_0 + w_1 \cdot x_1 + ... + w_p \cdot x_p$
- Matrix product $\mathbf{W}\mathbf{x} = \begin{bmatrix} \mathbf{w_0} \cdot \mathbf{x} \\ ... \\ \mathbf{w_p} \cdot \mathbf{x} \end{bmatrix}$
- A function $f(x) = y$ relates an input element $x$ to an output $y$
- It has a local minimum at $x=c$ if $f(x) \geq f(c)$ in interval $(c-\epsilon, c+\epsilon)$
- It has a global minimum at $x=c$ if $f(x) \geq f(c)$ for any value for $x$
- A vector function consumes an input and produces a vector: $\mathbf{f}(\mathbf{x}) = \mathbf{y}$
- $\underset{x\in X}{\operatorname{max}}f(x)$ returns the largest value f(x) for any x
- $\underset{x\in X}{\operatorname{argmax}}f(x)$ returns the element x that maximizes f(x)
Gradients¶
- A derivative $f'$ of a function $f$ describes how fast $f$ grows or decreases
- The process of finding a derivative is called differentiation
- Derivatives for basic functions are known
- For non-basic functions we use the chain rule: $F(x) = f(g(x)) \rightarrow F'(x)=f'(g(x))g'(x)$
- A function is differentiable if it has a derivative in any point of it's domain
- It's continuously differentiable if $f'$ is a continuous function
- We say $f$ is smooth if it is infinitely differentiable, i.e., $f', f'', f''', ...$ all exist
- A gradient $\nabla f$ is the derivative of a function in multiple dimensions
- It is a vector of partial derivatives: $\nabla f = \left[ \frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial x_1},... \right]$
- E.g. $f=2x_0+3x_1^{2}-\sin(x_2) \rightarrow \nabla f= [2, 6x_1, -cos(x_2)]$
- Example: $f = -(x_0^2+x_1^2)$
- $\nabla f = \left[\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1}\right] = \left[-2x_0,-2x_1\right]$
- Evaluated at point (-4,1): $\nabla f(-4,1) = [8,-2]$
- These are the slopes at point (-4,1) in the direction of $x_0$ and $x_1$ respectively
interactive(children=(IntSlider(value=120, description='rotation', max=240, step=10), Output()), _dom_classes=…
Distributions and Probabilities¶
- The normal (Gaussian) distribution with mean $\mu$ and standard deviation $\sigma$ is noted as $N(\mu,\sigma)$
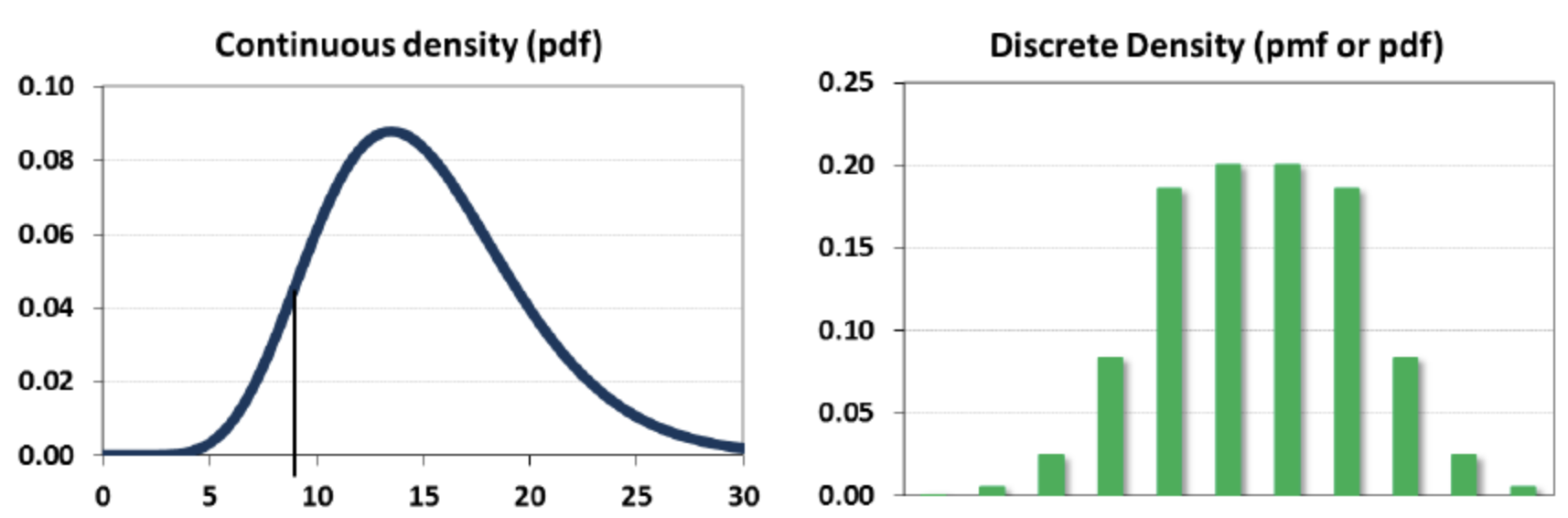
- A random variable $X$ can be continuous or discrete
- A probability distribution $f_X$ of a continuous variable $X$: probability density function (pdf)
- The expectation is given by $\mathbb{E}[X] = \int x f_{X}(x) dx$
- A probability distribution of a discrete variable: probability mass function (pmf)
- The expectation (or mean) $\mu_X = \mathbb{E}[X] = \sum_{i=1}^k[x_i \cdot Pr(X=x_i)]$
Linear models¶
Linear models make a prediction using a linear function of the input features $X$
$$f_{\mathbf{w}}(\mathbf{x}) = \sum_{i=1}^{p} w_i \cdot x_i + w_{0}$$
Learn $w$ from $X$, given a loss function $\mathcal{L}$:
$$\underset{\mathbf{w}}{\operatorname{argmin}} \mathcal{L}(f_\mathbf{w}(X))$$
- Many algorithms with different $\mathcal{L}$: Least squares, Ridge, Lasso, Logistic Regression, Linear SVMs,...
- Can be very powerful (and fast), especially for large datasets with many features.
- Can be generalized to learn non-linear patterns: Generalized Linear Models
- Features can be augmentented with polynomials of the original features
- Features can be transformed according to a distribution (Poisson, Tweedie, Gamma,...)
- Some linear models (e.g. SVMs) can be kernelized to learn non-linear functions
Linear models for regression¶
- Prediction formula for input features x:
- $w_1$ ... $w_p$ usually called weights or coefficients , $w_0$ the bias or intercept
- Assumes that errors are $N(0,\sigma)$
$$\hat{y} = \mathbf{w}\mathbf{x} + w_0 = \sum_{i=1}^{p} w_i \cdot x_i + w_0 = w_1 \cdot x_1 + w_2 \cdot x_2 + ... + w_p \cdot x_p + w_0 $$
w_1: 0.393906 w_0: -0.031804
Linear Regression (aka Ordinary Least Squares)¶
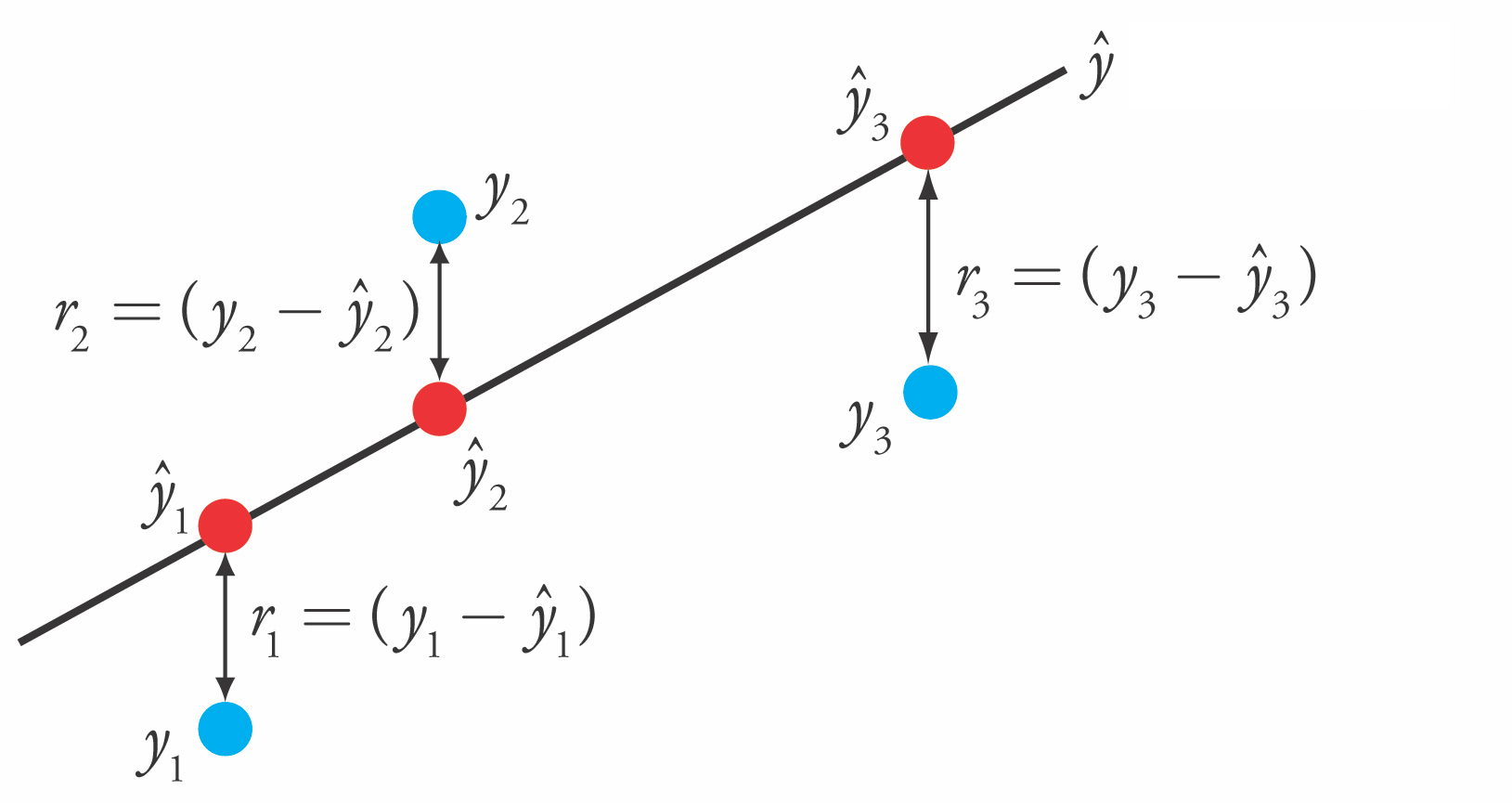
- Loss function is the sum of squared errors (SSE) (or residuals) between predictions $\hat{y}_i$ (red) and the true regression targets $y_i$ (blue) on the training set.
$$\mathcal{L}_{SSE} = \sum_{n=1}^{N} (y_n-\hat{y}_n)^2 = \sum_{n=1}^{N} (y_n-(\mathbf{w}\mathbf{x_n} + w_0))^2$$
Solving ordinary least squares¶
Convex optimization problem with unique closed-form solution:
$$w^{*} = (X^{T}X)^{-1} X^T Y$$
- Add a column of 1's to the front of X to get $w_0$
- Slow. Time complexity is quadratic in number of features: $\mathcal{O}(p^2n)$
- X has $n$ rows, $p$ features, hence $X^{T}X$ has dimensionality $p \cdot p$
- Only works if $n>p$
Gradient Descent
- Faster for large and/or high-dimensional datasets
- When $X^{T}X$ cannot be computed or takes too long ($p$ or $n$ is too large)
- When you want more control over the learning process
Very easily overfits.
- coefficients $w$ become very large (steep incline/decline)
- small change in the input x results in a very different output y
- No hyperparameters that control model complexity
Gradient Descent¶
Start with an initial, random set of weights: $\mathbf{w}^0$
Given a differentiable loss function $\mathcal{L}$ (e.g. $\mathcal{L}_{SSE}$), compute $\nabla \mathcal{L}$
For least squares: $\frac{\partial \mathcal{L}_{SSE}}{\partial w_i}(\mathbf{w}) = -2\sum_{n=1}^{N} (y_n-\hat{y}_n) x_{n,i}$
- If feature $X_{:,i}$ is associated with big errors, the gradient wrt $w_i$ will be large
Update all weights slightly (by step size or learning rate $\eta$) in 'downhill' direction.
Basic update rule (step s):
$$\mathbf{w}^{s+1} = \mathbf{w}^s-\eta\nabla \mathcal{L}(\mathbf{w}^s)$$
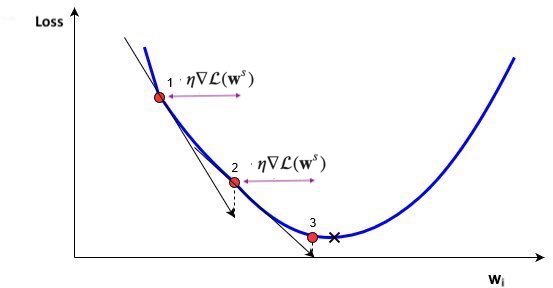
- Important hyperparameters
- Learning rate
- Too small: slow convergence. Too large: possible divergence
- Maximum number of iterations
- Too small: no convergence. Too large: wastes resources
- Learning rate decay with decay rate $k$
- E.g. exponential ($\eta^{s+1} = \eta^{0} e^{-ks}$), inverse-time ($\eta^{s+1} = \frac{\eta^{s}}{1+ks}$),...
- Many more advanced ways to control learning rate (see later)
- Adaptive techniques: depend on how much loss improved in previous step
- Learning rate
interactive(children=(FloatSlider(value=0.2, description='learn_rate', max=0.4, min=0.01, step=0.01), Checkbox…
Effect of learning rate
interactive(children=(IntSlider(value=50, description='iterations', min=1), FloatSlider(value=0.025, descripti…
Effect of learning rate decay
interactive(children=(IntSlider(value=50, description='iterations', min=1), Dropdown(description='optimizer1',…
In two dimensions:
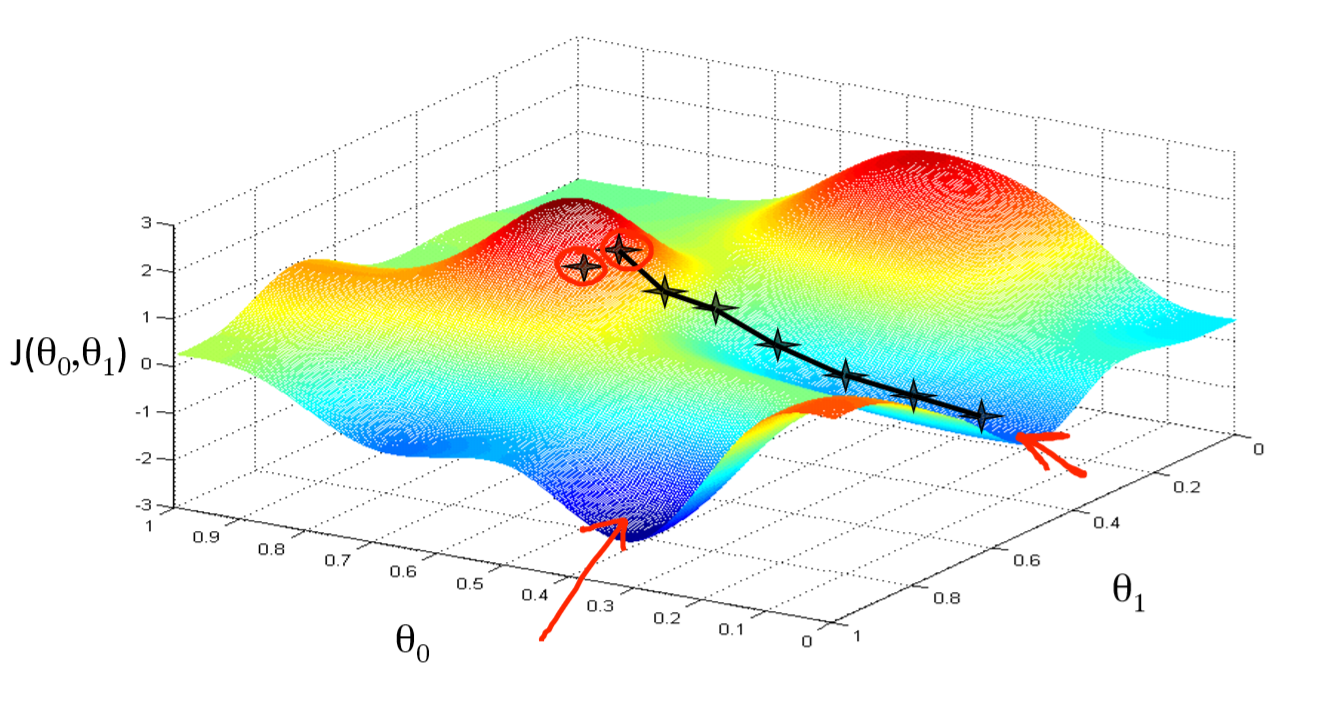
- You can get stuck in local minima (if the loss is not fully convex)
- If you have many model parameters, this is less likely
- You always find a way down in some direction
- Models with many parameters typically find good local minima
- Intuition: walking downhill using only the slope you "feel" nearby

(Image by A. Karpathy)
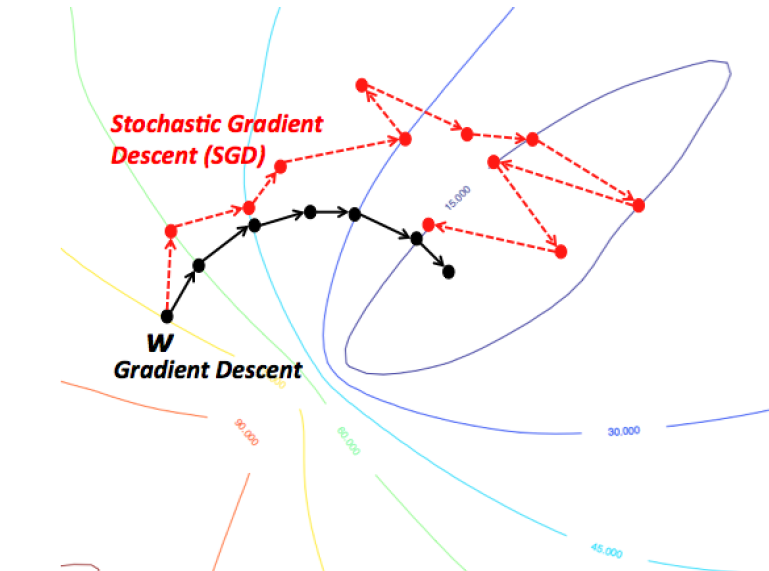
Stochastic Gradient Descent (SGD)¶
- Compute gradients not on the entire dataset, but on a single data point $i$ at a time
- Gradient descent: $\mathbf{w}^{s+1} = \mathbf{w}^s-\eta\nabla \mathcal{L}(\mathbf{w}^s) = \mathbf{w}^s-\frac{\eta}{n} \sum_{i=1}^{n} \nabla \mathcal{L_i}(\mathbf{w}^s)$
- Stochastic Gradient Descent: $\mathbf{w}^{s+1} = \mathbf{w}^s-\eta\nabla \mathcal{L_i}(\mathbf{w}^s)$
- Many smoother variants, e.g.
- Minibatch SGD: compute gradient on batches of data: $\mathbf{w}^{s+1} = \mathbf{w}^s-\frac{\eta}{B} \sum_{i=1}^{B} \nabla \mathcal{L_i}(\mathbf{w}^s)$
- Stochastic Average Gradient Descent (SAG, SAGA). With $i_s \in [1,n]$ randomly chosen per iteration:
- Incremental gradient: $\mathbf{w}^{s+1} = \mathbf{w}^s-\frac{\eta}{n} \sum_{i=1}^{n} v_i^s$ with $v_i^s = \begin{cases}\nabla \mathcal{L_i}(\mathbf{w}^s) & i = i_s \\ v_i^{s-1} & \text{otherwise} \end{cases}$
In practice¶
- Linear regression can be found in
sklearn.linear_model. We'll evaluate it on the Boston Housing dataset.LinearRegressionuses closed form solution,SGDRegressorwithloss='squared_loss'uses Stochastic Gradient Descent- Large coefficients signal overfitting
- Test score is much lower than training score
from sklearn.linear_model import LinearRegression
lr = LinearRegression().fit(X_train, y_train)
Weights (coefficients): [ -412.711 -52.243 -131.899 -12.004 -15.511 28.716 54.704
-49.535 26.582 37.062 -11.828 -18.058 -19.525 12.203
2980.781 1500.843 114.187 -16.97 40.961 -24.264 57.616
1278.121 -2239.869 222.825 -2.182 42.996 -13.398 -19.389
-2.575 -81.013 9.66 4.914 -0.812 -7.647 33.784
-11.446 68.508 -17.375 42.813 1.14 ]
Bias (intercept): 30.93456367364179
Training set score (R^2): 0.95 Test set score (R^2): 0.61
Ridge regression¶
- Adds a penalty term to the least squares loss function:
$$\mathcal{L}_{Ridge} = \sum_{n=1}^{N} (y_n-(\mathbf{w}\mathbf{x_n} + w_0))^2 + \alpha \sum_{i=1}^{p} w_i^2$$
- Model is penalized if it uses large coefficients ($w$)
- Each feature should have as little effect on the outcome as possible
- We don't want to penalize $w_0$, so we leave it out
- Regularization: explicitly restrict a model to avoid overfitting.
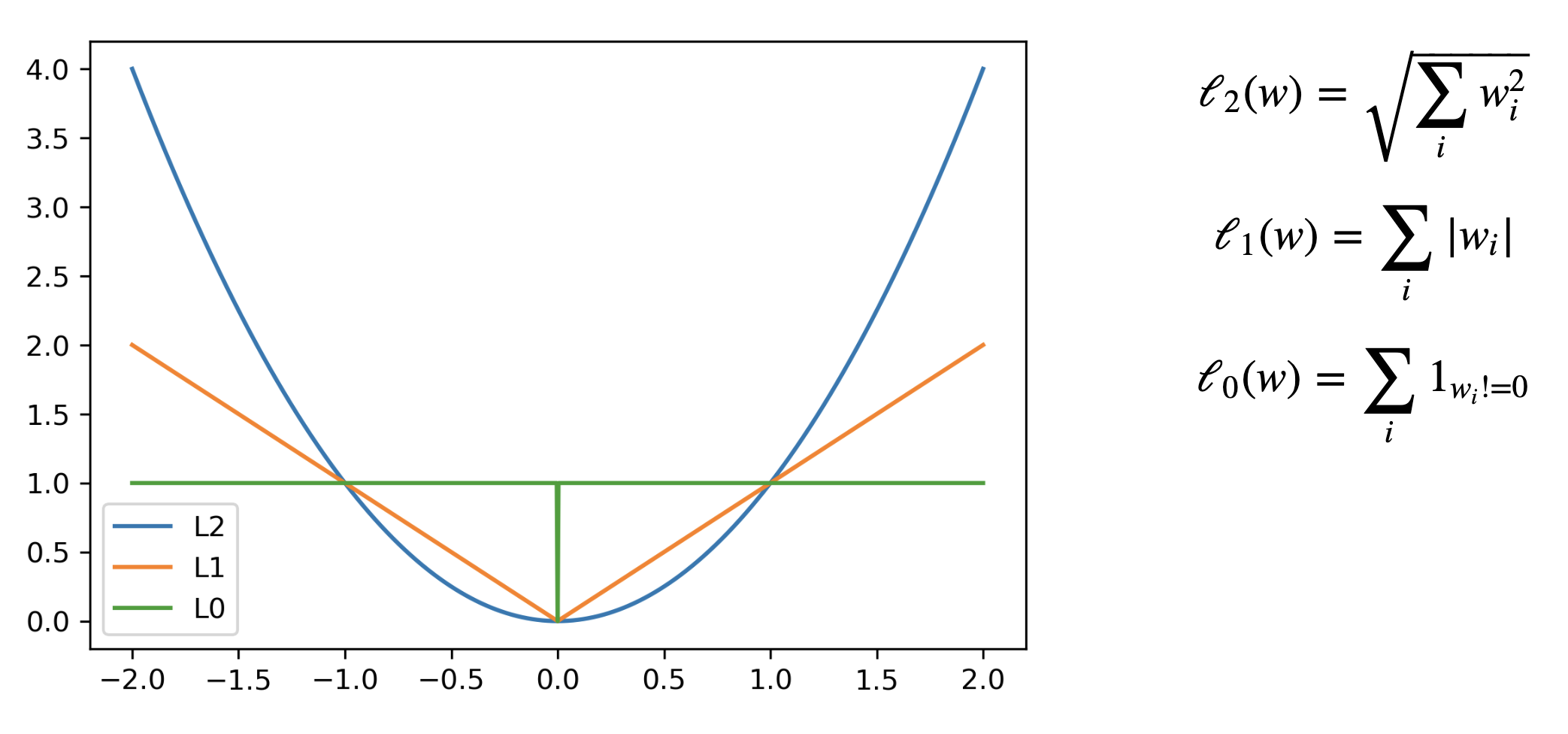
- Called L2 regularization because it uses the L2 norm: $\sum w_i^2$
- The strength of the regularization can be controlled with the $\alpha$ hyperparameter.
- Increasing $\alpha$ causes more regularization (or shrinkage). Default is 1.0.
- Still convex. Can be optimized in different ways:
- Closed form solution (a.k.a. Cholesky): $w^{*} = (X^{T}X + \alpha I)^{-1} X^T Y$
- Gradient descent and variants, e.g. Stochastic Average Gradient (SAG,SAGA)
- Conjugate gradient (CG): each new gradient is influenced by previous ones
- Use Cholesky for smaller datasets, Gradient descent for larger ones
In practice¶
from sklearn.linear_model import Ridge
lr = Ridge().fit(X_train, y_train)
Weights (coefficients): [-1.414 -1.557 -1.465 -0.127 -0.079 8.332 0.255 -4.941 3.899 -1.059 -1.584 1.051 -4.012 0.334 0.004 -0.849 0.745 -1.431 -1.63 -1.405 -0.045 -1.746 -1.467 -1.332 -1.692 -0.506 2.622 -2.092 0.195 -0.275 5.113 -1.671 -0.098 0.634 -0.61 0.04 -1.277 -2.913 3.395 0.792] Bias (intercept): 21.39052595861006 Training set score: 0.89 Test set score: 0.75
Test set score is higher and training set score lower: less overfitting!
- We can plot the weight values for differents levels of regularization to explore the effect of $\alpha$.
- Increasing regularization decreases the values of the coefficients, but never to 0.
interactive(children=(FloatSlider(value=5.0, description='alpha', max=10.0, step=0.05), Output()), _dom_classe…
- When we plot the train and test scores for every $\alpha$ value, we see a sweet spot around $\alpha=0.2$
- Models with smaller $\alpha$ are overfitting
- Models with larger $\alpha$ are underfitting
Other ways to reduce overfitting¶
- Add more training data: with enough training data, regularization becomes less important
- Ridge and ordinary least squares will have the same performance
- Use fewer features: remove unimportant ones or find a low-dimensional embedding (e.g. PCA)
- Fewer coefficients to learn, reduces the flexibility of the model
- Scaling the data typically helps (and changes the optimal $\alpha$ value)
Lasso (Least Absolute Shrinkage and Selection Operator)¶
- Adds a different penalty term to the least squares sum:
$$\mathcal{L}_{Lasso} = \sum_{n=1}^{N} (y_n-(\mathbf{w}\mathbf{x_n} + w_0))^2 + \alpha \sum_{i=1}^{p} |w_i|$$
- Called L1 regularization because it uses the L1 norm
- Will cause many weights to be exactly 0
- Same parameter $\alpha$ to control the strength of regularization.
- Will again have a 'sweet spot' depending on the data
- No closed-form solution
- Convex, but no longer strictly convex, and not differentiable
- Weights can be optimized using coordinate descent
Analyze what happens to the weights:
- L1 prefers coefficients to be exactly zero (sparse models)
- Some features are ignored entirely: automatic feature selection
- How can we explain this?
interactive(children=(FloatSlider(value=0.25, description='alpha', max=0.5, step=0.005), Output()), _dom_class…
Coordinate descent¶
- Alternative for gradient descent, supports non-differentiable convex loss functions (e.g. $\mathcal{L}_{Lasso}$)
- In every iteration, optimize a single coordinate $w_i$ (find minimum in direction of $x_i$)
- Continue with another coordinate, using a selection rule (e.g. round robin)
- Faster iterations. No need to choose a step size (learning rate).
- May converge more slowly. Can't be parallellized.
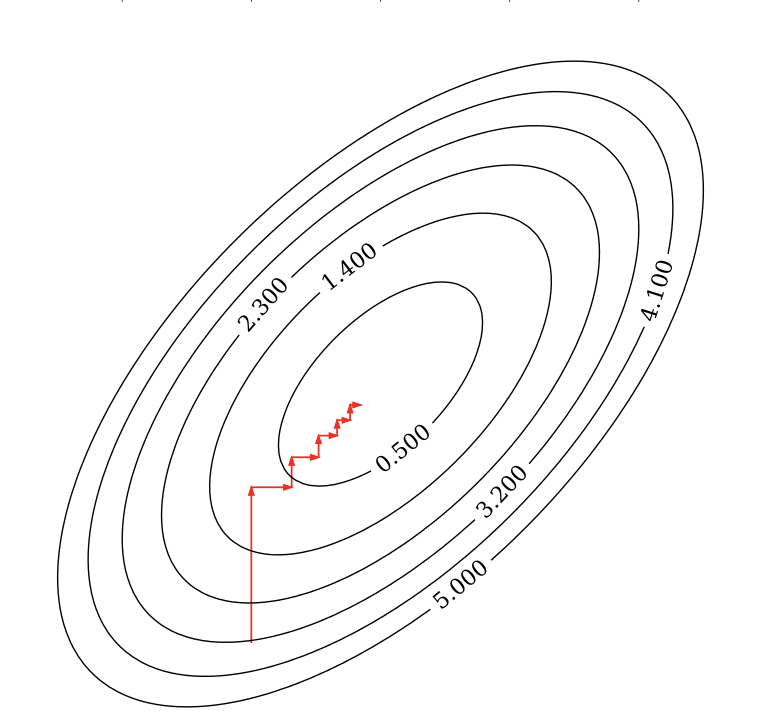
Coordinate descent with Lasso¶
Remember that $\mathcal{L}_{Lasso} = \mathcal{L}_{SSE} + \alpha \sum_{i=1}^{p} |w_i|$
For one $w_i$: $\mathcal{L}_{Lasso}(w_i) = \mathcal{L}_{SSE}(w_i) + \alpha |w_i|$
The L1 term is not differentiable but convex: we can compute the subgradient
Unique at points where $\mathcal{L}$ is differentiable, a range of all possible slopes [a,b] where it is not
For $|w_i|$, the subgradient $\partial_{w_i} |w_i|$ = $\begin{cases}-1 & w_i<0\\ [-1,1] & w_i=0 \\ 1 & w_i>0 \\ \end{cases}$
Subdifferential $\partial(f+g) = \partial f + \partial g$ if $f$ and $g$ are both convex
To find the optimum for Lasso $w_i^{*}$, solve
$$\begin{aligned} \partial_{w_i} \mathcal{L}_{Lasso}(w_i) &= \partial_{w_i} \mathcal{L}_{SSE}(w_i) + \partial_{w_i} \alpha |w_i| \\ 0 &= (w_i - \rho_i) + \alpha \cdot \partial_{w_i} |w_i| \\ w_i &= \rho_i - \alpha \cdot \partial_{w_i} |w_i| \end{aligned}$$
- In which $\rho_i$ is the part of $\partial_{w_i} \mathcal{L}_{SSE}(w_i)$ excluding $w_i$ (assume $z_i=1$ for now)
- $\rho_i$ can be seen as the $\mathcal{L}_{SSE}$ 'solution': $w_i = \rho_i$ if $\partial_{w_i} \mathcal{L}_{SSE}(w_i) = 0$ $$\partial_{w_i} \mathcal{L}_{SSE}(w_i) = \partial_{w_i} \sum_{n=1}^{N} (y_n-(\mathbf{w}\mathbf{x_n} + w_0))^2 = z_i w_i -\rho_i $$
- In which $\rho_i$ is the part of $\partial_{w_i} \mathcal{L}_{SSE}(w_i)$ excluding $w_i$ (assume $z_i=1$ for now)
We found: $w_i = \rho_i - \alpha \cdot \partial_{w_i} |w_i|$
The Lasso solution has the form of a soft thresholding function $S$
$$w_i^* = S(\rho_i,\alpha) = \begin{cases} \rho_i + \alpha, & \rho_i < -\alpha \\ 0, & -\alpha < \rho_i < \alpha \\ \rho_i - \alpha, & \rho_i > \alpha \\ \end{cases}$$
- Small weights (all weights between $-\alpha$ and $\alpha$) become 0: sparseness!
- If the data is not normalized, $w_i^* = \frac{1}{z_i}S(\rho_i,\alpha)$ with constant $z_i = \sum_{n=1}^{N} x_{ni}^2$
Ridge solution: $w_i = \rho_i - \alpha \cdot \partial_{w_i} w_i^2 = \rho_i - 2\alpha \cdot w_i$, thus $w_i^* = \frac{\rho_i}{1 + 2\alpha}$
interactive(children=(FloatSlider(value=1.0, description='alpha', max=2.0, step=0.05), Output()), _dom_classes…
Least Squares Loss + L1 or L2
- The Lasso curve has 3 parts ($w<0$,$w=0$,$w>0$) corresponding to the thresholding function
- For any minimum of least squares, L2 will be smaller, and L1 is more likely be exactly 0
interactive(children=(FloatSlider(value=0.5, description='alpha', max=1.0, step=0.05), Output()), _dom_classes…
- In 2D (for 2 model weights $w_1$ and $w_2$)
- The least squared loss is a 2D convex function in this space (ellipses on the right)
- For illustration, assume that L1 loss = L2 loss = 1
- L1 loss ($\Sigma |w_i|$): the optimal {$w_1, w_2$} (blue dot) falls on the diamond
- L2 loss ($\Sigma w_i^2$): the optimal {$w_1, w_2$} (cyan dot) falls on the circle
- For L1, the loss is minimized if $w_1$ or $w_2$ is 0 (rarely so for L2)
Elastic-Net¶
- Adds both L1 and L2 regularization:
$$\mathcal{L}_{Elastic} = \sum_{n=1}^{N} (y_n-(\mathbf{w}\mathbf{x_n} + w_0))^2 + \alpha \rho \sum_{i=1}^{p} |w_i| + \alpha (1 - \rho) \sum_{i=1}^{p} w_i^2$$
- $\rho$ is the L1 ratio
- With $\rho=1$, $\mathcal{L}_{Elastic} = \mathcal{L}_{Lasso}$
- With $\rho=0$, $\mathcal{L}_{Elastic} = \mathcal{L}_{Ridge}$
- $0 < \rho < 1$ sets a trade-off between L1 and L2.
- Allows learning sparse models (like Lasso) while maintaining L2 regularization benefits
- E.g. if 2 features are correlated, Lasso likely picks one randomly, Elastic-Net keeps both
- Weights can be optimized using coordinate descent (similar to Lasso)
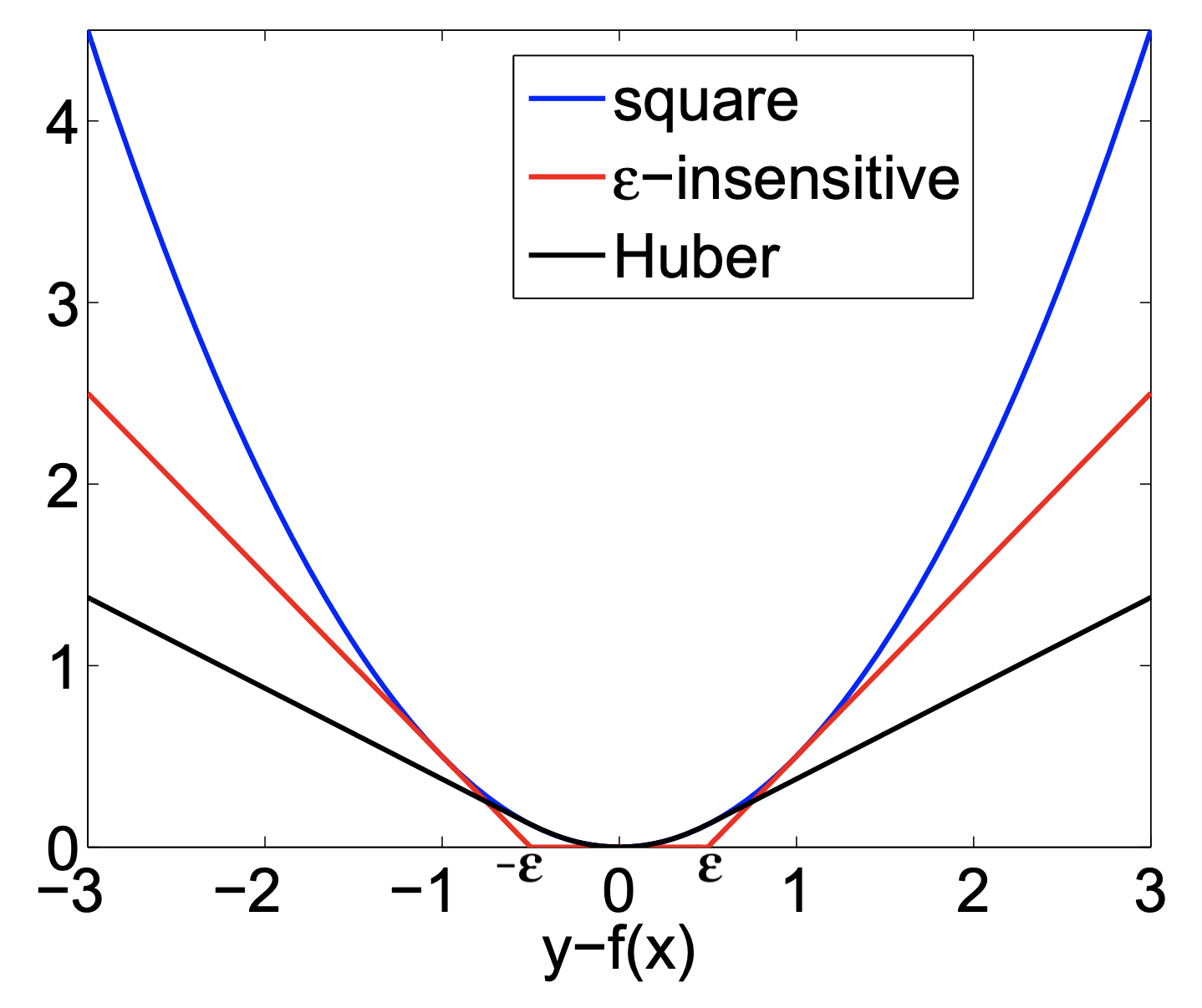
Other loss functions for regression¶
- Huber loss: switches from squared loss to linear loss past a value $\epsilon$
- More robust against outliers
- Epsilon insensitive: ignores errors smaller than $\epsilon$, and linear past that
- Aims to fit function so that residuals are at most $\epsilon$
- Also known as Support Vector Regression (
SVRin sklearn)
- Squared Epsilon insensitive: ignores errors smaller than $\epsilon$, and squared past that
- These can all be solved with stochastic gradient descent
SGDRegressorin sklearn
Linear models for Classification¶
Aims to find a hyperplane that separates the examples of each class.
For binary classification (2 classes), we aim to fit the following function:
$\hat{y} = w_1 * x_1 + w_2 * x_2 +... + w_p * x_p + w_0 > 0$
When $\hat{y}<0$, predict class -1, otherwise predict class +1
There are many algorithms for linear classification, differing in loss function, regularization techniques, and optimization method
Most common techniques:
- Convert target classes {neg,pos} to {0,1} and treat as a regression task
- Logistic regression (Log loss)
- Ridge Classification (Least Squares + L2 loss)
- Find hyperplane that maximizes the margin between classes
- Linear Support Vector Machines (Hinge loss)
- Neural networks without activation functions
- Perceptron (Perceptron loss)
- SGDClassifier: can act like any of these by choosing loss function
- Hinge, Log, Modified_huber, Squared_hinge, Perceptron
- Convert target classes {neg,pos} to {0,1} and treat as a regression task
Logistic regression¶
Aims to predict the probability that a point belongs to the positive class
Converts target values {negative (blue), positive (red)} to {0,1}
Fits a logistic (or sigmoid or S curve) function through these points
- Maps (-Inf,Inf) to a probability [0,1]
$$ \hat{y} = \textrm{logistic}(f_{\theta}(\mathbf{x})) = \frac{1}{1+e^{-f_{\theta}(\mathbf{x})}} $$
E.g. in 1D: $ \textrm{logistic}(x_1w_1+w_0) = \frac{1}{1+e^{-x_1w_1-w_0}} $
interactive(children=(FloatSlider(value=-3.0, description='w0', max=5.0, min=-10.0, step=1.0), FloatSlider(val…
- Fitted solution to our 2D example:
- To get a binary prediction, choose a probability threshold (e.g. 0.5)
interactive(children=(IntSlider(value=180, description='rotation', max=360, step=10), Output()), _dom_classes=…
Loss function: Cross-entropy¶
Models that return class probabilities can use cross-entropy loss
$$\mathcal{L_{log}}(\mathbf{w}) = \sum_{n=1}^{N} H(p_n,q_n) = - \sum_{n=1}^{N} \sum_{c=1}^{C} p_{n,c} log(q_{n,c}) $$
- Also known as log loss, logistic loss, or maximum likelihood
- Based on true probabilities $p$ (0 or 1) and predicted probabilities $q$ over $N$ instances and $C$ classes
- Binary case (C=2): $\mathcal{L_{log}}(\mathbf{w}) = - \sum_{n=1}^{N} \big[ y_n log(\hat{y}_n) + (1-y_n) log(1-\hat{y}_n) \big]$
- Penalty (a.k.a. 'surprise') grows exponentially as difference between $p$ and $q$ increases
- If you are sure of an answer (high $q$) and it's wrong (low $p$), you definitely want to learn
- Often used together with L2 (or L1) loss: $\mathcal{L_{log}}'(\mathbf{w}) = \mathcal{L_{log}}(\mathbf{w}) + \alpha \sum_{i} w_i^2 $
Optimization methods (solvers) for cross-entropy loss¶
- Gradient descent (only supports L2 regularization)
- Log loss is differentiable, so we can use (stochastic) gradient descent
- Variants thereof, e.g. Stochastic Average Gradient (SAG, SAGA)
- Coordinate descent (supports both L1 and L2 regularization)
- Faster iteration, but may converge more slowly, has issues with saddlepoints
- Called
liblinearin sklearn. Can't run in parallel.
- Newton-Rhapson or Newton Conjugate Gradient (only L2):
- Uses the Hessian $H = \big[\frac{\partial^2 \mathcal{L}}{\partial x_i \partial x_j} \big]$: $\mathbf{w}^{s+1} = \mathbf{w}^s-\eta H^{-1}(\mathbf{w}^s) \nabla \mathcal{L}(\mathbf{w}^s)$
- Slow for large datasets. Works well if solution space is (near) convex
- Quasi-Newton methods (only L2)
- Approximate, faster to compute
- E.g. Limited-memory Broyden–Fletcher–Goldfarb–Shanno (
lbfgs)- Default in sklearn for Logistic Regression
- Some hints on choosing solvers
- Data scaling helps convergence, minimizes differences between solvers
In practice¶
- Logistic regression can also be found in
sklearn.linear_model.Chyperparameter is the inverse regularization strength: $C=\alpha^{-1}$penalty: type of regularization: L1, L2 (default), Elastic-Net, or Nonesolver: newton-cg, lbfgs (default), liblinear, sag, saga
- Increasing C: less regularization, tries to overfit individual points
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C=1).fit(X_train, y_train)
interactive(children=(FloatSlider(value=0.0, description='C_log', max=4.0, min=-3.0), Output()), _dom_classes=…
- Analyze behavior on the breast cancer dataset
- Underfitting if C is too small, some overfitting if C is too large
- We use cross-validation because the dataset is small
- Again, choose between L1 or L2 regularization (or elastic-net)
- Small C overfits, L1 leads to sparse models
interactive(children=(FloatSlider(value=499.91, description='C', max=1000.0, min=0.01), Dropdown(description='…
Ridge Classification¶
Instead of log loss, we can also use ridge loss:
$$\mathcal{L}_{Ridge} = \sum_{n=1}^{N} (y_n-(\mathbf{w}\mathbf{x_n} + w_0))^2 + \alpha \sum_{i=1}^{p} w_i^2$$
In this case, target values {negative, positive} are converted to {-1,1}
Can be solved similarly to Ridge regression:
- Closed form solution (a.k.a. Cholesky)
- Gradient descent and variants
- E.g. Conjugate Gradient (CG) or Stochastic Average Gradient (SAG,SAGA)
- Use Cholesky for smaller datasets, Gradient descent for larger ones
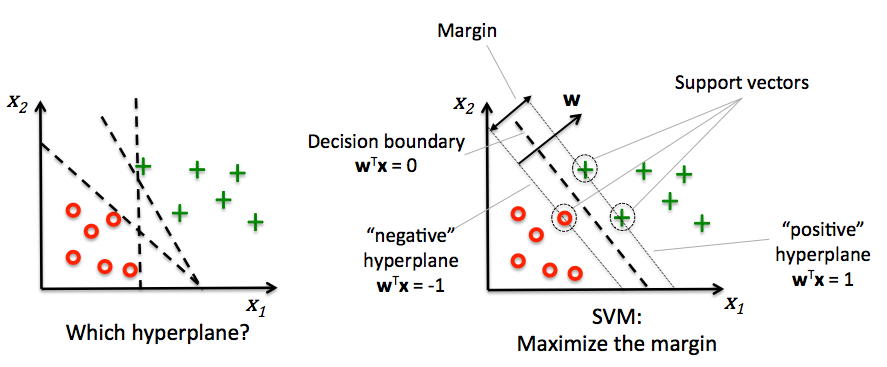
Support vector machines¶
- Decision boundaries close to training points may generalize badly
- Very similar (nearby) test point are classified as the other class
- Choose a boundary that is as far away from training points as possible
- The support vectors are the training samples closest to the hyperplane
- The margin is the distance between the separating hyperplane and the support vectors
- Hence, our objective is to maximize the margin
Solving SVMs with Lagrange Multipliers¶
- Imagine a hyperplane (green) $y= \sum_1^p \mathbf{w}_i * \mathbf{x}_i + w_0$ that has slope $\mathbf{w}$, value '+1' for the positive (red) support vectors, and '-1' for the negative (blue) ones
- Margin between the boundary and support vectors is $\frac{y-w_0}{||\mathbf{w}||}$, with $||\mathbf{w}|| = \sum_i^p w_i^2$
- We want to find the weights that maximize $\frac{1}{||\mathbf{w}||}$. We can also do that by maximizing $\frac{1}{||\mathbf{w}||^2}$
interactive(children=(IntSlider(value=10, description='rotationX', max=20), IntSlider(value=135, description='…
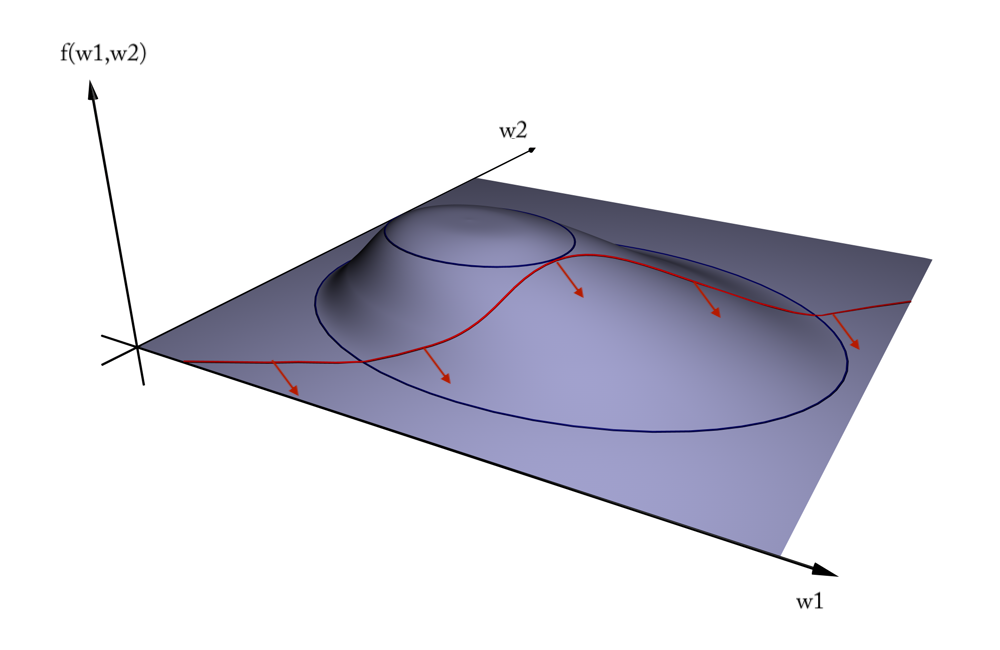
Geometric interpretation¶
- We want to maximize $f = \frac{1}{||w||^2}$ (blue contours)
- The hyperplane (red) must be $> 1$ for all positive examples:
$g(\mathbf{w}) = \mathbf{w} \mathbf{x_i} + w_0 > 1 \,\,\, \forall{i}, y(i)=1$ - Find the weights $\mathbf{w}$ that satify $g$ but maximize $f$
Solution¶
- A quadratic loss function with linear constraints can be solved with Lagrangian multipliers
- This works by assigning a weight $a_i$ (called a dual coefficient) to every data point $x_i$
- They reflect how much individual points influence the weights $\mathbf{w}$
- The points with non-zero $a_i$ are the support vectors
- Next, solve the following Primal objective:
- $y_i=\pm1$ is the correct class for example $x_i$
$$\mathcal{L}_{Primal} = \frac{1}{2} ||\mathbf{w}||^2 - \sum_{i=1}^{n} a_i y_i (\mathbf{w} \mathbf{x_i} + w_0) + \sum_{i=1}^{n} a_i $$
so that
$$ \mathbf{w} = \sum_{i=1}^{n} a_i y_i \mathbf{x_i} $$ $$ a_i \geq 0 \quad \text{and} \quad \sum_{i=1}^{l} a_i y_i = 0 $$
- It has a Dual formulation as well (See 'Elements of Statistical Learning' for the full derivation):
$$\mathcal{L}_{Dual} = \sum_{i=1}^{l} a_i - \frac{1}{2} \sum_{i,j=1}^{l} a_i a_j y_i y_j (\mathbf{x_i} \mathbf{x_j}) $$
so that
$$ a_i \geq 0 \quad \text{and} \quad \sum_{i=1}^{l} a_i y_i = 0 $$
Computes the dual coefficients directly. A number $l$ of these are non-zero (sparseness).
- Dot product $\mathbf{x_i} \mathbf{x_j}$ can be interpreted as the closeness between points $\mathbf{x_i}$ and $\mathbf{x_j}$
- We can replace the dot product with other similarity functions (kernels)
- $\mathcal{L}_{Dual}$ increases if nearby support vectors $\mathbf{x_i}$ with high weights $a_i$ have different class $y_i$
- $\mathcal{L}_{Dual}$ also increases with the number of support vectors $l$ and their weights $a_i$
- Dot product $\mathbf{x_i} \mathbf{x_j}$ can be interpreted as the closeness between points $\mathbf{x_i}$ and $\mathbf{x_j}$
Can be solved with quadratic programming, e.g. Sequential Minimal Optimization (SMO)
Example result. The circled samples are support vectors, together with their coefficients.
Making predictions¶
$a_i$ will be 0 if the training point lies on the right side of the decision boundary and outside the margin
- The training samples for which $a_i$ is not 0 are the support vectors
Hence, the SVM model is completely defined by the support vectors and their dual coefficients (weights)
Knowing the dual coefficients $a_i$, we can find the weights $w$ for the maximal margin separating hyperplane
- And we could classify a new sample $\mathbf{u}$ by looking at the sign of $\mathbf{w}\mathbf{u}+w_0$
$$ \mathbf{w} = \sum_{i=1}^{l} a_i y_i \mathbf{x_i} $$
- However, we don't need to compute $\mathbf{w}$ to make predictions. We only need to look at the support vectors.
SVMs and kNN¶
- Remember, we will classify a new point $\mathbf{u}$ by looking at the sign of:
$$f(x) = \mathbf{w}\mathbf{u}+w_0 = \sum_{i=1}^{l} a_i y_i \mathbf{x_i}\mathbf{u}+w_0$$
- Weighted k-nearest neighbor is a generalization of the k-nearest neighbor classifier. It classifies points by evaluating:
$$f(x) = \sum_{i=1}^{k} a_i y_i dist(x_i, u)^{-1}$$
- Hence: SVM's predict much the same way as k-NN, only:
- They only consider the truly important points (the support vectors): much faster
- The number of neighbors is the number of support vectors
- The distance function is an inner product of the inputs (or another kernel)
- They only consider the truly important points (the support vectors): much faster
- Given $\mathbf{u}$, we predict by looking at the classes of the support vectors, weighted by their distance.
Regularized (soft margin) SVMs¶
If the data is not linearly separable, (hard) margin maximization becomes meaningless
Relax the contraint by allowing an error $\xi_{i}$: $y_i (\mathbf{w}\mathbf{x_i} + w_0) \geq 1 - \xi_{i}$
Or (since $\xi_{i} \geq 0$): $\xi_{i} = max(0,1-y_i\cdot(\mathbf{w}\mathbf{x_i} + w_0))$
The sum over all points is called hinge loss: $\sum_i^n \xi_{i}$
Attenuating the error component with a hyperparameter $C$, we get the objective
$$\mathcal{L}(\mathbf{w}) = ||\mathbf{w}||^2 + C \sum_i^n \xi_{i}$$
- Can still be solved with quadratic programming
Effect of regularization on margin and support vectors¶
- SVM's Hinge loss acts like L1 regularization, yields sparse models
- C is the inverse regularization strength (inverse of $\alpha$ in Lasso)
- Larger C: fewer support vectors, smaller margin, more overfitting
- Smaller C: more support vectors, wider margin, less overfitting
- Needs to be tuned carefully to the data
Same for non-linearly separable data
Large C values can lead to overfitting (e.g. fitting noise), small values can lead to underfitting
Kernelization¶
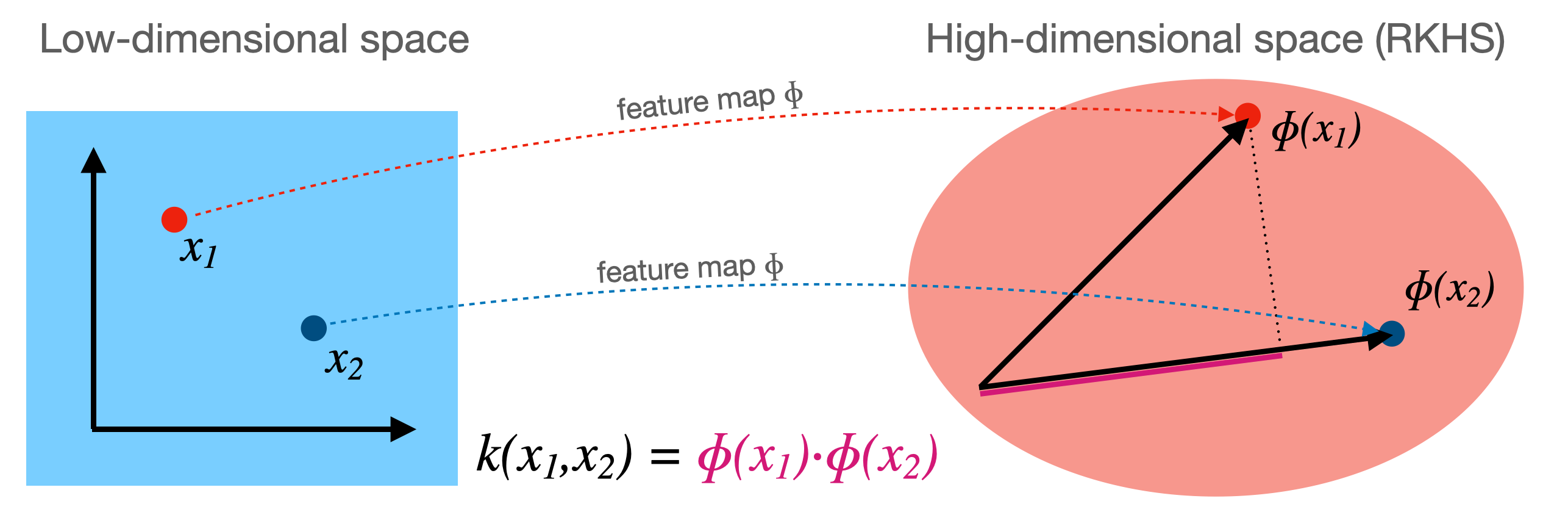
- Sometimes we can separate the data better by first transforming it to a higher dimensional space $\Phi(x)$
- This transformation $\Phi$ is called a feature map (but can be expensive)
- For certain $\Phi$, we know the function $k$ that computes the dot product in $\Phi(x)$: $ k(\mathbf{x_i},\mathbf{x_j}) = \Phi(\mathbf{x_i}) \cdot \Phi(\mathbf{x_j})$
- This kernel function $k(\mathbf{x_i},\mathbf{x_j})$ computes the dot product without having to construct (reproduce) $\Phi(x)$
- Kernel trick: if your loss function has a dot product, you can simply replace it with a kernel!
- For SVMs (in dual form), replacing $(\mathbf{x_i}\mathbf{x_j}) \rightarrow k(\mathbf{x_i},\mathbf{x_j})$ yields a kernelized SVM: $$\mathcal{L}_{Dual} (a_i, k) = \sum_{i=1}^{l} a_i - \frac{1}{2} \sum_{i,j=1}^{l} a_i a_j y_i y_j k(\mathbf{x_i},\mathbf{x_j}) $$
Polynomial kernel¶
- The polynomial kernel (for degree $d \in \mathbb{N}$) reproduces the polynomial feature map
$$[1, x_1, ..., x_p] \xrightarrow{\phi} [1, x_1, ..., x_p, x_1^2, ..., x_p^2, ..., x_p^d, x_1 x_2, ..., x_{p-1} x_p]$$
- It can be easily computed from the original dot product:
$$k_{poly}(\mathbf{x_1},\mathbf{x_2}) = (\gamma (\mathbf{x_1} \cdot \mathbf{x_2}) + c_0)^d$$
- It has two more hyperparameters, but you can usually leave them at default
- $\gamma$ is a scaling hyperparameter (default $\frac{1}{p}$)
- $c_0$ is a hyperparameter (default 1) to trade off influence of higher-order terms
- By simply replacing the dot product with a kernel we can learn non-linear SVMs!
- It is technically still linear in $\Phi(x)$, but in our original space the boundary becomes a polynomial curve
- Prediction still happens as before, but the influence of each support vector drops of polynomially (with degree $d$)
Radial Basis Function (RBF) kernel¶
- The RBF or Gaussian kernel (of width $\gamma > 0$) is related to the Taylor series expansion of $e^x$
$$\Phi(x) = e^{-x^2/2\gamma^2} \Big[ 1, \sqrt{\frac{1}{1!\gamma^2}}x,\sqrt{\frac{1}{2!\gamma^4}}x^2,\sqrt{\frac{1}{3!\gamma^6}}x^3,\ldots\Big]^T$$
- It is a function of how closely together two data points are:
$$k_{RBF}(\mathbf{x_1},\mathbf{x_2}) = exp(-\gamma ||\mathbf{x_1} - \mathbf{x_2}||^2)$$
- The influence of a point $\mathbf{x_2}$ on point $\mathbf{x_1}$ drops off exponentially with its distance to $\mathbf{x_1}$
- The influence of each support vector now drops of exponentially
- Hence, predictions are only affected by very nearby support vectors
- RBF kernels are therefore called local kernels
- The kernel width ($\gamma$) defines how sharply the local influence decays
- Acts as a regularizer: low $\gamma$ causes underfitting and high $\gamma$ causes overfitting
- SVM's C parameter (inverse regularizer) is still at play and thus interacts with $\gamma$
interactive(children=(FloatSlider(value=4.6, description='gamma', max=10.0, min=0.1, step=0.5), FloatSlider(va…
Kernelization sidenotes (optional)¶
- You can invent many more feature maps and corresponding kernels (eg. for text, graphs,...)
- However, learning deep learning embeddings from lots of data often works better
- You can also kernelize Ridge regression, Logistic regression, Perceptrons, Support Vector Regression,...
- The Representer theorem will give you the corresponding loss function
- For more detail see the Kernelization lecture under extra materials.
SVMs in scikit-learn¶
svm.LinearSVC: faster for large datasets- Allows choosing between the primal or dual. Primal recommended when $n$ >> $p$
- Returns
coef_($\mathbf{w}$) andintercept_($w_0$)
svm.SVCallows different kernels to be used- Also returns
support_vectors_(the support vectors) and thedual_coef_$a_i$ - Scales at least quadratically with the number of samples $n$
- Also returns
svm.LinearSVRandsvm.SVRare variants for regression
clf = svm.SVC(kernel='linear') # or 'RBF' or 'Poly'
clf.fit(X, Y)
print("Support vectors:", clf.support_vectors_[:])
print("Coefficients:", clf.dual_coef_[:])
Support vectors: [[-1.021 0.241] [-0.467 -0.531] [ 0.951 0.58 ]] Coefficients: [[-0.048 -0.569 0.617]]
Solving SVMs with Gradient Descent¶
- SVMs can, alternatively, be solved using gradient decent
- Good for large datasets, but does not yield support vectors or kernelization
- Hinge loss is not differentiable but convex, and has a subgradient:
$$\mathcal{L_{Hinge}}(\mathbf{w}) = max(0,1-y_i (\mathbf{w}\mathbf{x_i} + w_0))$$
$$\frac{\partial \mathcal{L_{Hinge}}}{\partial w_i} = \begin{cases}-y_i x_i & y_i (\mathbf{w}\mathbf{x_i} + w_0) < 1\\ 0 & \text{otherwise} \\ \end{cases}$$
- Can be solved with (stochastic) gradient descent
Generalized SVMs¶
- There are many smoothed versions of hinge loss:
- Squared hinge loss:
- Also known as Ridge classification
- Least Squares SVM: allows kernelization (using a linear equation solver)
- Modified Huber loss: squared hinge, but linear after -1. Robust against outliers
- Log loss: equivalent to logistic regression
- Squared hinge loss:
- In sklearn,
SGDClassifiercan be used with any of these. Good for large datasets.
Perceptron¶
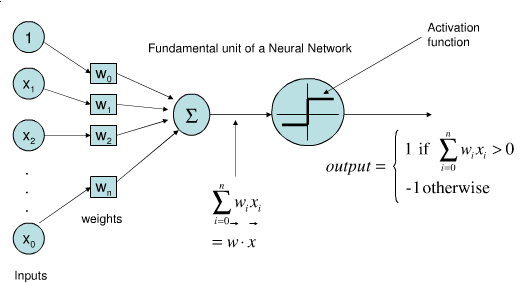
Represents a single neuron (node) with inputs $x_i$, a bias $w_0$, and output $y$
Each connection has a (synaptic) weight $w_i$. The node outputs $\hat{y} = \sum_{i}^n x_{i}w_i + w_0$
The activation function (neuron output) is 1 if $\mathbf{xw} + w_0 > 0$, -1 otherwise
Idea: Update synapses only on misclassification, correct output by exactly $\pm1$
Weights can be learned with (stochastic) gradient descent and Hinge(0) loss
$$\mathcal{L}_{Perceptron} = max(0,-y_i (\mathbf{w}\mathbf{x_i} + w_0))$$
$$\frac{\partial \mathcal{L_{Perceptron}}}{\partial w_i} = \begin{cases}-y_i x_i & y_i (\mathbf{w}\mathbf{x_i} + w_0) < 0\\ 0 & \text{otherwise} \\ \end{cases}$$
- Every binary classifiers makes a prediction, the one with the highest score (>0) wins
one-vs-one¶
- An alternative is to learn a binary model for every combination of two classes
- For $C$ classes, this results in $\frac{C(C-1)}{2}$ binary models
- Each point is classified according to a majority vote amongst all models
- Can also be a 'soft vote': sum up the probabilities (or decision values) for all models. The class with the highest sum wins.
- Requires more models than one-vs-rest, but training each one is faster
- Only the examples of 2 classes are included in the training data
- Recommended for algorithms than learn well on small datasets
- Especially SVMs and Gaussian Processes
Linear models overview¶
| Name | Representation | Loss function | Optimization | Regularization |
|---|---|---|---|---|
| Least squares | Linear function (R) | SSE | CFS or SGD | None |
| Ridge | Linear function (R) | SSE + L2 | CFS or SGD | L2 strength ($\alpha$) |
| Lasso | Linear function (R) | SSE + L1 | Coordinate descent | L1 strength ($\alpha$) |
| Elastic-Net | Linear function (R) | SSE + L1 + L2 | Coordinate descent | $\alpha$, L1 ratio ($\rho$) |
| SGDRegressor | Linear function (R) | SSE, Huber, $\epsilon$-ins,... + L1/L2 | SGD | L1/L2, $\alpha$ |
| Logistic regression | Linear function (C) | Log + L1/L2 | SGD, coordinate descent,... | L1/L2, $\alpha$ |
| Ridge classification | Linear function (C) | SSE + L2 | CFS or SGD | L2 strength ($\alpha$) |
| Linear SVM | Support Vectors | Hinge(1) | Quadratic programming or SGD | Cost (C) |
| Kernelized SVM | Support Vectors | Hinge(1) | Quadratic programming or SGD | Cost (C), $\gamma$,... |
| Least Squares SVM | Support Vectors | Squared Hinge | Linear equations or SGD | Cost (C) |
| Perceptron | Linear function (C) | Hinge(0) | SGD | None |
| SGDClassifier | Linear function (C) | Log, (Sq.) Hinge, Mod. Huber,... | SGD | L1/L2, $\alpha$ |
- SSE: Sum of Squared Errors
- CFS: Closed-form solution
- SGD: (Stochastic) Gradient Descent and variants
- (R)egression, (C)lassification
Summary¶
- Linear models
- Good for very large datasets (scalable)
- Good for very high-dimensional data (not for low-dimensional data)
- Can be used to fit non-linear or low-dim patterns as well (see later)
- Preprocessing: e.g. Polynomial or Poisson transformations
- Generalized linear models (kernelization)
- Regularization is important. Tune the regularization strength ($\alpha$)
- Ridge (L2): Good fit, sometimes sensitive to outliers
- Lasso (L1): Sparse models: fewer features, more interpretable, faster
- Elastic-Net: Trade-off between both, e.g. for correlated features
- Most can be solved by different optimizers (solvers)
- Closed form solutions or quadratic/linear solvers for smaller datasets
- Gradient descent variants (SGD,CD,SAG,CG,...) for larger ones
- Multi-class classification can be done using a one-vs-all approach