Why Machine Learning?¶
- Search engines (e.g. Google)
- Recommender systems (e.g. Netflix)
- Automatic translation (e.g. Google Translate)
- Speech understanding (e.g. Siri, Alexa)
- Game playing (e.g. AlphaGo)
- Self-driving cars
- Personalized medicine
- Progress in all sciences: Genetics, astronomy, chemistry, neurology, physics,...
What is Machine Learning?¶
- Learn to perform a task, based on experience (examples) $X$, minimizing error $\mathcal{E}$
- E.g. recognizing a person in an image as accurately as possible
- Often, we want to learn a function (model) $f$ with some model parameters $\theta$ that produces the right output $y$
- Usually part of a much larger system that provides the data $X$ in the right form
- Data needs to be collected, cleaned, normalized, checked for data biases,...
Inductive bias¶
- In practice, we have to put assumptions into the model: inductive bias $b$
- What should the model look like?
- Mimick human brain: Neural Networks
- Logical combination of inputs: Decision trees, Linear models
- Remember similar examples: Nearest Neighbors, SVMs
- Probability distribution: Bayesian models
- User-defined settings (hyperparameters)
- E.g. depth of tree, network architecture
- Assuptions about the data distribution, e.g. $X \sim N(\mu,\sigma)$
- What should the model look like?
- We can transfer knowledge from previous tasks: $f_1, f_2, f_3, ... \Longrightarrow f_{new}$
- Choose the right model, hyperparameters
- Reuse previously learned values for model parameters $\theta$
- In short:
Machine learning vs Statistics¶
- See Breiman (2001): Statistical modelling: The two cultures
Both aim to make predictions of natural phenomena:

Statistics:
- Help humans understand the world
- Assume data is generated according to an understandable model

Machine learning:
- Automate a task entirely (partially replace the human)
- Assume that the data generation process is unknown
- Engineering-oriented, less (too little?) mathematical theory
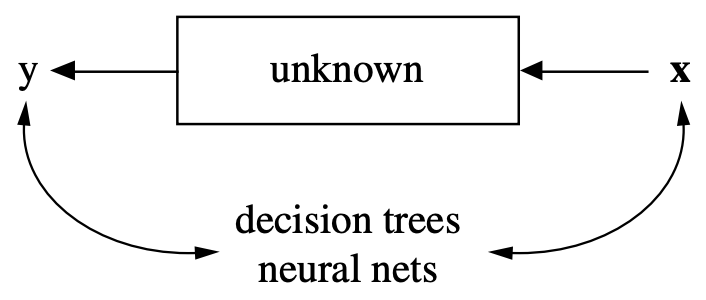
Types of machine learning¶
- Supervised Learning: learn a model $f$ from labeled data $(X,y)$ (ground truth)
- Given a new input X, predict the right output y
- Given examples of stars and galaxies, identify new objects in the sky
- Unsupervised Learning: explore the structure of the data (X) to extract meaningful information
- Given inputs X, find which ones are special, similar, anomalous, ...
- Semi-Supervised Learning: learn a model from (few) labeled and (many) unlabeled examples
- Unlabeled examples add information about which new examples are likely to occur
- Reinforcement Learning: develop an agent that improves its performance based on interactions with the environment
Note: Practical ML systems can combine many types in one system.
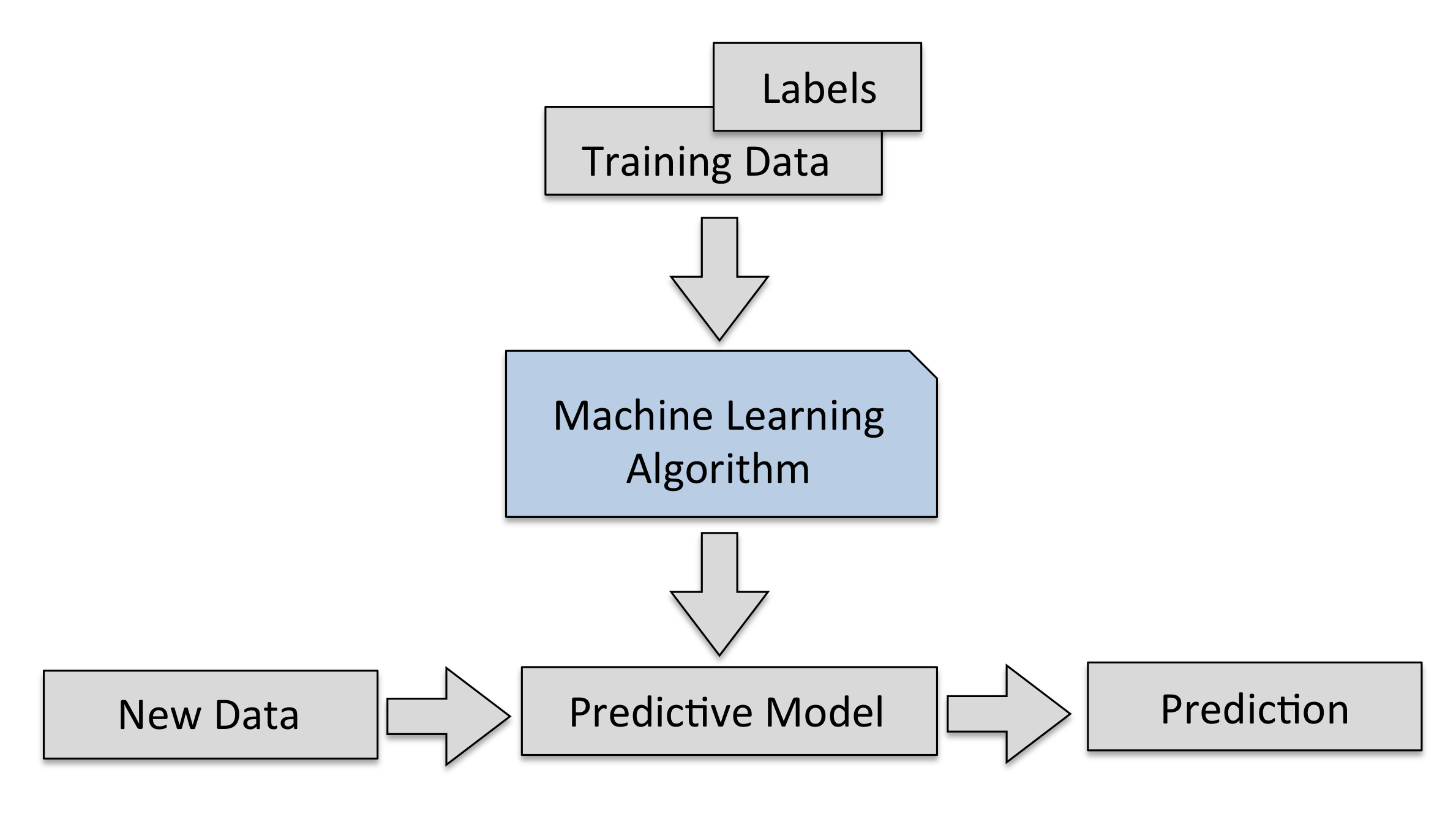
Supervised Machine Learning¶
- Learn a model from labeled training data, then make predictions
- Supervised: we know the correct/desired outcome (label)
- Subtypes: classification (predict a class) and regression (predict a numeric value)
- Most supervised algorithms that we will see can do both
Classification¶
- Predict a class label (category), discrete and unordered
- Can be binary (e.g. spam/not spam) or multi-class (e.g. letter recognition)
- Many classifiers can return a confidence per class
- The predictions of the model yield a decision boundary separating the classes
interactive(children=(Dropdown(description='classifier', options=(LogisticRegression(), SVC(gamma=2, probabili…
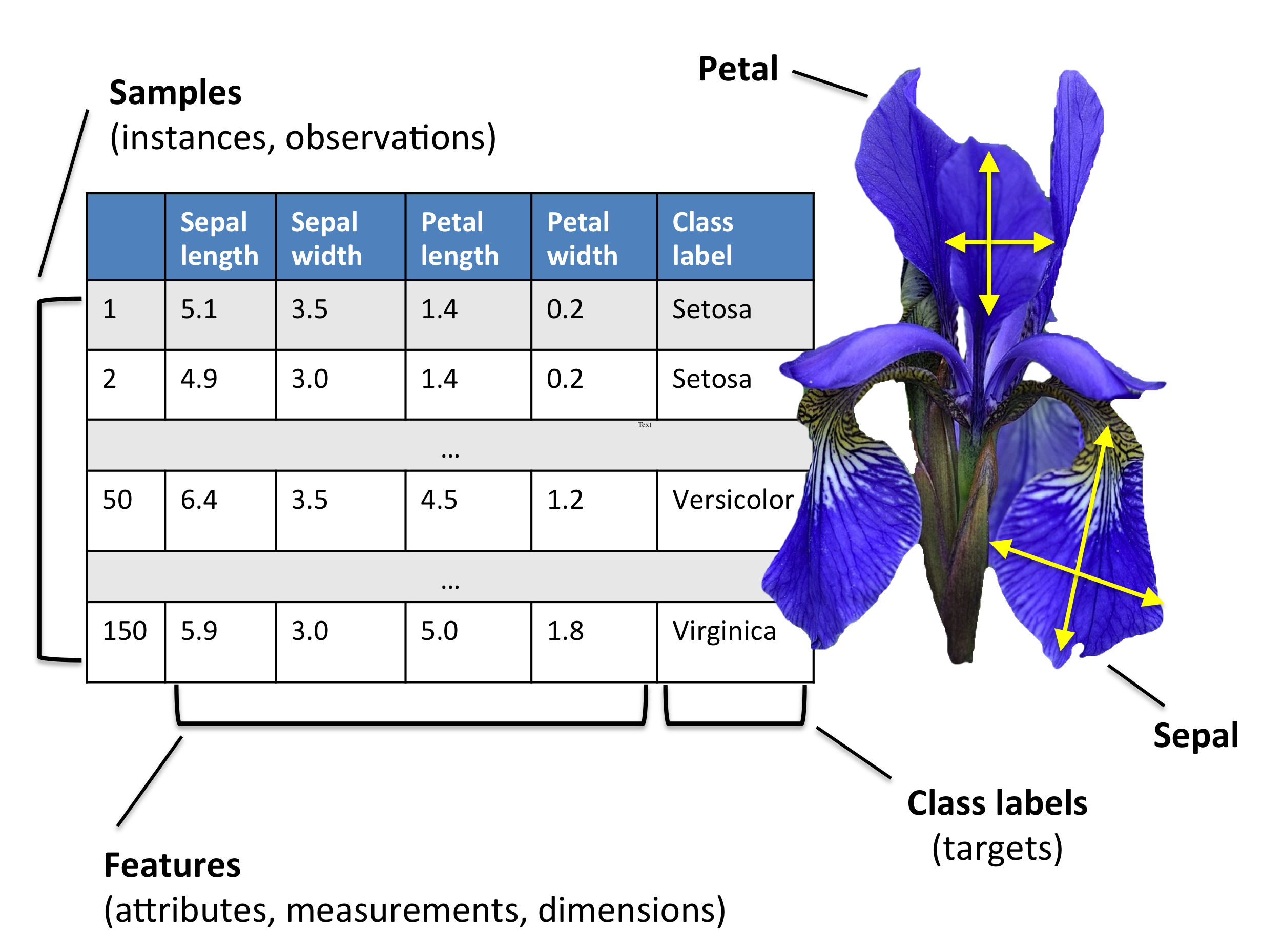
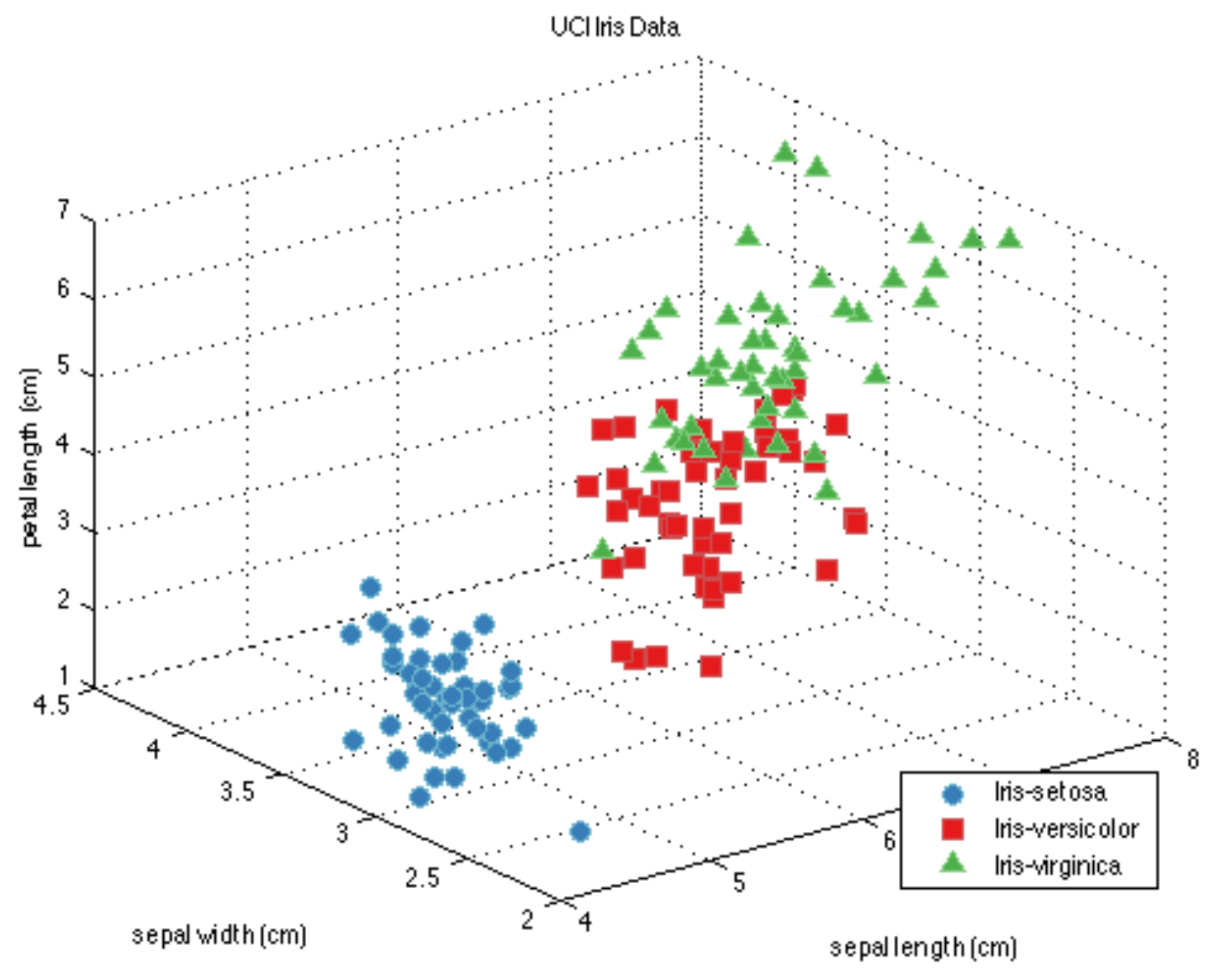
Example: Flower classification¶
Classify types of Iris flowers (setosa, versicolor, or virginica). How would you do it?

Representation: input features and labels¶
- We could take pictures and use them (pixel values) as inputs (-> Deep Learning)
- We can manually define a number of input features (variables), e.g. length and width of leaves
- Every `example' is a point in a (possibly high-dimensional) space
Regression¶
- Predict a continuous value, e.g. temperature
- Target variable is numeric
- Some algorithms can return a confidence interval
- Find the relationship between predictors and the target.
interactive(children=(Dropdown(description='regressor', options=(LinearRegression(), BayesianRidge(), Gaussian…
Unsupervised Machine Learning¶
- Unlabeled data, or data with unknown structure
- Explore the structure of the data to extract information
- Many types, we'll just discuss two.
Clustering¶
- Organize information into meaningful subgroups (clusters)
- Objects in cluster share certain degree of similarity (and dissimilarity to other clusters)
- Example: distinguish different types of customers
interactive(children=(IntSlider(value=50, description='randomize', min=1), Output()), _dom_classes=('widget-in…
Dimensionality reduction¶
- Data can be very high-dimensional and difficult to understand, learn from, store,...
- Dimensionality reduction can compress the data into fewer dimensions, while retaining most of the information
- Contrary to feature selection, the new features lose their (original) meaning
- The new representation can be a lot easier to model (and visualize)
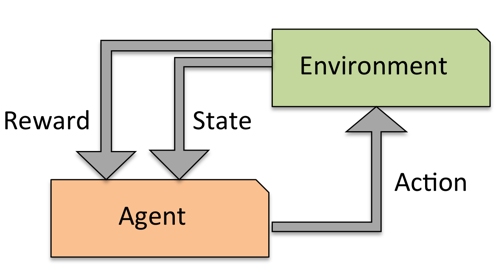
Reinforcement learning¶
- Develop an agent that improves its performance based on interactions with the environment
- Example: games like Chess, Go,...
- Search a (large) space of actions and states
- Reward function defines how well a (series of) actions works
- Learn a series of actions (policy) that maximizes reward through exploration
Learning = Representation + evaluation + optimization¶
All machine learning algorithms consist of 3 components:
- Representation: A model $f_{\theta}$ must be represented in a formal language that the computer can handle
- Defines the 'concepts' it can learn, the hypothesis space
- E.g. a decision tree, neural network, set of annotated data points
- Evaluation: An internal way to choose one hypothesis over the other
- Objective function, scoring function, loss function $\mathcal{L}(f_{\theta})$
- E.g. Difference between correct output and predictions
- Optimization: An efficient way to search the hypothesis space
- Start from simple hypothesis, extend (relax) if it doesn't fit the data
- Start with initial set of model parameters, gradually refine them
- Many methods, differing in speed of learning, number of optima,...
A powerful/flexible model is only useful if it can also be optimized efficiently
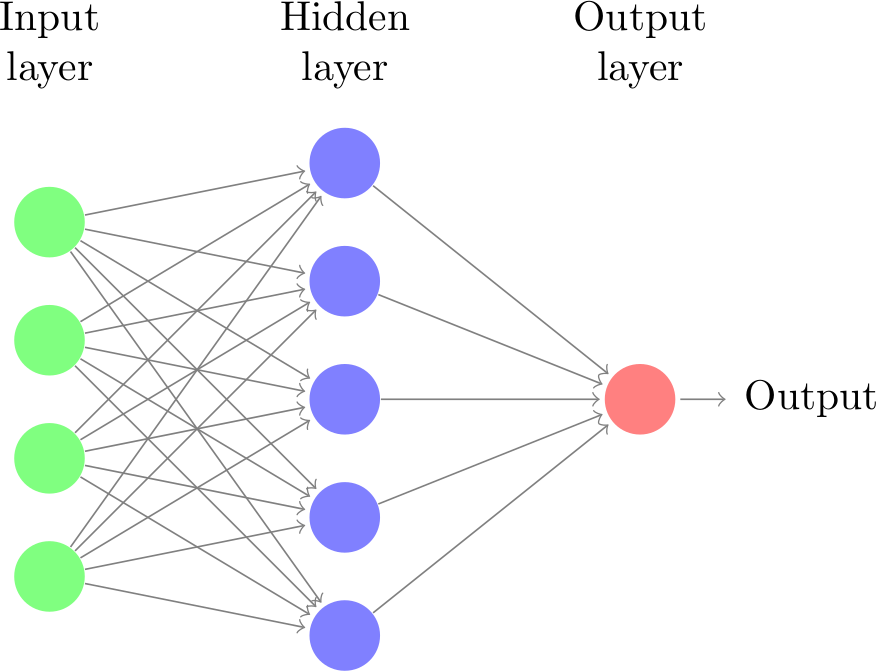
Neural networks: representation¶
Let's take neural networks as an example
- Representation: (layered) neural network
- Each connection has a weight $\theta_i$ (a.k.a. model parameters)
- Each node receives weighted inputs, emits new value
- Model $f$ returns the output of the last layer
- The architecture, number/type of neurons, etc. are fixed
- We call these hyperparameters (set by user, fixed during training)
Neural networks: evaluation and optimization¶
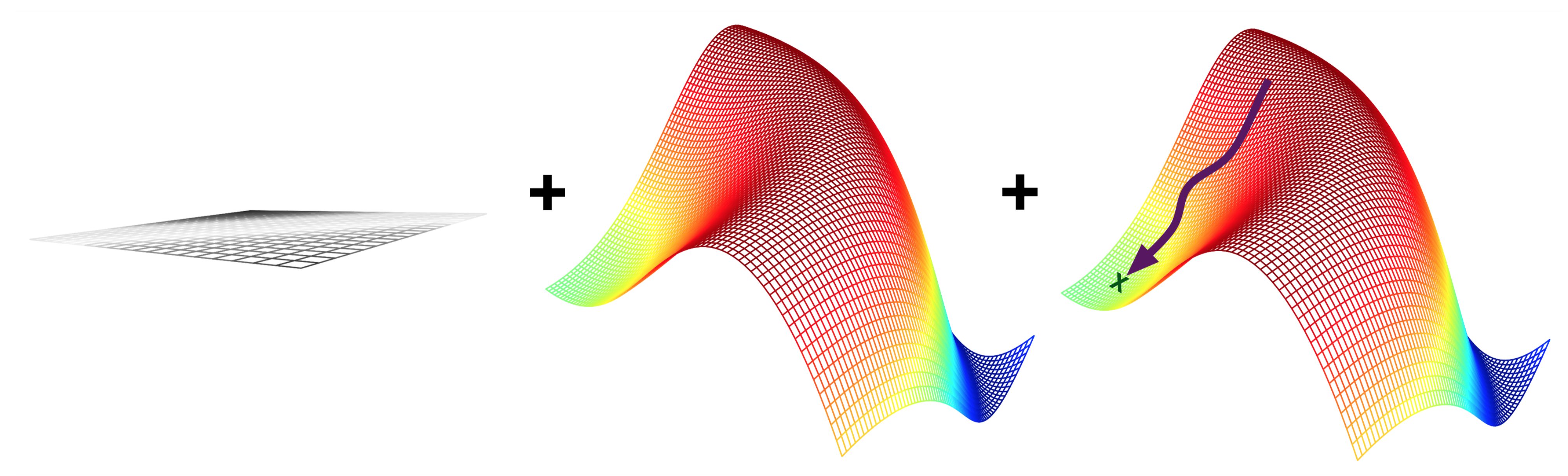
- Representation: Given the structure, the model is represented by its parameters
- Imagine a mini-net with two weights ($\theta_0,\theta_1$): a 2-dimensional search space
- Evaluation: A loss function $\mathcal{L}(f_{\theta})$ computes how good the predictions are
- Estimated on a set of training data with the 'correct' predictions
- We can't see the full surface, only evaluate specific sets of parameters
- Optimization: Find the optimal set of parameters
- Usually a type of search in the hypothesis space
- E.g. Gradient descent: $\theta_i^{new} = \theta_i + \frac{\mathcal{L}(f_{\theta})}{\partial \theta_i} $
Overfitting and Underfitting¶
- It's easy to build a complex model that is 100% accurate on the training data, but very bad on new data
- Overfitting: building a model that is too complex for the amount of data you have
- You model peculiarities in your training data (noise, biases,...)
- Solve by making model simpler (regularization), or getting more data
- Most algorithms have hyperparameters that allow regularization
- Underfitting: building a model that is too simple given the complexity of the data
- Use a more complex model
- There are techniques for detecting overfitting (e.g. bias-variance analysis). More about that later
- You can build ensembles of many models to overcome both underfitting and overfitting
- There is often a sweet spot that you need to find by optimizing the choice of algorithms and hyperparameters, or using more data.
- Example: regression using polynomial functions
interactive(children=(IntSlider(value=8, description='degrees', max=16, min=1), Output()), _dom_classes=('widg…
Model selection¶
- Next to the (internal) loss function, we need an (external) evaluation function
- Feedback signal: are we actually learning the right thing?
- Are we under/overfitting?
- Carefully choose to fit the application.
- Needed to select between models (and hyperparameter settings)
- Feedback signal: are we actually learning the right thing?
© XKCD

- Data needs to be split into training and test sets
- Optimize model parameters on the training set, evaluate on independent test set
- Avoid data leakage:
- Never optimize hyperparameter settings on the test data
- Never choose preprocessing techniques based on the test data
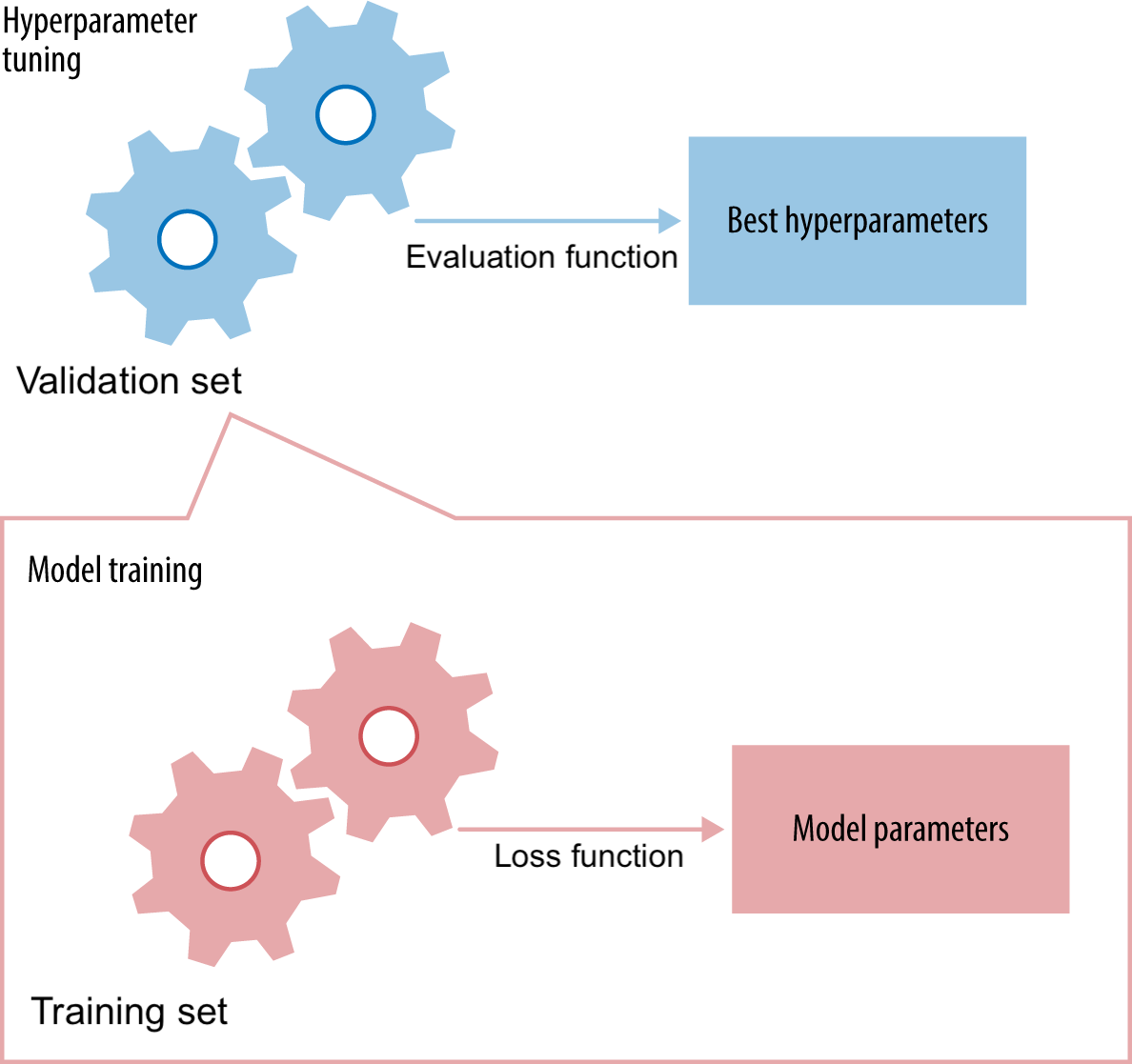
- To optimize hyperparameters and preprocessing as well, set aside part of training set as a validation set
- Keep test set hidden during all training
- For a given hyperparameter setting, learn the model parameters on training set
- Minize the loss
- Evaluate the trained model on the validation set
- Tune the hyperparameters to maximize a certain metric (e.g. accuracy)
Only generalization counts!¶
- Never evaluate your final models on the training data, except for:
- Tracking whether the optimizer converges (learning curves)
- Diagnosing under/overfitting:
- Low training and test score: underfitting
- High training score, low test score: overfitting
- Always keep a completely independent test set
- On small datasets, use multiple train-test splits to avoid sampling bias
- You could sample an 'easy' test set by accident
- E.g. Use cross-validation (see later)
Better data representations, better models¶
- Algorithm needs to correctly transform the inputs to the right outputs
- A lot depends on how we present the data to the algorithm
- Transform data to better representation (a.k.a. encoding or embedding)
- Can be done end-to-end (e.g. deep learning) or by first 'preprocessing' the data (e.g. feature selection/generation)
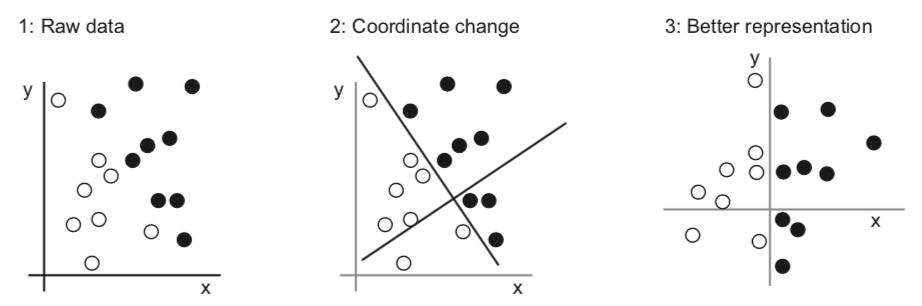
Feature engineering¶
- Most machine learning techniques require humans to build a good representation of the data
- Especially when data is naturally structured (e.g. table with meaningful columns)
- Feature engineering is often still necessary to get the best results
- Feature selection, dimensionality reduction, scaling, ...
- Applied machine learning is basically feature engineering (Andrew Ng)
- Nothing beats domain knowledge (when available) to get a good representation
- E.g. Iris data: leaf length/width separate the classes well
Build prototypes early-on
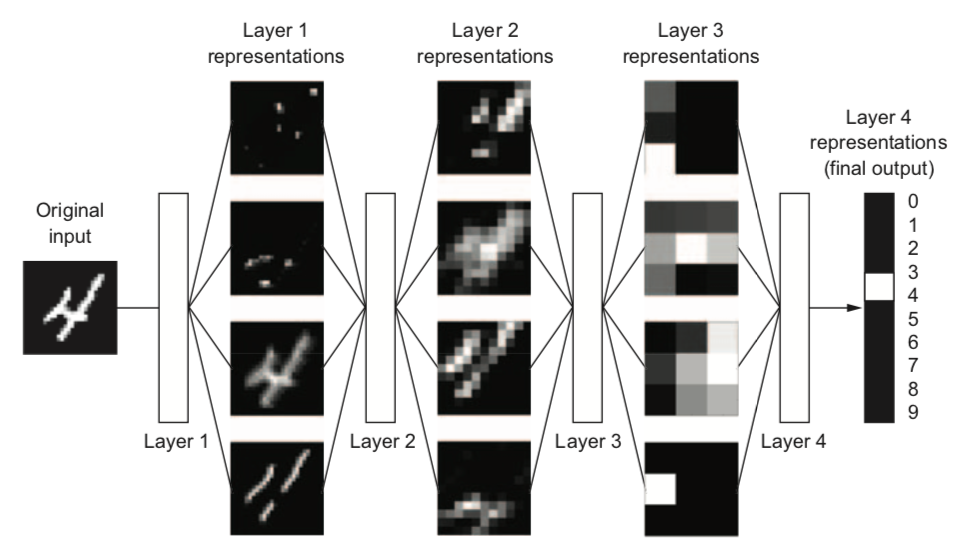
Learning data transformations end-to-end¶
- For unstructured data (e.g. images, text), it's hard to extract good features
- Deep learning: learn your own representation (embedding) of the data
- Through multiple layers of representation (e.g. layers of neurons)
- Each layer transforms the data a bit, based on what reduces the error
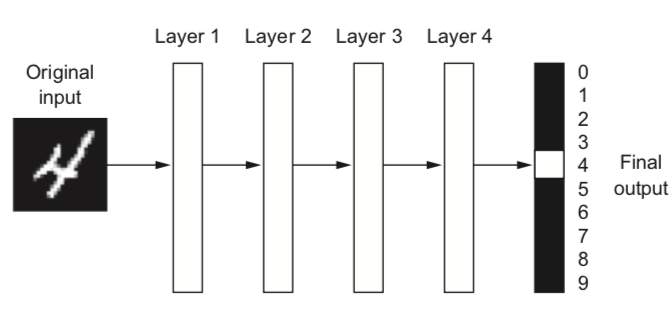
Example: digit classification¶
- Input pixels go in, each layer transforms them to an increasingly informative representation for the given task
- Often less intuitive for humans
Curse of dimensionality¶
- Just adding lots of features and letting the model figure it out doesn't work
- Our assumptions (inductive biases) often fail in high dimensions:
- Randomly sample points in an n-dimensional space (e.g. a unit hypercube)
- Almost all points become outliers at the edge of the space
- Distances between any two points will become almost identical
Practical consequences¶
- For every dimension (feature) you add, you need exponentially more data to avoid sparseness
- Affects any algorithm that is based on distances (e.g. kNN, SVM, kernel-based methods, tree-based methods,...)
- Blessing of non-uniformity: on many applications, the data lives in a very small subspace
- You can drastically improve performance by selecting features or using lower-dimensional data representations
"More data can beat a cleverer algorithm"¶
(but you need both)
- More data reduces the chance of overfitting
- Less sparse data reduces the curse of dimensionality
- Non-parametric models: number of model parameters grows with amount of data
- Tree-based techniques, k-Nearest neighbors, SVM,...
- They can learn any model given sufficient data (but can get stuck in local minima)
- Parametric (fixed size) models: fixed number of model parameters
- Linear models, Neural networks,...
- Can be given a huge number of parameters to benefit from more data
- Deep learning models can have millions of weights, learn almost any function.
- The bottleneck is moving from data to compute/scalability
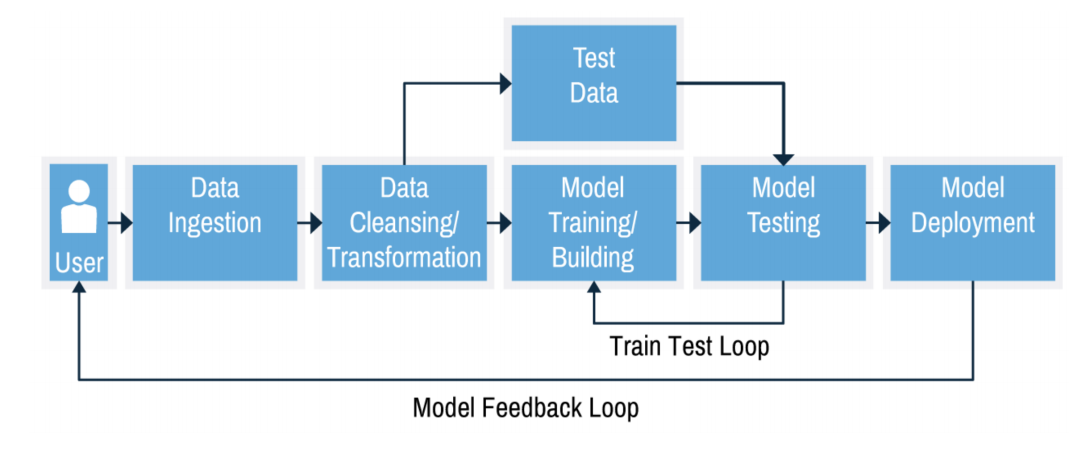
Building machine learning systems¶
A typical machine learning system has multiple components, which we will cover in upcoming lectures:
- Preprocessing: Raw data is rarely ideal for learning
- Feature scaling: bring values in same range
- Encoding: make categorical features numeric
- Discretization: make numeric features categorical
- Label imbalance correction (e.g. downsampling)
- Feature selection: remove uninteresting/correlated features
- Dimensionality reduction can also make data easier to learn
- Using pre-learned embeddings (e.g. word-to-vector, image-to-vector)
Learning and evaluation
- Every algorithm has its own biases
- No single algorithm is always best
- Model selection compares and selects the best models
- Different algorithms, different hyperparameter settings
- Split data in training, validation, and test sets
Prediction
- Final optimized model can be used for prediction
- Expected performance is performance measured on independent test set
- Together they form a workflow of pipeline
- There exist machine learning methods to automatically build and tune these pipelines
- You need to optimize pipelines continuously
- Concept drift: the phenomenon you are modelling can change over time
- Feedback: your model's predictions may change future data
Summary¶
- Learning algorithms contain 3 components:
- Representation: a model $f$ that maps input data $X$ to desired output $y$
- Contains model parameters $\theta$ that can be made to fit the data $X$
- Loss function $\mathcal{L}(f_{\theta}(X))$: measures how well the model fits the data
- Optimization technique to find the optimal $\theta$: $\underset{\theta}{\operatorname{argmin}} \mathcal{L}(f_{\theta}(X))$
- Representation: a model $f$ that maps input data $X$ to desired output $y$
Select the right model, then fit it to the data to minimize a task-specific error $\mathcal{E}$
- Inductive bias $b$: assumptions about model and hyperparameters
$\underset{\theta,b}{\operatorname{argmin}} \mathcal{E}(f_{\theta, b}(X))$
- Inductive bias $b$: assumptions about model and hyperparameters
Overfitting: model fits the training data well but not new (test) data
- Split the data into (multiple) train-validation-test splits
- Regularization: tune hyperparameters (on validation set) to simplify model
- Gather more data, or build ensembles of models
- Machine learning pipelines: preprocessing + learning + deployment